
§ 2. Поверхностные интегралы второго рода
Определение. Пусть в каждой точке двухсторонней поверхности задана функция . Выберем на поверхности сторону поверхности (верхнюю или нижнюю).
Разобьём
поверхность
сетью простых кривых на ячейки
![]() ,
которые проектируются на плоскость
в ячейки
,
которые проектируются на плоскость
в ячейки
![]() с площадями
с площадями
![]() .
Наибольший из диаметров ячейки
.
Наибольший из диаметров ячейки
![]() назовём рангом дробления и обозначим
его
.
В каждой частичной ячейке
возьмём произвольную точку
и вычислим в ней значение функции
.
Умножим
на площадь проекции ячейки
на плоскости
,
т.е. составим произведение
назовём рангом дробления и обозначим
его
.
В каждой частичной ячейке
возьмём произвольную точку
и вычислим в ней значение функции
.
Умножим
на площадь проекции ячейки
на плоскости
,
т.е. составим произведение
![]() и составим интегральную сумму для
верхней и для нижней стороны поверхности
соответственно:
и составим интегральную сумму для
верхней и для нижней стороны поверхности
соответственно:
 и
и
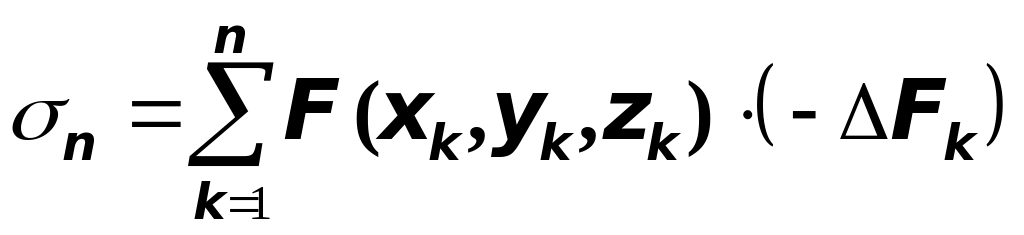 .
.
Измельчая дробление и устремляя ранг дробления к нулю, будем искать предел
.
Если
этот предел, не зависящий от способа
дробления и выбора точек
![]() ,
существует, то он называется поверхностным
интегралом второго рода
соответственно по верхней и по нижней
стороне поверхности
и обозначается
,
существует, то он называется поверхностным
интегралом второго рода
соответственно по верхней и по нижней
стороне поверхности
и обозначается
![]() .
.
Аналогично определяются
интегралы
![]() и
и
![]() ,
причём принято обозначение
,
причём принято обозначение
![]() ,
,
где все интегралы берутся по одной и той же стороне поверхности.
Свойства
поверхностных интегралов очевидно.
Отметим только, что если поверхности
представляет собой цилиндрическую
поверхность, образующие которой
перпендикулярны плоскости
,
то
![]() .
.
Это с очевидностью следует из определения поверхностного интеграла второго рода.
1. Теорема существования поверхностного интеграла второго рода
Теорема. Если двухсторонняя поверхность задана уравнением , причём и частные производные и существуют и непрерывны в простой области плоскости и если в каждой точке поверхности задана непрерывная функция , то поверхностный интеграл по верхней и нижней стороне поверхности существует и выражается через двойной интеграл для верхней стороны поверхности :
![]()
и соответственно для нижней стороны поверхности :
![]() .
.
Пример.
Вычислить
![]() по нижней стороне поверхности
,
заданной уравнением
по нижней стороне поверхности
,
заданной уравнением
![]() над областью
,
ограниченной прямыми
над областью
,
ограниченной прямыми
![]() (рис. 3).
(рис. 3).
Р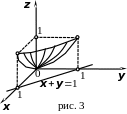 ешение.
В соответствии с теоремой существования
и принимая во внимание, что поверхностный
интеграл берётся по нижней стороне
поверхности
,
получим
ешение.
В соответствии с теоремой существования
и принимая во внимание, что поверхностный
интеграл берётся по нижней стороне
поверхности
,
получим
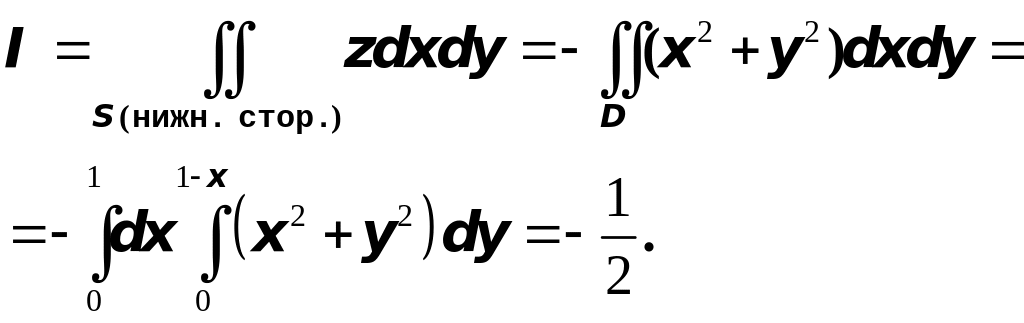 2.
Связь между поверхностными интегралами
первого и второго рода
2.
Связь между поверхностными интегралами
первого и второго рода
Будем
рассматривать поверхностные интегралы
первого и второго рода по двухсторонней
поверхности
,
нормаль к которой образует углы
,
![]() и
и
![]() соответственно с координатными осями
соответственно с координатными осями
![]() ,
,
![]() и
и
![]() .
Покажем, что
.
Покажем, что
![]() , (1)
, (1)
причём здесь через обозначен угол нормали, входящей в выбранную сторону поверхности интегрирования в интеграле, стоящем слева, с осью .
Для доказательства перейдём в интегралах, стоящих в левой и правой частях равенства (1), к двойному интегралу в силу теоремы существования, считая, что двухсторонняя поверхность задана уравнением , причём , и определены и непрерывны в простой области плоскости , тогда получим
![]() ,
,
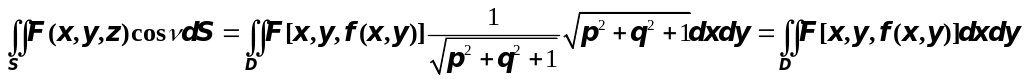 .
.
Мы видим, что правые части этих равенств совпадают, следовательно, совпадают и левые, т.е.
.
Аналогично можно доказать и такое, более общее, соотношение:
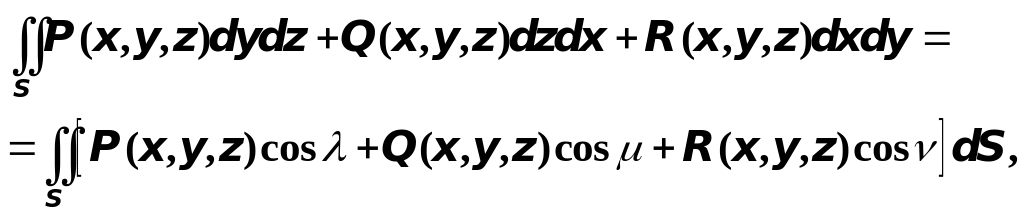
где через , и обозначены углы нормали, входящей в выбранную сторону поверхности интегрирования, в интегралы, стоящие слева, с координатными осями , и , а интегралы, стоящие в правой и левой частях равенства, существуют.
