3. Вычисление площади кривой поверхности с помощью двойного интеграла.
Рассмотрим
поверхность
,
заданную уравнением
.
Допустим, что функция
непрерывна и имеет непрерывные частные
производные
и
.
Допустим, что все три частные производные
не обращаются в ноль ни в одной точке
поверхности
,
т.е. поверхность
в каждой точке имеет касательную
плоскость. При таких предположениях в
каждой точке поверхности
существует нормаль
,
причём вектор
.
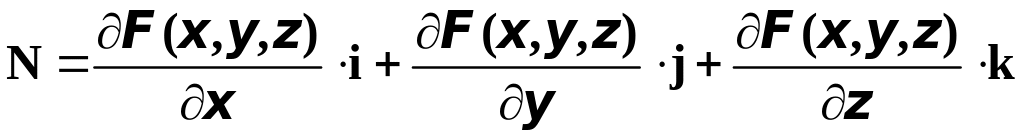Допустим, в частности, что поверхность задана уравнением . Очевидно, что мы можем считать, что
п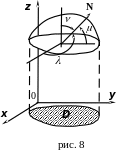
ричём
частные производные
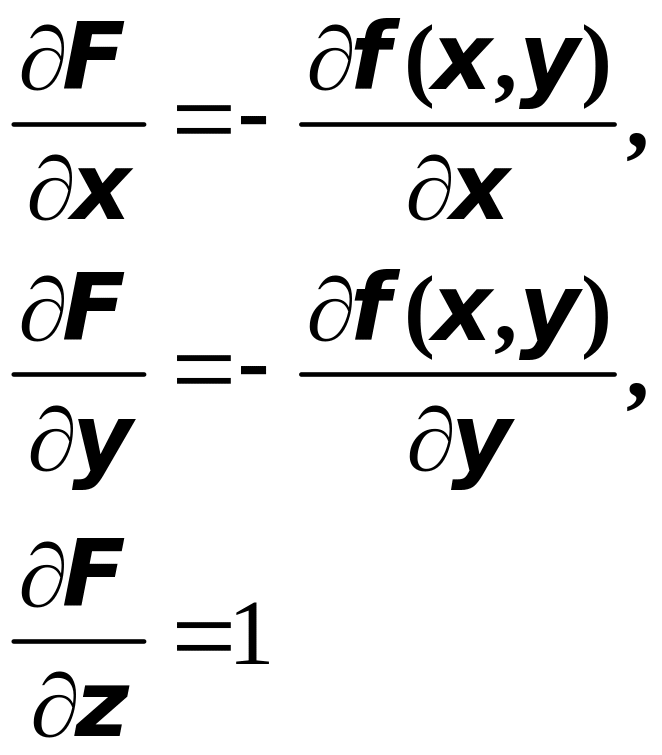
непрерывны в силу сделанных выше предположений. Обозначим
,
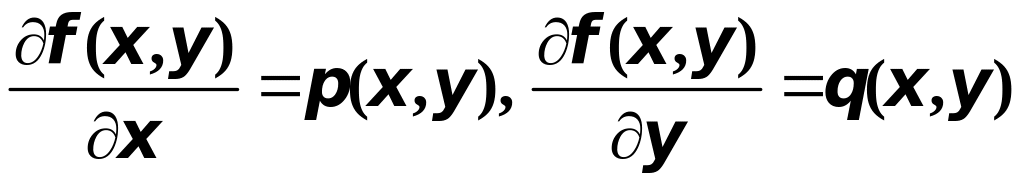тогда ясно, что нормаль к поверхности будет иметь координаты
.
Единичный вектор нормали, следовательно, имеет вид
,
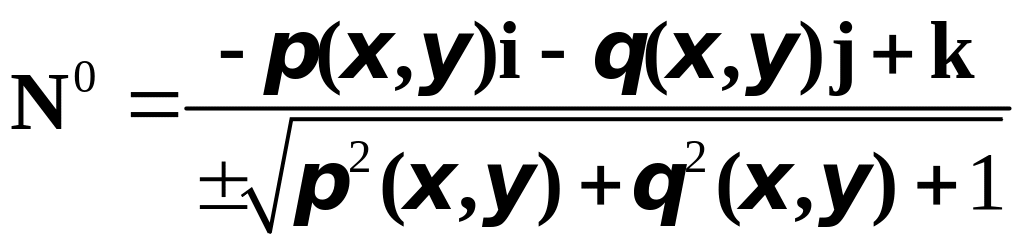где
- орты системы координат (рис. 8).
Как известно, координаты единичного
вектора совпадают с направляющими
косинусами данного вектора. Обозначим
через
и
углы нормали
соответственно с координатными осями
,
и
.
Знак
в знаменателе последней формулы означает,
что мы можем выбрать на нормали два
взаимно противоположных направления,
т.е. для направляющих косинусов нормали
получим такие формулы:
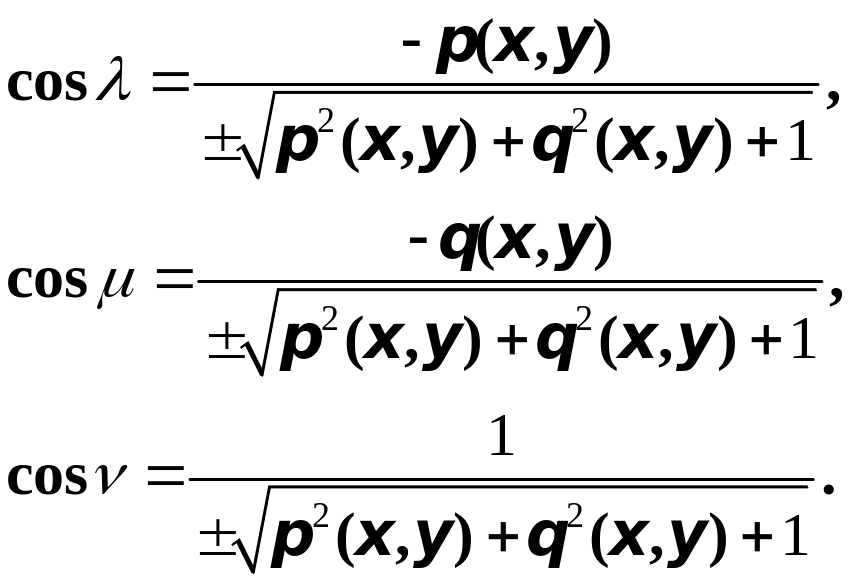
Зафиксируем на нормали то направление,
которое образует острый угол с осью
,
т.е. выберем в формулах для направляющих
косинусов такой знак перед корнем, чтобы
было
.
О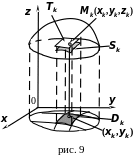
чевидно,
что следует взять плюс, причём этот знак
следует зафиксировать во всех трёх
формулах. Для получения направляющих
косинусов нормали, имеющей противоположное
направление, мы должны изменить знаки
на противоположные. Рассмотрим теперь
поверхность
,
расположенную над простой областью
,
лежащей в плоскости
(рис. 9). Разобьём область
сетью простых линий на ячейки
,
,…,
с площадями
,
,…,
,
- ранг дробления области
.
Рассмотрим цилиндрические поверхности,
образующие которых параллельны оси
,
а направляющими служит дробящая сеть
линий области
.
Эти цилиндрические поверхности переносят
дробление из области
на поверхность
,
которая разбивается таким образом на
ячейки
,
,
…,
.
Выберем в каждой ячейке
произвольную точку
и проведём через неё касательную площадку
до пересечения с вышеназванными
цилиндрическими поверхностями. Обозначим
площадь касательной площадки
через
.
Если существует конечный предел
,
не зависящий ни от способа дробления,
ни от выбора точек
на поверхности
,
то она называется площадью поверхности
,
расположенной над областью
,
а сама поверхность в этом случае
называется квадрируемой. Заметим,
что
является ортогональной проекцией
площадки
, их площади связаны соотношением
,
где
- есть острый угол между площадками
и
,
но угол между двумя плоскостями равен
углу