
1. Геометрической смысл двойного интеграла
Если
![]() в каждой точке простой области
,
по которой ведется интегрирование, то
непосредственно из определения двойного
интеграла следует (см. рис. 5), что двойной
интеграл
в каждой точке простой области
,
по которой ведется интегрирование, то
непосредственно из определения двойного
интеграла следует (см. рис. 5), что двойной
интеграл
![]() даёт нам объём тела, ограниченного снизу
областью
,
сверху - поверхностью, уравнение которой
даёт нам объём тела, ограниченного снизу
областью
,
сверху - поверхностью, уравнение которой
![]() ,
а с боков - цилиндрической поверхностью,
образующие которой параллельны оси
,
а с боков - цилиндрической поверхностью,
образующие которой параллельны оси
![]() ,
а направляющей служит граница области
(контур
),
т.е.
,
а направляющей служит граница области
(контур
),
т.е.

где
![]() - площадь область
.
- площадь область
.
Приведём без доказательства свойства 3-7, очевидно которых следует непосредственно из определения двойного интеграла:
3.
![]()
4.
![]() ,
,
где
![]() и
и
![]() - некоторые постоянные.
- некоторые постоянные.
5. Если область разбита простой кривой на две части и , то тогда
![]() .
.
6. Если в каждой точке области
:
![]() ,
то
,
то
![]() .
.
7. Если в каждой точке области
:
![]() ,
то
,
то
![]()
8. Если в каждой точке области справедливо неравенство
![]() ,
то
,
то
![]() ,
где
- площадь области
.
,
где
- площадь области
.
Доказательство. В силу свойства 7 очевидно, что
![]()
откуда следует
![]()
остаётся
учесть, что
![]() .
.
9. Теорема
о среднем. Если в каждой
точке замкнутой области
непрерывна, то тогда в области
найдётся точка
![]() такая, что
такая, что
![]() ,
,
где - площадь области .
Доказательство.
Так как функция
непрерывна в замкнутой области
,
то в ней достигает своего наименьшего
![]() и наибольшего
значения, т.е. справедливо неравенство
,
откуда в силу свойства 7 вытекает
и наибольшего
значения, т.е. справедливо неравенство
,
откуда в силу свойства 7 вытекает
.
Разделив почленно полученное соотношение на положительную величину получим
 .
.
Ввиду того, что функция непрерывна в замкнутой области , а и её наименьшее и наибольшее значение соответственно, то в области найдётся некоторая точка такая, что
 ,
,
откуда и следует, что .
Значение
![]() называют "средним" значением
функции в области
.
называют "средним" значением
функции в области
.
2. Вычисление двойного интеграла
В ычислим
двойной интеграл
в предположении, что функция
положительна в области
,
а область
ограничена снизу кривой
ычислим
двойной интеграл
в предположении, что функция
положительна в области
,
а область
ограничена снизу кривой
![]() ,
сверху кривой
,
сверху кривой
![]() (рис. 6), причём
(рис. 6), причём
![]() ;
мы предполагаем, что функции
;
мы предполагаем, что функции
![]() и
и
![]() непрерывны в промежутке
и в каждой его точке
непрерывны в промежутке
и в каждой его точке
![]() .
Из геометрического смысла двойного
интеграла ясно, что двойной интеграл
.
Из геометрического смысла двойного
интеграла ясно, что двойной интеграл
![]() даёт нам объём тела, изображенного на
рис. 6.
даёт нам объём тела, изображенного на
рис. 6.
Найдём
объём этого тела с помощью определённого
интеграла. Для этого проведём сечение
тела плоскостью
![]() .
Обозначим площадь этого сечения
.
Обозначим площадь этого сечения
![]() .
Известно, что объём тела по площадям
сечений вычисляется так:
.
Известно, что объём тела по площадям
сечений вычисляется так:
 .
.
Остаётся найти площадь сечения . Очевидно, что это сечение представляет собою криволинейную трапецию, ограниченную снизу прямой , сверху - кривой, уравнение которой (причём здесь фиксировано), а с боков - прямыми, параллельными оси .
Следовательно
 .
.
Подставляя найденное значение в исходный интеграл, окончательно получим
 .
.
Интеграл стоящий в правой части этого равенства, называется повторным или двукратным и записывается так:

Итак, окончательно получаем такое выражение двойного интеграла через повторный:
 .
.
Заметим, что интеграл
 называется внутренним, при этом говорят,
что внутреннее интегрирование ведется
по переменной
,
а внешнее - по переменной
.
называется внутренним, при этом говорят,
что внутреннее интегрирование ведется
по переменной
,
а внешнее - по переменной
.
Проводя совершенно аналогичные рассуждения, мы можем получить точно такую же форму для вычисления двойного интеграла, где внутреннее интегрирование выполнено по переменной , а внешнее - по переменной (рис. 6):
 .
.
Очевидно, не играет роли, по какой переменной нужно выполнять внутреннее интегрирование, а по какой - внешнее.
Пример. Вычислить
![]() ,
,
где область
ограничена прямыми
![]() (рис. 7).
(рис. 7).
Р ешение.
Решим пример двумя способами.
ешение.
Решим пример двумя способами.
Первый способ. Выполним внутреннее интегрирование по , а внешнее по , тогда получим
 .
.
Вычислим внутренний интеграл:
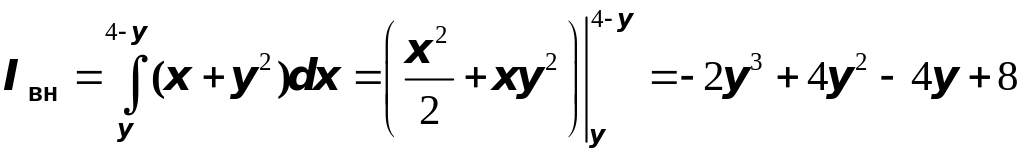 .
.
Подставляя найденное значение в выражение для , получим
 .
.
Второй способ. Внутреннее интегрирование выполним по переменной , а внешнее - по переменной . Заметим, что при этом область мы должны разбить на две области и (как указано на рис. 8), следовательно, двойной интеграл выразится в виде суммы таких двух повторных интегралов:





Итак, окончательно получим
![]() .
.
