Свойства определителей
Если какая-либо строка (столбца) матрицы состоит из одних нулей, то ее определитель равен 0.
Если все элементы какой-либо строки (столбца) матрицы умножить на число ,то ее определитель умножится на это число .
Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов.
При транспонировании матрицы ее определитель не изменяется:
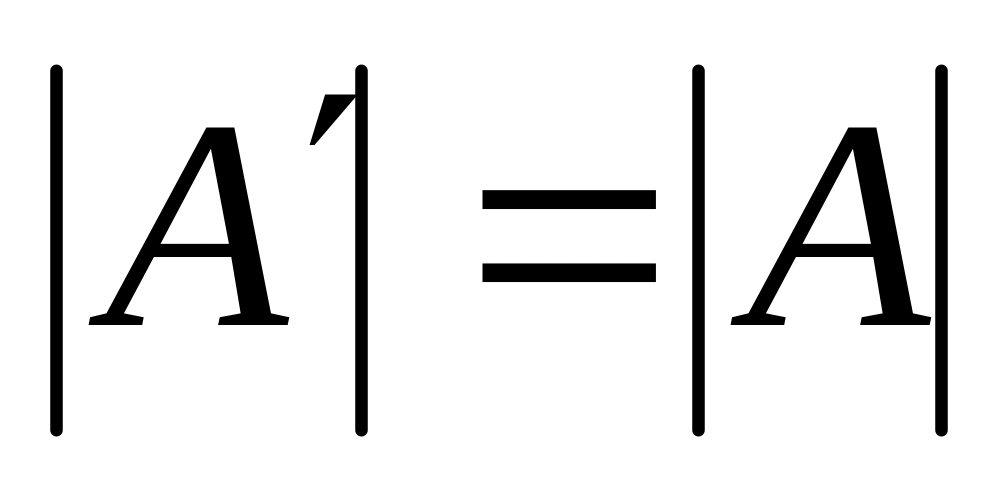.При перестановки двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.
Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Сумма произведений произвольных чисел
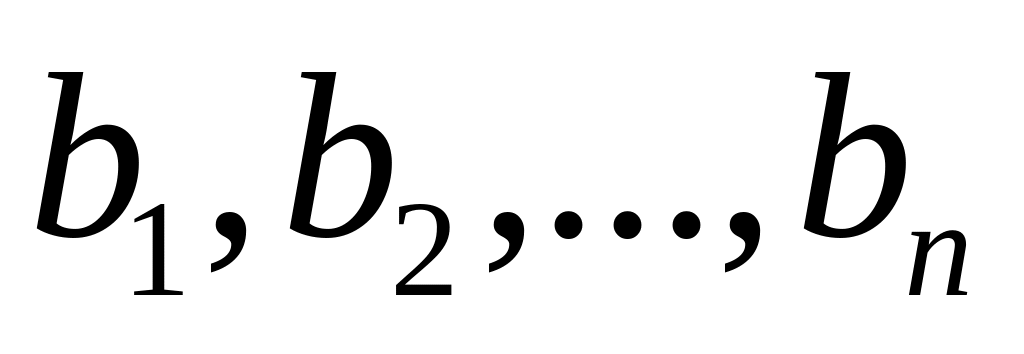на алгебраические дополнения любой
строки (столбца) равна определителю
матрицы, полученной из данной заменой
элементов этой строки (столбца) на числа
.
10.
Определитель произведения двух квадратных
матриц равен произведению их определителей:
,
где
,
а
и
- матрицы
-го
порядка.
Перечисленные свойства определителей позволяют существенно упростить их вычисления для определителей высоких порядков. При этом с помощью свойств 1-9 желательно преобразовать исходную матрицу таким образом, чтобы она имела строку (столбец), содержащую как можно больше нулей, а потом вычислить определитель, разложенный по этой строке (столбцу).
3. Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления. Обратная матрица
Для каждого числа
существует обратное число
такое, что произведение
.
Для квадратных матриц тоже вводится
аналогичное понятие.
Определение.
Матрица
называется обратной по отношению к
квадратной матрице
, если
при умножении этой матрицы на данную
как справа, так и слева получается
единичная матрица:
.
Только квадратная матрица может иметь обратную, однако не каждая квадратная матрица имеет обратную.
Определение.
Матрица
является
невырожденной
(неособенной),
если
,
в противном случае при
матрица
называется вырожденной
(особенной).
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица является невырожденной (неособенной) и вычисляется по формуле
,
где
- присоединенная матрица, состоящая из
алгебраических дополнений элементов
транспонированной матрицы, т.е.
.
Необходимость. Пусть матрица имеет обратную , т.е. . По свойству 10 определителей имеем: , т.е. и .
Достаточность. Пусть . Рассмотрим квадратную матрицу n-го порядка , называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы , транспонированной к . Тогда элементы произведения матриц определяются по правилу умножения матриц. Поэтому матрица В является диагональной, элементы ее главной диагонали равны определителю исходной матрицы. А произведение на равно той же матрице В: .
Единственность обратной матрицы. Предположим, что существуют еще матрицы и такие, что и , где матрица получена по формуле и выполняются равенства и . Тогда, умножая на слева первое из них, получаем: , откуда , т.е. . Аналогично, умножая второе равенство на справа, получаем . Единственность доказана.