
- •1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.
- •Виды матриц:
- •Операции над матрицами
- •Свойства операций сложения и умножения матриц
- •Возведение в степень.
- •Транспонирование матриц.
- •Свойства операции транспонирования.
- •2. Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца. Определители и их свойства
- •Свойства определителей
- •3. Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления. Обратная матрица
- •Алгоритм вычисления обратной матрицы.
- •Запишем систему в матричной форме:
- •Пример. Решить систему уравнений по формулам Крамера
- •5. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса.
- •Пример. Методом Гаусса решить систему:
- •Метод обратной матрицы.
- •7. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).
- •Решение системы линейных уравнений с неизвестными
- •8. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры. Понятие функции одной переменной
- •Способы задания функций:
- •Основные свойства функций
- •9. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая). Элементарная функция
- •Основные элементарные функции
- •10. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести). Уравнение линии на плоскости
- •Взаимное расположение двух линий
- •Уравнение прямой на плоскости
- •Уравнение прямой, проходящей через заданную точку в данном направлении
- •Уравнение пучка прямых Уравнение прямой в отрезках
- •Общее уравнение прямой и его исследование
- •Точка пересечения прямых
- •11. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых. Общее уравнение прямой и его исследование
- •Условия параллельности и перпендикулярности двух прямых:
- •12. Предел последовательности при и предел функции при . Признаки существования предела (с доказательством теоремы о пределе промежуточной функции). Предел числовой последовательности
- •Предел функции в бесконечности и в точке
- •Признаки существования предела
- •13. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать). Предел функции в точке
- •Основные теоремы о пределах. Признаки существования предела
- •Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.Е.
- •Предел произведения конечного числа функций равен произведению пределов этих функций, т.Е.
- •Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.Е.
- •Бесконечно большие величины
- •Свойства бесконечно больших величин
- •Связь между бесконечно малыми и бесконечно большими величинами
- •15. Второй замечательный предел, число е. Понятие о натуральных логарифмах. Второй замечательный предел.
- •16. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры. Непрерывность функции
- •Свойства функций, непрерывных в точке
- •1. Если функции и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .
- •2. Если функция непрерывна в точке и , то существует такая окрестность точки , в которой .
- •Точки разрыва функции
- •Свойства функций, непрерывных на отрезке
- •17. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке. Определение производной
- •Задача о касательной
- •18. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему). Понятие дифференцируемости функции
- •Связь между дифференцируемостью функции и ее непрерывностью
- •19. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •20. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции. Производные основных элементарных функций (таблица производных)
- •Производная сложной функции
- •21. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
- •22. Достаточные признаки монотонности функции (один из них доказать). Признаки возрастания и убывания функции.
- •23. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).
- •24. Достаточные признаки существования экстремума (доказать одну из теорем).
- •25. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.
- •26. Общая схема исследования функций и построения их графиков. Пример.
- •27. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия. Основные понятия. Частные производные
- •Частные производные функции двух переменных
- •Экстремум функции двух переменных
- •Инвариантность формы дифференциала
- •Приближенные вычисления с помощью дифференциала
- •30. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать). Понятие первообразной и неопределенный интеграл
- •Свойства неопределенного интеграла
- •31. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
- •32. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
- •Методы вычисления определенного интеграла
- •33. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
- •Геометрический смысл определенного интеграла.
- •Экономический смысл определенного интеграла.
- •Свойства определенного интеграла
- •34. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона—Лейбница. Определенный интеграл с переменным верхним пределом
- •Формула Ньютона-Лейбница.
- •35. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства). Несобственные интегралы с бесконечными пределами интегрирования
- •36. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.
О![]() пределение.
Матрицей размера
называется прямоугольная таблица,
содержащая m
строк и n
столбцов.
пределение.
Матрицей размера
называется прямоугольная таблица,
содержащая m
строк и n
столбцов.
Матрицы широко применяются для описания экономических объектов и процессов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты.
Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i - номер строки, j - номер столбца:
Виды матриц:
1) Матрица-строка: ;
2) Матрица-столбец: ; 3) Нулевая матрица: ;
4) Квадратная матрица – если (например n = 2): ;
5) Диагональная матрица (напр. 3-го порядка, где любые числа ): ;
6) Единичная матрица
(например, 3-го порядка)
![]()
Операции над матрицами
Умножение матрицы на число.
Произведением матрицы A на число называется матрица ,элементы которой для
Пример. Вычислить , если . Р е ш е н и е: .
Если
![]() ,
то
,
то
![]() (нулевая матрица того же размера).
(нулевая матрица того же размера).
Сложение матриц.
Суммой
матриц
![]() и
и
![]() одинакового размера
одинакового размера
![]() называется матрица
называется матрица
![]() ,
элементы которой
,
элементы которой
![]() для
для
Пример. Вычислить С = А + В, если . Р е ш е н и е: .
Вычитание матриц.
Разность
матриц одинакового размера определяется
как
![]() .
.
Умножение матриц.
Умножение
матрицы
на матрицу
определено, когда число столбцов первой
матрицы равно числу строк второй (условие
согласованности). Тогда произведением
матриц
![]() называется матрица
называется матрица
![]() ,
каждый элемент которой
,
каждый элемент которой
![]() равен сумме произведений элементов
равен сумме произведений элементов
![]() -ой
строки матрицы
на соответствующие элементы
-ой
строки матрицы
на соответствующие элементы
![]() -го
столбца матрицы
:
-го
столбца матрицы
:
![]() ,
где
,
где
Пример.
Вычислить
произведение матриц
![]() ,
где
,
где
![]() ,
,
![]() .
.
Р е ш е н и е.
Найдем
размер матрицы произведения
![]() ,
следовательно, умножение возможно.
,
следовательно, умножение возможно.
![]() =
=![]() .
.
Свойства операций сложения и умножения матриц
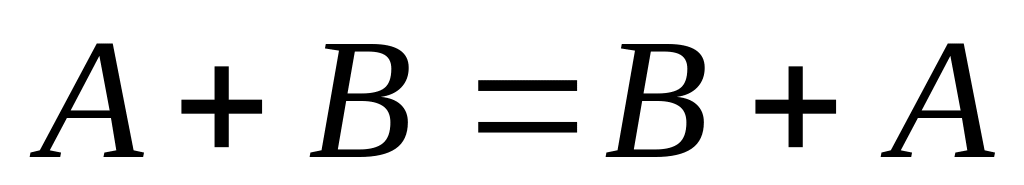 . 5)
. 5)
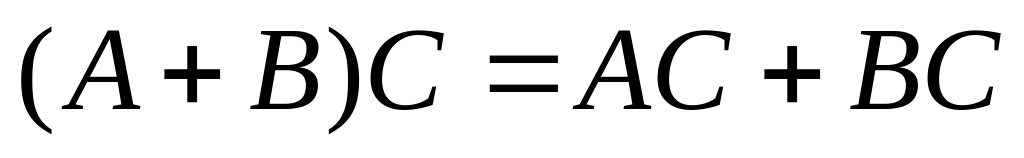 .
.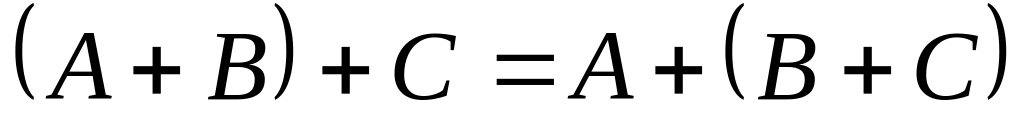 . 6)
. 6)
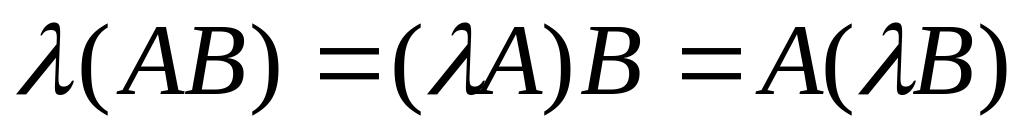 .
.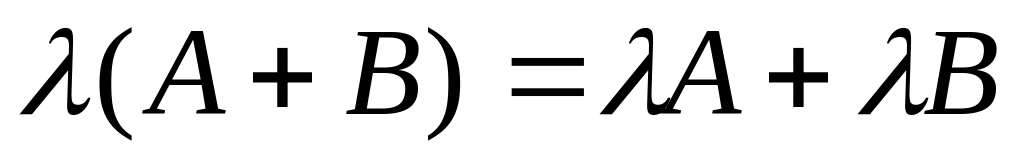 . 7)
. 7)
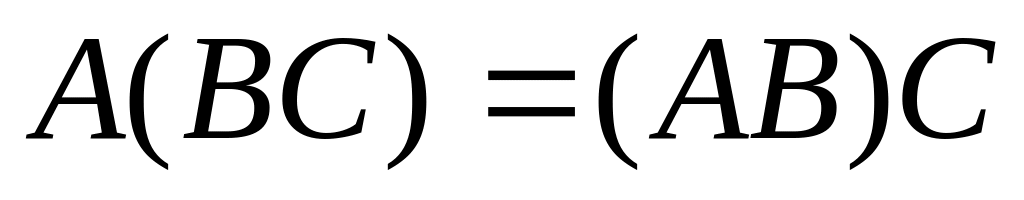 .
.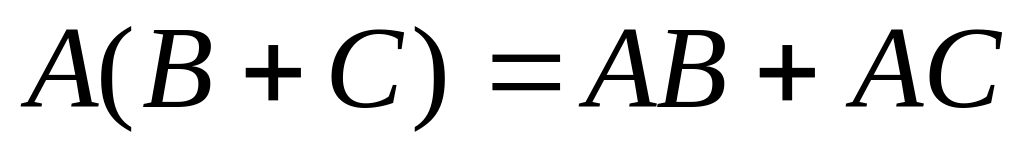 .
.
8)
![]() (в общем случае). Кроме того, если
(в общем случае). Кроме того, если
![]() существует, то
существует, то
![]() может вообще не существовать.
может вообще не существовать.
9)
![]()
![]() ,
где
,
где
![]() - единичная квадратная матрица.
- единичная квадратная матрица.
10)
Произведение двух ненулевых матриц
может равняться нулевой матрице, т.е.
если
![]() ,
то не следует, что
,
то не следует, что
![]() или
или
![]() .
.
Пример.
![]() ,
,
![]() ,
но
,
но
![]() .
.
Возведение в степень.
Целой
положительной степенью
![]() квадратной матрицы
называют
произведение
матриц, равных
,
т.е.
.
квадратной матрицы
называют
произведение
матриц, равных
,
т.е.
.
Транспонирование матриц.
Транспонирование
матрицы есть переход матрицы
к матрице
![]() ,
в которой строки и столбцы поменялись
местами с сохранением порядка.
,
в которой строки и столбцы поменялись
местами с сохранением порядка.
![]() ,
,
![]() ,
,
т.е. если
имеет размер
![]() ,
то
имеет размер
,
то
имеет размер
![]() .
.
Свойства операции транспонирования.
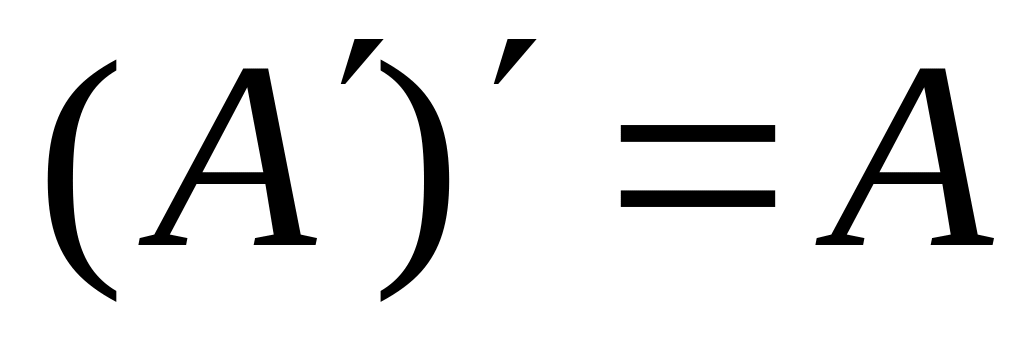 . 3)
. 3)
 .
.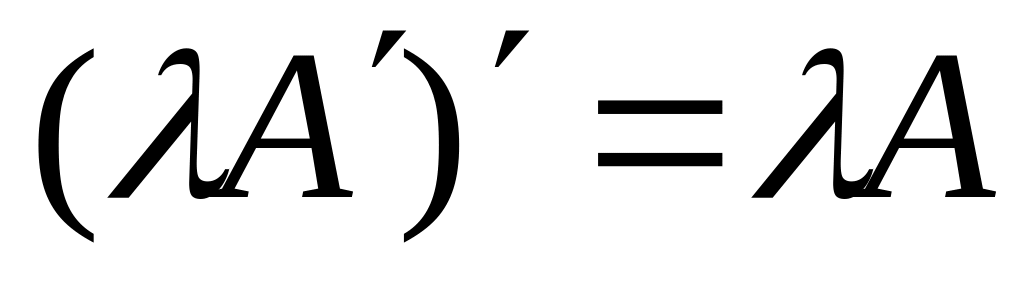 .
4)
.
4)
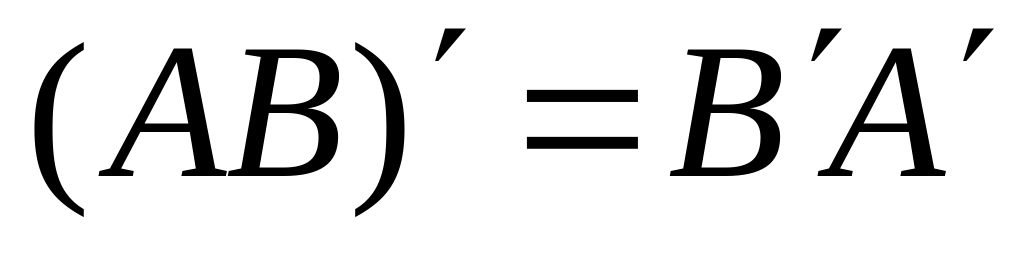 .
.
2. Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца. Определители и их свойства
Понятие определителя - число, характеризующее квадратную матрицу , необходимо для решения систем линейных алгебраических уравнений.
Определитель
матрицы
обозначают
,
![]() ,
,
![]() .
.
1)
Определителем
матицы 1-го порядка
![]() , называется элемент
:
;
, называется элемент
:
;
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
![]() .
Произведения
называются членами определителя 2-го
порядка.
.
Произведения
называются членами определителя 2-го
порядка.
Пример.
Вычислить
определитель матрицы
![]() .
Р
е ш е н и е.
.
Р
е ш е н и е.
![]() .
.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
![]() .
.
Данная формула получила название правила треугольников или правило Сарруса.
При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:
П ример.
Вычислить определитель
ример.
Вычислить определитель
![]() .
Р
е ш е н и е.
.
Р
е ш е н и е.
![]() .
.
4)
Определитель
квадратной матрицы
![]() -го
порядка
(определитель
-го
порядка).
-го
порядка
(определитель
-го
порядка).
Рассмотрим квадратную
матрицу n-го
порядка. Зачеркнем элемент матрицы,
стоящий на пересечении
-й
строки и
-го
столбца. В результате получается матрица
порядка
![]() .
Пусть дана матрица
n-го
порядка:
.
Пусть дана матрица
n-го
порядка:
![]() .
.
Минором
![]() элемента
элемента
![]() матрицы n-го
порядка называется определитель матрицы
матрицы n-го
порядка называется определитель матрицы
![]() -го
порядка, полученной из матрицы
вычеркиванием
-й
строки и
-го
столбца.
-го
порядка, полученной из матрицы
вычеркиванием
-й
строки и
-го
столбца.
Н
 апример
минором
матрицы
3-го
порядка будет:
апример
минором
матрицы
3-го
порядка будет:
Определение.
Алгебраическим дополнением
![]() элемента
матрицы
-го
порядка называется минор, взятый со
знаком
элемента
матрицы
-го
порядка называется минор, взятый со
знаком
![]() :
:
![]() .
.
Пример. Найти алгебраические дополнения всех элементов матрицы
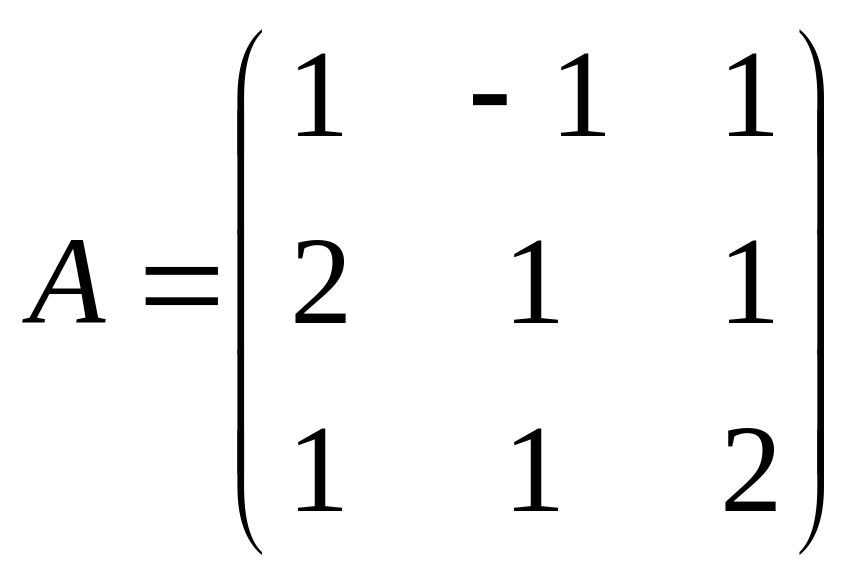 .
.
Р е ш е н и е:
|
|
|
|
|
|
|
|
|
|
|
|
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
![]() (разложение по
элементам
-й
строки;
(разложение по
элементам
-й
строки;
![]() ).
).
![]()
(разложение по
элементам
-го
столбца;
![]() ).
).
Пример. Вычислить определитель разложением по элементам
а) 1-й строки; б) 1-го столбца.
Р е ш е н и е.
а)
![]() ,
б)
,
б)
![]() .
.
