6.2 Метод послідовних наближень

Розглянемо рівняння Фредгольма

, (71)

де та неперервні.

Розв’язок шукаємо у вигляді ряду по степенях :

, (72)

де – деякі функції, які треба визначити. Для цього підставимо (72) в (71) та прирівняємо коефіцієнти при однакових степенях . Одержуємо

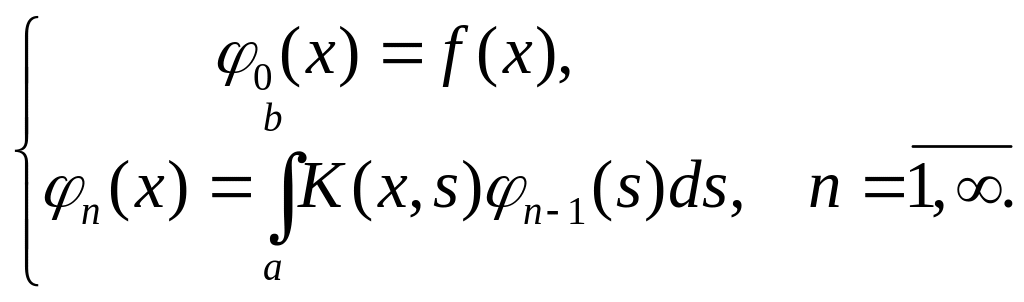(73)

Тобто (73) дає рекурентні співвідношення для послідовного обчислення всіх через та .

Зробимо оцінку зверху для . Припустимо, що та для , . Тоді , . А далі за індукцією (перевірте самостійно) . Таким чином, рівномірна збіжність ряду (72) буде забезпечена, коли

, (74)

і ряд (72) дає точний розв’язок рівняння (71) за умови (74).

У якості наближеного розв’язку рівняння (71) можна взяти скінчену кількість членів ряду, тобто

. (75)

Межу абсолютної похибки такого наближення дає наступне співвідношення

. (76)

Приклад 1. Методом послідовних наближень відшукати розв’язок рівняння

, .

Тут , . Беремо . Тоді наближений розв’язок згідно (75) має вигляд

.

Маємо

, ,

і, таким чином,

.

Тому, що в цьому прикладі

, ,

згідно (74) робимо висновок, що ряд (72) збігається при

.

Якщо взяти , то згідно (76) робимо висновок, що абсолютна похибка одержаного наближення не перевищує

.

Розглянемо тепер рівняння Вольтерра другого роду

, (77)

де .

Аналогічно попередньому шукаємо розв’язок рівняння у вигляді ряду по степенях :

(78)

Після підставлення (78) в (77) та прирівнення коефіцієнтів при однакових степенях одержуємо аналог (73)

,

, . (79)

Оцінка дає

,

,

А далі за індукцією

;

тут як і раніш

при ,

та

при .

Таким чином, ряд (78) мажорується збіжним рядом

і за ознакою Вейєрштрасса³ рівномірно збігається для довільного та дає єдиний розв’язок рівняння (77).

Наближений розв’язок задається скінченою сумою

(80)

Межу абсолютної похибки одержимо з нерівності

. (81)

Можна дати більш грубу, але більш просту оцінку похибки. Якщо в попередній нерівності винести за дужки спільний множник , то можна одержати

Ряд у фігурних дужках мажорується рядом

Тоді одержується оцінка

, (82)

при цьому необхідно, щоб було настільки велике, аби виконувалася умова

.

Приклад 2. Розв’язати інтегральне рівняння

,

взяти , .

Тут , , .

Наближений розв’язок шукаємо у вигляді

.

Інтегрування за формулами (79) дає:

;

;

;

;

.

Звідси

.

Перевірте самостійно, що точним розв’язком цього рівняння є . Порівняння його з наближеним в точках та дає:

, ,

, .

Порівняйте самостійно точний розв’язок з наближеним у вибраних вами проміжних точках відрізку [0,1].

Ясно, що головним недоліком методу послідовних наближень при розв’язанні інтегральних рівнянь є необхідність точного інтегрування в (73) або (79).

6.3 Метод квадратур

Інша найпростіша ідея розв’язання рівнянь (66), (70), це заміна інтегралів квадратурними формулами з вузлами та зведення задачі до розв’язання системи лінійних алгебраїчних рівнянь відносно наближених розв’язків в цих вузлах.

Нагадаємо деякі формули числового інтегрування з рівновіддаленими вузлами в конкретній ситуації розв’язання інтегральних рівнянь.

Розіб’ємо відрізок на частин з вузлами , , …, , де . Наближений розв’язок інтегрального рівняння у вузлах будемо позначати .

Тоді для ускладненої формули трапецій будемо мати

. (83)

Якщо взяти , , , то за ускладненою формулою Сімпсона (парабол) маємо

.

Далі, якщо взяти в тих же вузлах, що і , та підставити ту чи іншу квадратурну формулу в (66) або (70), то можна одержати систему лінійних алгебраїчних рівнянь відносно наближених значень . Так, наприклад, підставляючи (83) в (66) будемо мати систему

, .

Якщо визначник цієї системи не дорівнює нулеві ( а це треба перевіряти), то застосовуючи, наприклад, метод Гаусса з вибором головного елементу, одержуємо наближені значення , . Наближені значення в проміжних точках можна одержати, якщо побудувати, наприклад, інтерполяційний кубічний сплайн.