Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Метода_МКЕ_укр

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

447.06 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ НТУУ «КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ» ТЕПЛОЕНЕРГЕТИЧНИЙ ФАКУЛЬТЕТ

КАФЕДРА АПЕПС

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

З ДИСЦИПЛІНИ

„ОСНОВИ ТЕПЛОТЕХНІКИ”

ДЛЯ СТУДЕНТІВ СПЕЦІАЛЬНОСТІ

«ІНФОРМАЦІЙНІ ТЕХНОЛОГІЇ ПРОЕКТУВАННЯ»

РОЗРАХУНОК ДВОВИМІРНОГО СТАЦІОНАРНОГО

ТЕМПЕРАТУРНОГО ПОЛЯ

МЕТОДОМ СКІНЧЕННИХ ЕЛЕМЕНТІВ

Укладачі Молодід О.К.,

Кузьменко І.М.,

Крячок О.С.

Затверджено каф. АПЕПС протокол №8 від 21-03-2012

Київ 2012

ЗМІСТ

ВСТУП ................................................................................................................................................		3
1.	ПОНЯТТЯ ЛІНІЙНИХ ІНТЕРПОЛЯЦІЙНИХ ПОЛІНОМІВ...................................................	3
2.	ПОБУДОВА ЛІНІЙНИХ ІНТЕРПОЛЯЦІЙНИХ ПОЛІНОМІВ................................................	6
3.	ОДНОВИМІРНА ЗАДАЧА ТЕПЛОПРОВІДНОСТІ..................................................................	8
4.	ДВОВИМІРНА ЗАДАЧА ТЕПЛОПРОВІДНОСТІ...................................................................	10
5.	ПРОГРАМНА РЕАЛІЗАЦІЯ МЕТОДУ РОЗРАХУНКУ ТЕМПЕРАТУРНОГО ПОЛЯ .......	13
6.	ФОРМУВАННЯ СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ ................................	14
7.	ПРИКЛАД ПРОГРАМНОЇ РЕАЛІЗАЦІЇ МЕТОДУ ДЛЯ РОЗРАХУНКУ
ТЕМПЕРАТУРНОГО ПОЛЯ ..........................................................................................................		15
8. ІНДИВІДУАЛЬНІ ЗАВДАННЯ..................................................................................................		17
СПИСОК ЛІТЕРАТУРИ..................................................................................................................		20

ВСТУП

Розрахунок стаціонарного температурного поля, що входить до методу визначення коефіцієнту тепловіддачі – одна з важливих теплотехнічних задач. Для тіл простої форми розрахунок стаціонарного температурного поля отримується з рівняння теплопровідності за певних граничних умов. Однак, більшість тіл мають складну форму і обрахунок температурного поля в них виконується наближено за чисельними методами. Одним з таких є метод скінченних елементів (МСЕ) описаний нижче [1-4].

МСЕ базується на ідеї апроксимації безперервної функції, що описує температуру, тиск, переміщення і т.д., дискретною моделлю. Модель будується на множині кусочно-безперервних функцій, визначених на скінченній кількості підобластей, названих скінченними елементами. Тобто, складна геометрична форма розбивається на елементи таким чином, щоб на кожному з них невідома функція апроксимувалася поліномом. Причому ці поліноми мають задовольняти граничним умовам задачі та умовам безперервності функції.

У даній роботі розглянуто кілька прикладів розрахунку температурного поля за алгоритмом МСЕ, заснованим на процедурі мінімізації функціоналу, що відповідає розв'язуваній безперервній задачі [1]. У результаті виконання зазначеної процедури відбувається заміщення рівняння у частинних похідних системою лінійних рівнянь. Ці рівняння мають у якості коефіцієнтів апроксимуючі функції, які є значеннями шуканої функції.

1. ПОНЯТТЯ ЛІНІЙНИХ ІНТЕРПОЛЯЦІЙНИХ ПОЛІНОМІВ

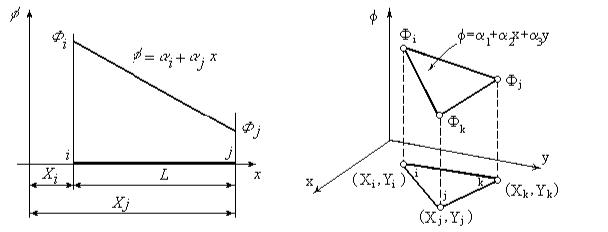
Розглянемо особливості побудови лінійних інтерполяційних поліномів, що відповідають симплекс-елементам [4]. На рисунку 1.1 зображено -

а)

б)

Рис. 1.1. Одновимірний (а) і двовимірний (б) симплекс-елементи

одновимірний симплекс-елемент (рис.1.1. а), що представляє собою прямолінійний відрізок довжини L із двома вузлами. Двовимірний симплекс-

елемент (рис.1.1. б) – трикутник із прямолінійними сторонами та трьома вузлами в кожній вершині. У двовимірному випадку лінійний інтерполяційний

поліном для симплекс-елемента має

вигляд

[2]:

1 2 x 3 y . (В

одновимірному випадку y 0 .)

За умови, що значення полінома у вузлах елемента i, j, k

відповідають значенням функції i

в цих вузлах, отримаємо систему

лінійних алгебраїчних рівнянь з невідомими C . Або в розгорнутому

вигляді

(1.1)

x j

y j

1 x

Визначимо невідомі коефіцієнти

полінома 1 , 2 ,

за допомогою відомих

значень шуканої функції у вузлових

точках

P i , j , k з розв'язку

матричного рівняння С( 1) . Тут С ( 1)

– матриця, обернена до C .Запишемо в

розгорнутому вигляді

			a
	1		i
	2		b
	2		i
			c
	3		i

a j				i
a j		ak		i
						(1.2)
bj		bk j				(1.2)
bj		bk j
c	j	c
	j		k		k

Об'єднавши											в		матрицю							В		множники										при						в	інтерполяційній							формулі
	B 1, x, y						одержимо матрицю так званих функцій форми (базисних функцій),
що обчислюється як N B C ( 1) . Якщо i,																																j,			k 1,			2,	3 , відповідно
	N [												X 2Y3 Y2 X 3																									x(Y3 Y2 )
	N [				X Y Y X						3	X Y Y X							3	X Y Y X								2		X		Y Y X					3	X Y Y X				3	X Y Y X			2
					2	3			2		3		1	3			1		3			1	2		1			2			2		3		2		3	1	3		1	3	1	2	1	2
										y( X 3 X 2 )																,
		X		Y Y X					3	X Y Y X							3	X Y Y X							2	,
			2		3	2			3			1	3	1			3			1	2		1		2
										X1Y3 Y1 X 3																										x(Y3 Y1 )
	X Y Y X						3	X Y Y X							3	X Y Y X								2			X Y Y X							3	X Y Y X					3	X Y Y X				2
2			3			2	3				1	3		1	3				1	2		1		2				2	3			2		3			1	3	1	3		1	2	1	2
										y( X 3 X1 )																,
		X		Y Y X					3	X Y Y X							3	X Y Y X							2	,
			2		3	2			3			1	3	1			3			1	2		1		2
										X1Y2 Y1 X 2																										x(Y2 Y1 )
	X Y Y X						3	X Y Y X							3	X Y Y X								2			X Y Y X							3	X Y Y X					3	X Y Y X				2
2			3			2	3				1	3		1	3				1	2		1		2				2	3			2		3			1	3	1	3		1	2	1	2
										y( X 2 X1 )																]
		X		Y Y X					3	X Y Y X							3	X Y Y X							2	]
			2		3	2			3			1	3	1			3			1	2		1		2

Тоді інтерполяційний поліном для шуканої функції може бути отриманий наступною операцією

N P

(1.3)

(										X 2Y3 Y2 X 3																						x(Y3 Y2 )
(			X	2	Y Y X			3	X Y Y X						3	X Y Y X							2			X Y Y X				3	X Y Y X					3	X Y Y X					2
				2	3		2	3		1		3		1	3			1	2		1		2		2		3		2	3		1	3		1	3			1	2	1	2
								y( X			3 X 2 )											) 1
		X 2Y3		Y2 X 3 X1Y3							Y1 X 3 X1Y2 Y1 X										2	) 1
		X 2Y3		Y2 X 3 X1Y3							Y1 X 3 X1Y2 Y1 X										2
(							X1Y3 Y1 X 3																							x(Y3 Y1 )
(	X Y Y X					3	X Y Y X						3	X Y Y X						2			X	2	Y Y X			3	X Y Y X					3	X Y Y X						2
2			3		2	3			1	3		1	3			1	2		1	2				2	3		2	3			1	3	1	3			1	2		1	2
								y( X			3 X1 )											) 2
		X 2Y3		Y2 X 3 X1Y3							Y1 X 3 X1Y2 Y1 X										2	) 2
		X 2Y3		Y2 X 3 X1Y3							Y1 X 3 X1Y2 Y1 X										2
(							X1Y2 Y1 X 2																							x(Y2 Y1 )
(	X Y Y X					3	X Y Y X						3	X Y Y X						2			X	2	Y Y X			3	X Y Y X					3	X Y Y X						2
2			3		2	3			1	3		1	3			1	2		1	2				2	3		2	3			1	3	1	3			1	2		1	2
								y( X			2 X1 )											) 3
		X 2Y3		Y2 X 3 X1Y3							Y1 X 3 X1Y2 Y1 X										2	) 3
		X 2Y3		Y2 X 3 X1Y3							Y1 X 3 X1Y2 Y1 X										2

Наприклад, функція має значення P 40,34,26 в точках відповідно за X 1,0,2 та Y [2,0,0] . Тоді, матриця C

1		1	2
C 1		0	0

1		2	0
				.
Перемножуючи вектор на обернену матрицю отримуємо
N [	1	y,1		1	x	1	y,		1	x	1	y]
N [	2	y,1	2		x	4	y,	2		x	4	y]
	2		2			4		2			4
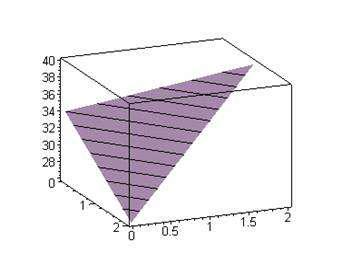
За	формулою							(1.3)				34 4x 5y . Отримане рівняння площини, як

апроксимуючої функції, відображене графічно

Рис. 1.2. Рівняння апроксимуючої площини.

Наприклад, у точці з координатами (1, 0.5) маємо значення функції 32.5 .

2. ПОБУДОВА ЛІНІЙНИХ ІНТЕРПОЛЯЦІЙНИХ ПОЛІНОМІВ

Апроксимуємо всю область поліномами на основі відомих точок. У загальному вигляді інтерполяційний поліном, отриманий за формулою (1.3) має вид Ni i , де i – індекс, що вказує на певний елемент.

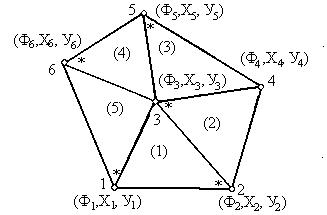
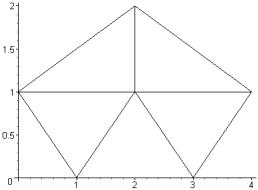
Включення двовимірного елемента в область проілюструємо на прикладі області п’ятикутної форми (рисунок 2.1)

Рис. 2.1. Тріангуляція області п’ятикутної форми
Припустимо, що в	шести	вузлах з координатами X 1,3,2,4,2,0	і
Y 0,0,1,1,2,1 функція має	значення	2.5,3,3,2,3.5,3 . Розіб’ємо форму на	5

елементів. Кожен з елементів описується трьома крайніми точками, що характеризуються координатами x, y і значенням функції в точці . Складемо масив, що характеризує всю п’ятикутну форму. Кожна строчка масиву містить координати x, y кожного з елементів та відповідні їм значенням функції при обході елементу, починаючи з певного вузла проти годинникової стрілки



	1	0	3	0	2	1	2.5	3	3
	1	0	3	0	2	1	2.5	3	3
G	2	1	3	0	4	1	3.0	3	2

2		2	2	1	4	1	3.5	3	2
0		1	2	1	2	2	3.0	3	3.5

1		0	2	1	0	1	2.5	3	3

Задамо вектор коефіцієнтів B ( для обчислення базисних функцій) і вектор , у якім будуть накопичуватися поліноми, що апроксимують безперервну функцію усередині кожного елемента. Оформимо цикл матричних обчислень для 5 елементів схематично.

1,2,3,4,5

1 G(i,1)		G(i,2)
C 1	G(i,3)	G(i,4)

1	G(i,5)	G(i,6)

N B inverse C

P[G(i,7), G(i,8), G(i,9)]

(i) N P

(*)

Рис. 2.2. Схема обрахунку апроксимуючих поліномів для складної форми.

Наприклад, для i =1 отримано

1	1	0
C 1	3	0	, N [1.5 0.5x 0.5y,	0.5 0.5x 0.5y	y], P [2.5, 3, 3] ,

1	2	1

2.25 0.25x 0.25y .

У кінцевому результаті, вектор п'яти поліномів для п'яти елементів має вид

2.25 0.25x 0.25 y,4.5 0.5x 0.5y,3.5 0.5x 0.5y,2.5 0.5y,2.5 0.5y , що графічно

зображений на рисунку 2.3.

Рис. 2.3. Апроксимація області п’ятьма поліномами

3. ОДНОВИМІРНА ЗАДАЧА ТЕПЛОПРОВІДНОСТІ

Одновимірний розподіл температур розглянемо на прикладі стрижня з теплоізольованою бічною поверхнею (рис. 3.1). У варіаційнім обчисленні встановлено, що для мінімізації функціонала

		2
K		T x		1 T Tw	2
	x
			dV qT			dS
		2		2

необхідно, щоб задовольнялося диференційне рівняння

	2
K			T x	0
		2
	x

(3.1)

(3.2)

з граничними умовами


K		T x	q T Tw 0 .	(3.3)
	x

У формулах (3.1-3.3) T – температура, K – коефіцієнт теплопровідності, q – тепловий потік заданої інтенсивності, – коефіцієнт конвективного теплообміну, Tw – температура навколишнього середовища, V – об'єм стрижня, S – площа поперечного перерізу стрижня, x – координата уздовж осі стрижня.

Таким чином, будь-який розподілT (x) , при якім функціонал (3.1) стає мінімальним, є розв'язком вихідної задачі теплопровідності (3.2-3.3).

Рис.1. Геометрія круглого стрижня

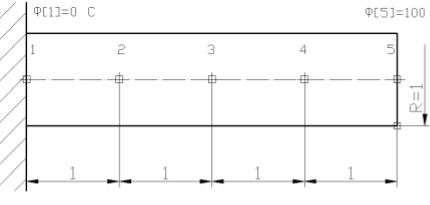
Розглянемо приклад, одновимірного потоку тепла в стрижні з теплоізольованою бічною поверхнею (рис. 3.1).

Представимо стрижень дискретною моделлю, що містить п'ять вузлових точок m , m 1...5 з координатами X 1,2,3,4,5 . Площа поперечного перерізу

стрижня A . Коефіцієнт теплопровідності сталий і рівний K i 1 Вт/м/К. У

граничних точках відомі значення температури [1] 0 , [5] 100 С.
	Сформуємо допоміжну матрицю даних G, розмірністю m 1 рядків і 11
стовпчиків G[4,		11]. При формуванні врахуємо, що qi i Twi 0 .
	Формування матриці проводимо по строках. При цьому для першого
рядка маємо
G[1,	1] X [1] , G[1,	2] X [2] , G[1,	3] [1] , G[1,	4] [2] , G[1,	5] q[1] , G[1,	6] q[2] ,
G[1,	7] [1], G[1,	8] [2] , G[1,	9] Tw[1] , G[1,	10] Tw[2] , G[1,	11] K[1] .

В цілому отримуємо

	1	2	0	[2]	1
G	2	3	[2]	[3]	1
	3	4	[3]	[4]	1
	4	5	[4]	100	1

За граничних умов другого роду при контакті з навколишнім середовищем задається температура середовища Tw.

У даному випадку – граничні умови першого роду і Tw[i]=0, коефіцієнти тепловіддачі навколишнього середовища [i]=0. Також можна ввести різний коефіцієнт теплопровідності на окремих елементах.

Для кожного з i окремих елементів обчислюємо інтерполяційні поліноми та функціонали. При обрахунку інтерполяційних поліномів і функціоналів використовуємо схему обрахунку (*), наведену вище.

В результаті, для першого елементу маємо

1	1	, B 1	x , N [2 x	1 x] ,	P [0,	[2]] .
C
1	2

Отримуємо функціонал [1] ( 1 x) [2] . Відповідно до формули (3.1)

	K			2	1	2
отримуємо [1]			[1]	A			[2] .
отримуємо [1]		x	[1]	A			[2] .
	2	x			2

Аналогічно для точок 2-4

[2] (3 x) [2] ( 2 x) [3], [2] 12 [2] [3] 2 ,[3] (4 x) [3] ( 3 x) [4] , [3] 12 [3] [4] 2 ,

	[4] (5 x) [4] 400 100 x , [4]					1	[4] 100 2 .
	[4] (5 x) [4] 400 100 x , [4]						[4] 100 2 .
					2
Маємо сумарний функціонал
	[i] 2 [2] [2] [3] 2 [3] [4] 2 [4] 100 2
		i
	Похідні від сумарного функціоналу по кожній з функцій прирівнюємо
нулю			0	для пошуку мінімуму функціоналу, відповідно до рівняння (3.2).

		[i]
	Отримуємо систему трьох лінійних алгебраїчних рівнянь з трьома
невідомими [2],					[3], [4]
			0	[2] ( [2] [3]) 0 ,

		[2]
		[2]
			0	( [2] [3]) ( [3] [4]) 0 ,

		[3]
		[3]
			0	( [3] [4]) ( [4] 100) 0

		[4]
		[4]
	Розв'язавши				систему, наприклад методом Гауса [5], отримуємо
[2] 25 , [3] 50 ,					[4] 75 .

Аналітичний розв'язок [6] задачі приводить до лінійної функції T aX b , що підтверджує отриманий вище результат.

4. ДВОВИМІРНА ЗАДАЧА ТЕПЛОПРОВІДНОСТІ

Розглянемо задачу теплопровідності у двовимірній постановці. З варіаційної точки зору відшукання мінімуму функціонала

T x, y

1 K

T x, y

2QT x, y

1 T x, y Tw

dV qT x, y

dS (4.1)

еквівалентно розв'язку диференціального рівняння теплопровідності

T x, y

(4.2)

з граничними умовами

q T

Tw 0 ,

T x, y l

(4.3)

x, y

де T – температура, K – коефіцієнт теплопровідності, q – тепловий потік заданої інтенсивності, Q – внутрішнє джерело тепла, – коефіцієнт конвективного теплообміну, Tw – температура навколишнього середовища, l – напрямні косинуси вектора нормалі до поверхні, V – об'єм, S – площа поверхні, x, y – координати.

Таким чином, будь-який розподіл T x, y , за якого функціонал (4.1) є мінімальним, буде розв'язком задачі теплопровідності (4.2-4.3).

Розглянемо приклад розрахунку двовимірного температурного поля за граничних умов першого роду в області, що приведена на рис. 2.1.

Як вказано в розділі 2, для шести вузлових точок m 6 і числа елементів

n 5 , координати вузлових точок X 1,3,2,4,2,0 , Y 0,0,1,1,2,1 .

Геометрію кожного з елементів опишемо номерами вузлів проти годинникової стрілки, починаючи з вузла, позначеного на рис. 2.1 зірочкою.

2	3	1

3	2	4
G1 5	3	4
6	3	5

1	3	6

Тріангуляція області в декартових координатах показана на рис. 4.1.

Рис. 4.1.Тріангуляція області

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.2019444.93 Кб5Метод_рек_Муратова.doc
#
12.05.2015982.53 Кб27метод_указ_программирование_вариант_2014.doc
#
27.04.20193.84 Mб1Метода УМНК (ч.2).doc
#
12.05.2015569.86 Кб13метода.ГОМ самостійна .doc
#
09.11.201992.56 Кб1Метода1 оригинал.docx
#
12.05.2015447.06 Кб3Метода_МКЕ_укр.pdf
#
09.11.2019329.22 Кб7метода_чис_мет_1.doc
#
08.08.2019624.13 Кб2метода_чис_мет_2.doc
#
12.05.20153.51 Mб9методаОПММ_27.09.07_+_СОПРОМАТ+ОПММ.pdf
#
28.04.20192.64 Mб17Методи розвязання (методичка 1).doc
#
28.04.20192.2 Mб5Методи розв’язання диференційних рівнянь з част....doc



	1	0	3	0	2	1	2.5	3	3
	1	0	3	0	2	1	2.5	3	3
G	2	1	3	0	4	1	3.0	3	2

2		2	2	1	4	1	3.5	3	2
0		1	2	1	2	2	3.0	3	3.5

1		0	2	1	0	1	2.5	3	3



	1	0	3	0	2	1	2.5	3	3
	1	0	3	0	2	1	2.5	3	3
G	2	1	3	0	4	1	3.0	3	2

2		2	2	1	4	1	3.5	3	2
0		1	2	1	2	2	3.0	3	3.5

1		0	2	1	0	1	2.5	3	3



	1	0	3	0	2	1	2.5	3	3
	1	0	3	0	2	1	2.5	3	3
G	2	1	3	0	4	1	3.0	3	2

2		2	2	1	4	1	3.5	3	2
0		1	2	1	2	2	3.0	3	3.5

1		0	2	1	0	1	2.5	3	3