ЗМІСТ

1 ЗАДАЧА КОШІ ДЛЯ ЛІНІЙНОГО РІВНЯННЯ З ЧАСТИННИМИ ПОХІДНИМИ ПЕРШОГО ПОРЯДКУ 4

1.1 Постановка задачі 4

1.2 Сітки 4

1.3 Різницева схема 6

1.4 Обчислювальний алгоритм 7

2 АПРОКСИМАЦІЯ, СТІЙКІСТЬ, ЗБІЖНІСТЬ 7

3 ЗБІЖНІСТЬ РОЗВ’ЯЗКУ РІЗНИЦЕВОЇ СХЕМИ ДО РОЗВ’ЯЗКУ ЗАДАЧІ КОШІ ДЛЯ ЛІНІЙНОГО РІВНЯННЯ З ЧАСТИННИМИ ПОХІДНИМИ ПЕРШОГО ПОРЯДКУ 12

3.1 Апроксимація 12

3.2 Стійкість 13

3.3 Збіжність 14

4 МІШАНА ЗАДАЧА ДЛЯ РІВНЯННЯ ТЕПЛОПРОВІДНОСТІ 15

4.1 Постановка задачі 15

4.2 Сітки й норми 16

4.3 Різницева схема 16

4.4 Обчислювальний алгоритм 17

4.5 Апроксимація 18

4.6 Стійкість і збіжність 19

5 ХВИЛЬОВЕ РІВНЯННЯ 20

5.1 Різницева схема 21

5.2 Стійкість і збіжність 22

6 ДЕЯКІ ЧИСЛОВІ МЕТОДИ РОЗВ’ЯЗАННЯ ІНТЕГРАЛЬНИХ РІВНЯНЬ 23

6.1 Основні означення та деякі результати теорії 23

6.2 Метод послідовних наближень 25

6.3 Метод квадратур 30

7 ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ 32

7.1 Завдання 1 32

7.2 Завдання 2. 36

7.3 Завдання 3. 37

7.4 Завдання 4. 38

7.5 Вимоги до звіту з самостійної роботи 39

ЛІТЕРАТУРА 40

1 Задача коші для лінійного рівняння з частинними похідними першого порядку

Основні ідеї сіткових (або різницевих) методів розв'язання диференційних рівнянь зручно вивчати спочатку на простих прикладах, один з яких буде розглянутий нижче.

1.1 Постановка задачі

Необхідно знайти неперервну в смузі функцію , що задовольняє при лінійному диференційному рівнянню з частинними похідними

(1)

а при початковій умові

, (2)

де - числа, - двічі неперервно диференційовна функція на всій осі, що також будемо позначати , причому передбачається

. (3)

Можна перевірити, що точним розв'язком задачі Коші (1), (2) є

. (4)

Дійсно,

і, відповідно, (1) виконується. Виконання початкової умови (2) очевидне.

Хоча розв'язок задачі Коші (1),(2) відомий, тим не менш побудуємо обчислювальний алгоритм наближеного розв’язку даної задачі.

1.2 Сітки

Перша основна ідея чисельного розв’язання подібного роду задач полягає в тому, що розв’язок шукається не у всій смузі, а тільки в окремих її точках, на так званій сітці.

Побудуємо в смузі, у якій поставлена наша задача Коші, сітки. Нехай - крок по осі ; ( - натуральне ) - крок за часом ; ; - шуканий розв’язок в точках з координатами

Сіткою в даній задачі будемо називати кожну з наступних трьох множин точок (вузлів):

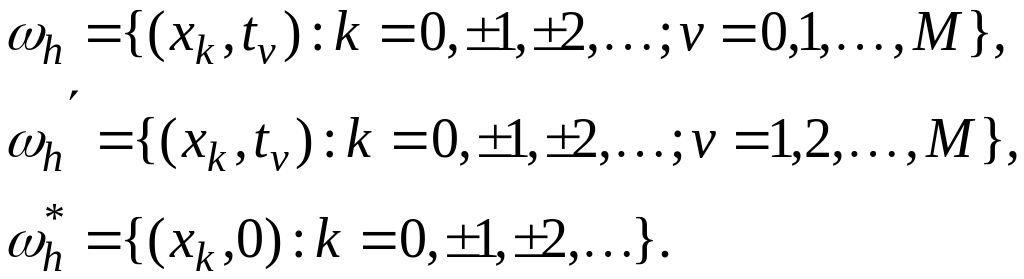
На рис.1 сітка відображена графічно:

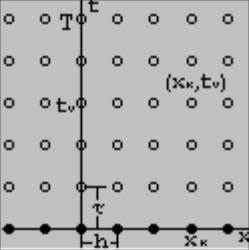
Рисунок 1

Сітка складається з вузлів, розташованих на осі абсцис, де задана початкова умова (2). Сітка є об'єднанням сіток і .

Функція , областю визначення якої є яка-небудь сітка або , називається сітковою. Значення сіткової функції у вузлах будемо для стислості позначати

Для сіткових функцій, заданих на сітках і введемо відповідно норми

(5)

а відповідні нормовані простори будемо позначати

1.3 Різницева схема

Для розв’язку , взятого у вузлах сітки, очевидно, мають місце співвідношення

(6)

(7)

де пробігає всі цілочислові значення (додатні і від’ємні, а також 0), а .

Друга основна ідея сіткових методів розв’язання диференційних рівнянь є заміна похідних шуканої функції у вузлах сітки різницевими похідними по тих чи інших формулах чисельного диференціювання. У результаті виходить система лінійних алгебраїчних рівнянь, розв’язуючи яку одержують наближений розв’язок вихідної задачі у вузлах сітки.

Замінивши в рівнянні (6) частинні похідні і різницевими похідними і перепозначивши на , приходимо до різницевої схеми (до різницевої задачі Коші)

(8)

(9)

де

Ми перепозначили на тому, що не задовольняє в загальному випадку (8), а задовольняє деяка сіткова функція , можливо й близька в деякому сенсі до функції , але, загалом кажучи, відмінна від неї. і позначають різницеві оператори і , дія яких на сіткові функції у вузлах сітки визначається співвідношеннями (8),(9). Хоча різницева схема залежить від двох параметрів і , для позначення різницевих операторів, сіток і норм заради простоти використовується тільки один індекс  .

Різницева схема (8),(9) коротко може бути записана у вигляді

на , на . (10)

У різницеве рівняння (8) при фіксованих і входять три невідомі і , що відносяться відповідно до вузлів і . Точки (вузли), у яких використовуються значення функції в різницевому рівнянні при фіксованих , називають шаблоном різницевого рівняння.

Шаблон розглянутого різницевого рівняння має вигляд: