2.2 Ітераційні методи розв’язання алгебраїчних і трансцендентних рівнянь

Розглянемо застосування принципу стискаючих відображень до дослідження збіжності ітераційного методу розв’язання рівнянь.

Припустимо, що рівняння (2.19) має корінь і в колі функція задовольняє умові Ліпшіца⁹:

(2.20)

для будь-яких точок .

Теорема 2.3 Для будь-якого послідовність

(2.21)

збігається до , якщо лише в колі задовольняє умові Ліпшіца з константою , при цьому швидкість збіжності характеризується нерівністю

. (2.22)

Доведення Сукупність точок кола , якщо визначити відстань між точками і відношенням , утворює повний метричний простір. Якщо , то також належить , оскільки

Таким чином, відображення, що визначається функцією , є відображенням повного метричного простору в себе. Воно є стискаючим відображенням, оскільки для будь-яких

і .

Тому за принципом стискаючих відображень в існує одна і лише одна нерухома точка, і ця точка є . Цю точку можна отримати як границю послідовності

при будь-якому .

Використовуючи умову Ліпшіца (2.20), маємо:

_.

Таким чином збігається до зі швидкістю геометричної прогресії зі знаменником . 

В доведеній теоремі припускалось існування кореня рівняння (2.19). Принцип стискаючих відображень може бути застосований і для доведення існування кореня.

Теорема 2.4 Якщо функція в деякому колі задовольняє умові Ліпшіца (2.20) з константою і в точці має місце нерівність

, (2.23)

то в рівняння (2.19) має єдиний корінь , який може бути знайдений як границя послідовності

,

де - будь-яка точка з кола .

Доведення слідує безпосередньо з теореми 1.3 (впевнитись самостійно).

Виникає питання, коли виконується умова Ліпшіца (2.20) з константою . Зокрема, це буде тоді, коли в деякому колі з центром в точці функція має безперервну похідну , яка по модулю не перевищує деякого числа , меншого одиниці, тобто

.

Це слідує з формули Лагранжа¹⁰ скінченого приросту

.

В цьому випадку розглянемо геометричну інтерпретацію процедури (2.21), припускаючи, що - дійсна функція змінного і - дійсний корінь рівняння (2.19). На рисунках зображені послідовні ітерації для випадків, коли і . В останньому випадку по двом послідовним наближенням до кореня можна судити про досягнуту точність на кожному кроці, оскільки відхилення від не більше

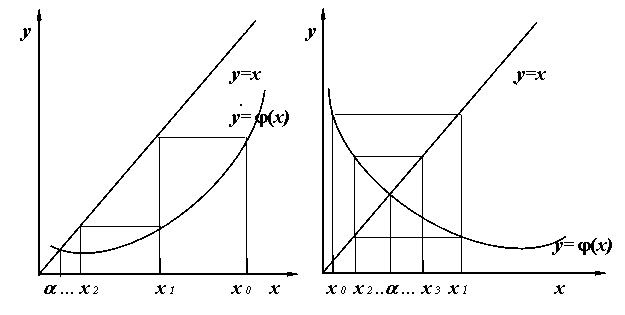
Рисунок 2.1

Зазвичай, вихідне рівняння задається у вигляді

. (2.24)

Потім це рівняння заміняється еквівалентним йому у вигляді (2.19) з метою застосування ітераційного методу розв’язання. В найпростіших випадках функція вибирається у вигляді

, (2.25)

де - деяка неперервна знакопостійна функція. Таким чином рівняння (2.24) зводиться до вигляду

, (2.26)

що відповідає представленню (2.19). Функція підбирається такою, щоб (2.25) було стискаючим відображенням в деякому околі кореня .

Розглянемо найпростіші способи вибору функції в (2.26), що відповідає найпростішим методам розв’язання рівняння (2.24): методу хорд (січних) і методу дотичних (Ньютона¹¹).