ЗМІСТ

1.1 Метричні простори 4

1.2 Принцип стискаючих відображень 10

1.3 Лінійні нормовані простори 16

2 УМОВИ ЗБІЖНОСТІ ІТЕРАЦІЙНИХ МЕТОДІВ РОЗВ’ЯЗАННЯ РІВНЯНЬ І СИСТЕМ 27

2.1 Системи лінійних алгебраїчних рівнянь 27

2.2 Ітераційні методи розв’язання алгебраїчних і трансцендентних рівнянь 36

2.2.1 Метод хорд 40

2.2.2 Метод дотичних (Ньютона) 43

3.1 Багаточлени Чебишова 46

3.2 Властивості багаточленів Чебишова 48

3.3 Вузли, які мінімізують оцінку похибки інтерполяції 49

4.1 Межі розташування коренів алгебраїчного рівняння 51

4.2 Число дійсних коренів алгебраїчного рівняння на відрізку 54

4.3 Відділення дійсних коренів алгебраїчного рівняння 60

ЛІТЕРАТУРА 64

1 Деякі відомості із функціонального аналізу

1.1 Метричні простори

Означення 1 Метричним простором називається пара ( , ), яка складається з деякої множини (простору) елементів (точок) і відстані (метрики) , тобто однозначної, невід’ємної, дійсної функції ( ), визначеної для будь-яких і з та які задовольняють наступним трьом вимогам:

1) ( ) = 0 тоді і лише тоді, коли = ;

2) (аксіома симетрії): ( ) = ( );

3) (аксіома трикутника): ( ) ≤ ( ) + ( ).

Метричний простір, тобто пару ( , ), зазвичай позначають однією літерою: = ( , ).

Розглянемо деякі приклади метричних просторів.

а) Множина дійсних чисел з відстанню ( ) = |x – y| створює метричний простір .

Те, що 1) і 2) аксіоми виконуються очевидно. Аксіома 3) є відомою нерівністю трикутника для дійсних чисел

|x – z| = |x – y + y – z| ≤ |x – y| + |y – z|

б) Множина впорядкованих груп із дійсних чисел (множина векторів)

= ( ₁, ₂,..., _n)

з відстанню між його елементами, яка визначається за формулою

.

Вірність аксіом 1) – 3) очевидна. Цей простір позначимо .

в) Множина впорядкованих груп з дійсних чисел = ( ₁, ₂,..., _n) з відстанню, яка визначається за формулою

.

Вірність аксіом 1) – 3) очевидна. Позначимо цей метричний простір R₁ⁿ.

г) Множина впорядкованих груп із дійсних чисел = ( ₁, ₂,..., _n) з відстанню, яка визначається за формулою

називається -вимірним арифметичним евклідовим простором .

Вірність аксіом 1) і 2) для очевидна. Покажемо, що в виконується і аксіома трикутника 3).

Для цього скористаємось нерівністю Коші-Буняковського¹,

, (1.1)

яка виходить з тотожності

.

Нехай = ( ₁, ₂,..., _n), = ( ₁, ₂,..., _n), = ( ₁, ₂,..., _n). Тоді аксіома трикутника приймає наступний вигляд

, (1.2)

Припускаючи і , отримуємо , а нерівність (1.2) при цьому приймає вигляд

. (1.3)

Але ця нерівність одразу виходить із нерівності Коші-Буняковського (1.1), оскільки

.

Тим самим нерівність (1.3), а звідси і нерівність (1.2) доведені.

д) Множина всіх неперервних дійсних функцій, визначених на сегменті , з відстанню

,

також утворює метричний простір. Аксіоми 1) – 3) перевіряються безпосередньо.

е) Розглянемо, як і в попередньому прикладі, сукупність всіх функцій, неперервних на відрізку , але відстань визначимо іншим шляхом

.

Такий метричний простір називається простором неперервних функцій з квадратичною метрикою і позначається .

Тут аксіоми 1) і 2) метричного простору очевидні, а аксіома трикутника безпосередньо виходить з інтегральної форми нерівності Коші-Буняковського²

,

яку можна отримати із тотожності, яку легко перевірити

.

Довести самостійно вірність аксіоми 3).

Нехай ₁, ₂,... – послідовність точок в метричному просторі .

Означення 2 Говорять, що послідовність { } збігається до , якщо виконується умова:

,

точка називається границею послідовності { }.

Означення 3 Послідовність { } точок метричного простору називається фундаментальною, якщо вона задовольняє критерій Коші, тобто якщо для будь-якого > 0 існує таке число N , що ( , )< для всіх > N , > N .

Із аксіоми трикутника безпосередньо виходить, що будь-яка послідовність, що збігається, є фундаментальною. Дійсно, якщо { } збігається до , то для данного >0 можна знайти таке число N _, що ( , )< для кожного > N .

Тоді ( , ) ( , ) + ( , )< для будь-яких > N , > N .

Обернене твердження, в загальному випадку, не вірне. Тобто не в кожному метричному просторі фундаментальні послідовності збігаються до точок із . Тривіальним прикладом може бути множина раціональних чисел з відстанню типу а).

Означення 4 Якщо у метричному просторі будь-яка фундаментальна послідовність збігається, то цей простір називається повним.

Розглянемо приклади повних метричних просторів:

а') Повнота простору – сукупності дійсних чисел відома з класичного аналізу. В критерій Коші являється критерієм збіжності послідовності { }.

б') Повнота простору безпосередньо випливає із повноти . Справді, нехай { ^(p)} – фундаментальна послідовність точок із ; це означає, що для кожного >0 знайдеться таке N = N , що

для всіх p,q > N. Тут ^(p)=( ₁^(p),..., ^(p)), ^(q)=( ₁^(q),..., ^(q)). Тоді для кожного отримуємо відповідну нерівність для координати _k^(p):

для всіх p,q > N. Таким чином { _k^(p)} – фундаментальна послідовність в , а тому вона збіжна.

Припустимо і ,

Тоді, очевидно,

.

в')-г') Повнота просторів і доводиться аналогічно (довести самостійно).

д') Доведемо повноту простору .

Нехай { (t)} – деяка фундаментальна послідовність в . Це означає, що для кожного >0 існує таке N = N , що

при n, m > N для всіх t, a t b. Звідси виходить, що послідовність { (t)} рівномірно збігається. Із класичного аналізу відомо, що у цьому випадку її границя (t) буде неперервною функцією. Спрямувавши в попередній нерівності m до нескінченності, отримаємо

для всіх t [a,b] і для всіх n > N, а це і означає, що { (t)} збігається до (t) в метриці простору .

е') Простір неповний. Розглянемо, наприклад, послідовність неперервних функцій

=

Вона фундаментальна в [-1,-1], оскільки, враховуючи парність підінтегральної функції (рис. 1.1),

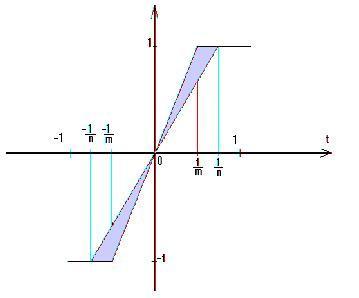
Рисунок 1.1

.

Однак вона не збігається до жодної функції із [-1,-1]. Дійсно, нехай f – деяка функція із [-1,-1] і - функція з розривом, яка приймає значення -1 при t < 0 i +1 при t ≥ 0.

Із нерівності Коші-Буняковського (справедливого і для кусково-неперервних функцій) виходить, що

.

В силу неперервності функції f інтеграл у лівій частині відмінний від нуля. Далі, зрозуміло, що

.

Тому не може прямувати до нуля при n .