7. Метод математической индукции

При использовании метода МИ выдел.4 этапа:

1, Создание базы индукции – здесь проверяется истинное р(n) при n=1.

2,Допущение индукции – здесь формулируем, что p(n)- и .

3, Шаг индукции – здесь доказывается истинность от p(n+1) при использовании истинности р(n).

4,Вывод – здесь делается заключение об истинности р(n) при любом n.

1-проверим

2-допустим

3-докажем

4-вывод: согласно принципу МИ (условие) при любом натур. n

Чтобы избежать вынужденной адаптации формулировок, можно соотв.образом адаптировать сам признак.

Для доказательства того, что определенное утверждение р(n) о натур.числех истинно при всех n начиная с n0 можно использовать такой вариант принципа МИ ( с модимиц. Базой индукции) Если утверждение о натур.числах n – истинно при n-n0 – и, из того, что р(n) – n при n=k n следует истинность р(n) при n=k+1, то р(n) – и при всех n n0.

Иногда полезно применить формулировку принц. МИ с модиф.допущ:

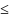Если утверждение р(n) о натур.числах при n 1 –и , из того, что р(n) истинно при всех n k следует истинность р(n) при n=k+1, то р(n) истинно при всех натур. n.

Будем проводить индукцию по количеству операций:

1, База индукции: при n 1 очевидно

2, Допустим, что при использовании не более чем k операций возможно тождественная замена выражения на не более чем с одним использованием операций делания.

3, Пусть имеем высказывание с k+ одной операцией, обратим внимание на последнюю операцию, она выполняется над частичными выражениями, каждая из которых содержит не более чем k операций. Значит по допущению МИ каждая из частичных выражений сводится к выражению с неболее, чем 1 применением деления. Значит исходное выражение сводится к сумме, разности, произведению или частному 2 целых выражений или или дробей, а может быть заменения одной дробью или целым(без деления) выражением.

4, В соответствии с принципом МИ утверждение, указанное в условии,утвер.истинно для любого количества операций.

8. Множество. Отношения между множествами, их свойства.

Множество = совокупность .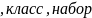

Множество и элементы мн. Находятся в отношении: множество состоит из элементов.

Множества: А,В,С. Элементы: а, b,с.

То, что а принадлежит М, обознач: a€М.

Сущ.пустое множество – ø.

Задание множеств.

1.Перечисление всех элементов множества( перечисляются все элементы и заключ в {}). Годится для конечных мн. с небольших числом э.

2. Указание характерисистического св-ва – наз высказывательную форму обычнос 1ой переменной, которая и превращается в ист.высказывание только при подстановке вместо переменной элементов данного мн-ва.

3.Множество названное специально(натур, целых, действ чисел)

Говорят: М а вкюч.во множество М в, если каждый элемент М а принадлежит М в.(или М а есть подмножество в)

! М называется равным , если они состоят из одних и тех же элементов. Это одно и то же М, только заданное разными списобами.

Св-ва отношения включ.мн.

1,рефлексивно (любое мн включает само себя)

А, А€А

2,антисимметрично

3,транзетивно

Св-ва отношения равенства мн.

1,рефлексивно

2,симметрично

3,транзетивно

9. Операции над множествами, их свойства.

1,Пересечением 2 мн. А и В наз мн А и В только тех элементов, которые принадлежат и мн А, и мн В.(т.е. их общая часть)

2,объединением 2 мн А и В наз мн тех и только тез элементов, котрые принадлежат мн А или мн В

3,разностью 2 мн А и В наз мн тех и только тех элементов А, котрые не принадлежат В.

10. Декартово пр.множеств.Бинарное отношение.Св.бин.отнош.

*Под парой будем понимать упорядоченное мн из 2 элементов (а, в). Пары будем считать равными, если равны их соотв. Элементы.

*Декартовым(прямым) произв. 2 мн а и в называют мн всевозможных пар, первый элемент которых принадлежит мн а, а 2 – мн в.(обознач ( АхВ) )

*Декартовым произведением мн А1, А2,….Аn наз мн всевозможных пар n элементов, первый элемент которых принадлежит А1, 2ой – А2 и т.д.

*Бинарным отношением между элементами множеств А и В наз подмножество р(ро) их декартово произвед АхВ

Если р=А*В, то бинарное отношение наз. УНИВЕРСАЛЬНЫМ, если р=ø, то наз ПУСТЫМ

Св. бинарных отнош:

1,рефлексивности

(Н-р: равенства чисел, паралл.прямых на плоскости)

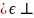
2,антирефлексивности

3,симметричности

4,антисимметричности

5,ассиметричности

6,тринзетивности

7.антитранзетивности

8,связности бин.отнош

ГРАФ-множество точек вершин графа соединенных линиями ребрами графа. Граф это отношение стрелок от а к б

1)рефлексивность каждая точка графа имеет петлю

2)антирефлексивность ни одна точка не имеет петлю

3)симметричность все стрелки двухголовые

4)антисимметричность нет 2-х головых стрелок но есть петли

5)ассиметричность нет пятель нет 2-х головых стрелок

6)транзитивность есть стрелка от А к В от В к С и от А к С.

7)антитразитивность нет ни одного замкнутого треугольника

8)связность для любых 2-х точек от А к В либо от В к А либо это одна и таже точка

ГРАФИКОМ-бинарных отношений будет множество точек плоскости координаты которых числа связанные данным бинарным отношением.

1)рефлексивность отношения означает принадлежность к графику всех точек прямой у=х

2)антирефлексивность – означает что ни одной точки прямой у=х график не принадлежит

3) симметричность – симметричность графика относительно прямой у=х

4)антисимметричность – означает если есть точки симметричные относительно прямой у=х то это только точки этой прямой

5) ассиметричность симметричных точек вообще нет

6)транзитивность для всех прямоугольников стороны которых параллельны осям координат если одна вершина принадлежит прямой у=х две другие принадлежат графику то и 4-ая вершина пренадлежит графику.

7)антитразитивность нет таких прямоугольников .

8)связность для любой точки плоскости либо она сама принадлежит графику либо симметричная ей относительно прямой у=х принадлежит графику либо это точка прямой у=х

12. Функциональные отношения:

Бинарное отношение р(ро) между элем мн а и в наз функциональным или функцией с областью определения а и обл знач в, если оно удовлетворяет условию

*Отображение А во мн В наз инъекцией, если каждый элемент мн В явл образом не более 1элем из А.

*Биекция – это отображение, которое одновременно явл сюрьекцией и инъекцией

11.Отнош.эквивалентности.Классы эк, Фактор-множество.

*Теорема: Отношение р(ро), определенное на мн n, являясь отношением эквивалентности разбивает это мн на классы. Все элементы одного класса связаны между собой этим отношением. Элементы из разных классов не связваны; разные классы пересекаются по пустому мн. Объед всх классов – все мн n.

Классыих бесконечно много)

1,

Пучки паралл. прямых

2,

3,

4,

5,

Если отношение эквивалентности таково, тчо классы экв.содержат точно по 1элем – это отношение наз отнош.равенства

Теорема: Если мн разбито на непересекающ.классы, то в нем можно определить отношение эквивалентности

12. Функциональные отношения

13. Отношения порядка

*Рефлексивные, антисимметричные и транзитивные бинарные отношения наз отношением нестрогого частичного порядка

*Антирефлексивное, ассиметричное и транзетивное бинарное отнош - отнош строгого частичного парядка

* Отнош нестрогого частичного порядка, облад св-ом связности наз нестрогим линейным порядком (нестрогим порядком)

*Отнош строгого частичного пор наз отношением строгого линейного порядка(отн стр порядка), если это отношение связно

*Итак, Строгий порядок – это антирефлексивног ассиметричное транзитивное и связное бинарное отношение.

14.Комбинаторные задачи и правила

Задачи, в которых приходится выбирать из некоторого мн объектов его подмножества или размещать элементы некоторого мн в определенном порядке – наз комбинаторными.иногда используется схема «логических способностей»

15. Правило комбинаторного сложения

*Если множество А содержит m элементов, а в множестве В n элементов, и множества А и В не пересекаются, то их объединение ( А U В) содержит m+n элементов.

*Правила суммы позволяет найти количество элементов в объединении нескольких множеств, если эти множества парно не пересекаются.

Если выбор одного объекта можно произвести р1 –различными способами, выбор 2-ого объекта р2 -различными способами, которые отличаются о предыдущих и т.д. выбор n-ого объекта рn- способами, то выбор какого-нибудь объекта из всех данных объектов можно произвести р1+р2+р3+…+рn способами.