17. Простая и взвешенная средняя арифметическая.

Средняя арифметическая может быть простой и взвешенной. Средняя арифметическая простая равна сумме произведений значений признака, деленной на их количество.

, где – значение признака у i-ой единицы совокупности; – число единиц наблюдения в исследуемой совокупности.

Если одно и то же значение признака встречается несколько раз, то рассчитывается средняя арифметическая взвешенная по формуле:

,

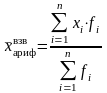где 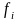– частота, т. е. число случаев возникновения i-го значения признака.

18. Основные свойства средней арифметической. 1. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю. 2. Если от каждой варианты вычесть или прибавить к ней произвольное число А, то средняя арифметическая соответственно уменьшиться или увеличится на это же число А. 3. Если каждую варианту разделить или умножить на какое-либо произвольное число h, то и средняя также соответственно уменьшится или увеличится в h раз. 4. Если все частоты разделить или умножить на какое-либо число А, то средняя арифметическая не изменится. Упрощенные способ расчет средней арифметической, используя ее математические свойства (способ моментов). ӿ=h*m+A, где m – условный момент первого порядка. В качестве А предпочтительно брать значение признака с наибольшей частотой, в качества h- шаг интервала. M1 = (Сумма ((Xi-A)/h)*Fi)/Сумма Fi.

19. Средняя гармоническая. Расчет средней гармонической простой и взвешенной.

При m=-1. Средняя гармоническая простая – средняя величина из обратных значений признака. Средняя гармоническая простая рассчитывается по следующей формуле: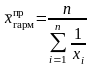

В тех случаях, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной: .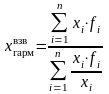

20. Виды степенных средних – средняя геометрическая, средняя квадратическая.

Средняя квадратическая применяется только тогда, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы.

Средняя квадратическая может быть простой и взвешенной и определяется соответственно по формулам: , .

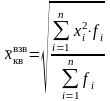Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел. Поэтому средняя геометрическая используется в расчетах среднегодовых темпов роста.

или ,

где где – относительная величина динамики цепная; – относительная величина динамики базисная.

21. Средние позиционные: мода и медиана

Структурные средние – позиционные – занимают определенное место (позицию) в вариационном ряду. Мода - значение признака, наиболее часто встречающееся в исследуемой совокупности. В дискретных вариационных рядах – мода, это значение варианты с наибольшей частотой. 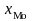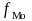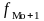В интервальных вар.рядах определяется модальных интервал – интервал с наибольшей частотой, мода определяется по формуле: где – нижняя граница модального интервала; – величина модального интервала; – частота модального интервала; – частота интервала, предшествующего модальному; – частота интервала, следующего за модальным. Модальный интервал определяется по наибольшей частоте.

Медиана – значение признака, приходящегося на середину ранжированной совокупности. В Ранжированном ряду с нечетным числом членом n- медианой является варианта, расположенная в центре ряда. Порядковый номер медианы: Nme=(n+1)/2. При четном числе членов n медиана определяется как средняя из двух центральных вариант. В дискретном вариационном ряду определяются накопленные частоты. Далее по данным о накопленных частотах находят медиану – значение признака, у которого накопленная частота составляет половину или впервые превышает половину суммы всех накопленных частот. Медиана интервального ряда определяется по формуле: ,

где 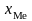– нижняя граница медианного интервала; – величина медианного интервала; 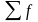– сумма частот ряда; – сумма накопленных частот интервала, предшествующего медианному; – частота медианного интервала.

22. Средние позиционные: квартиль и дециль

Квартиль – значение признака, делящее ранжированную совокупность на 4 равные части. Различают квартиль нижний, отделяющий ¼ часть совокупности (25%) с наименьшими значениями признака. Квартиль средний делит совокупность пополам (медиана). Квартиль верхний отделяет ¼ часть совокупности с наибольшими значениями признака. ;

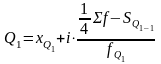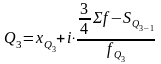
Децили – значения вариант, которые делят ранжированный ряд на 10 равных частей.