26 Статистическая гипотеза. Нулевая и конкурирующая гипотезы. Статистические критерии проверки нулевой гипотезы. Область принятия нулевой гипотезы.

Критическая область и ее отыскание. Мощность критерия.

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Например, статистическими будут гипотезы:

1. генеральная совокупность распределена по закону Пуассона;

2. дисперсии двух нормальных совокупностей равны между собой.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.

Нулевой (основной) называют выдвинутую гипотезу .

Конкурирующей (альтернативной) называют гипотезу которая противоречит нулевой.

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину обозначают через U или Z, если она распределена нормально, F или — по закону Фишера — Снедекора, Т — по закону Стьюдента, — по закону «хи квадрат» и т. д. Поскольку в этом параграфе вид распределения во внимание приниматься не будет, обозначим эту величину, в целях общности, через К.

Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки нулевой гипотезы.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин, и таким образом получают частное (наблюдаемое) значение критерия.

Критической областью называют область значений критерия, при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают.

Область принятия нулевой гипотезы (область допустимых значений) – совокупность значений критерия, при котором нулевую гипотезу принимают. При справедливости нулевой гипотезы вероятность того, что статистика критерия попадает в область принятия нулевой гипотезы должна быть равна 1-Ркр.

Порядок проверки статистической гипотезы таков:

1) задается уровень значимости α, выбирается статистический критерий К и вычисляется (обычно по таблицам для закона распределения К) значение kкр; определяется вид критической области;

2) по выборке вычисляется наблюдаемое значение критерия Кнабл;

3) если Кнабл попадает в критическую область, нулевая гипотеза отвергается; при попадании Кнабл в область принятия гипотезы нулевая гипотеза принимается.

Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что верна конкурирующая гипотеза.

Если обозначить вероятность ошибки второго рода (принятия неправильной нулевой гипотезы) β, то мощность критерия равна 1 – β. Следовательно, чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода. Поэтому после выбора уровня значимости следует строить критическую область так, чтобы мощность критерия была максимальной.

27 Критерий Пирсона проверки статистических гипотез

для проверки нулевой гипотезы Н0: генеральная совокупность распределена нормально – нужно вычислить по выборке наблюдаемое значение критерия:

а по таблице критических точек распределения χ2 найти критическую точку , используя известные значения α и k = s – 3. Если - нулевую гипотезу принимают, при ее отвергают.

ПЕРЕСТРОЕНИЯ. P_n=n!

A_n^m=n!/(n-m)! без повторений. Ӑ_n^m=n^m с повторениями

СОЧЕТАНИЯ (порядок не важен) C_n^m=n!/m!(n-m)!

Р(А+В)=Р(А)+Р(В) несовм Р(АВ)=Р(А) Р_А(В) завис

Р(А+В)=Р(А)+Р(В)–P(AB) совм Р(АВ)=Р(А) Р(В)независ

Р(А)=Р(Н1) Р_Н1(А) +…+ Р(Нn) Р_Нn(А)

Р_А (Нi)= Р(Нi) *Р_Нi(А) / Р(А) байес

Бернулли: p_n(k)=C_n^k * p^k * q^n-k

np-q≤m≤np+p наивероятн

локальн формула Лапласа

интегральной формуле Лапласа

формула Пуассона

М(Х)=m_x=∑x_ip_i

М(Х)=m_x=∫_–∞^+∞ xf(x)dx

Для непрерывной СВ Х D(X)= ∫_–∞^+∞(x–m_x)²f(x)dx

Для дискретной СВ Х D(X)= ∑(x_i–m_x)²p_i

σ_х=√D(X)

Биномиальный Pn(X=m)= C_n^m * p^m * q^n-m . В этом случае mx=np , D(X)=npq

Пуассона М(X)=D(X)=λ

. нормальный M(X)=a, D(X)= σ²

Показательное M(X)=1/ λ D(X)=1/ λ² σ(X)= 1/ λ

Равномерное С = 1/(b – a)

1.) ПЕРЕСТРОЕНИЯ. P_n=n!

A_n^m=n!/(n-m)! без повторений. Ӑ_n^m=n^m с повторениями

C_n^m=n!/m!(n-m)! СОЧЕТАНИЯ (порядок не важен)

2.) Р(А+В)=Р(А)+Р(В) несовм Р(АВ)=Р(А) Р_А(В) завис

Р(А+В)=Р(А)+Р(В)–P(AB) совм Р(АВ)=Р(А) Р(В)независ

р(неН1*H2+H1*неН2) Не более 4 : 1-(р5(6) + р6(6))=1-С6⁵*Н1⁵*неН1¹- С6⁶*Н1⁶*неН1⁰

3) Р(А)=Р(Н1) Р_Н1(А) +…+ Р(Нn) Р_Нn(А)

Р_А (Нi)= Р(Нi) *Р_Нi(А) / Р(А) байес

4) ХАР-КИ ДСВ : F(X)= (от 0 до 1) Если надо, по накоплению идет

М(Х)=m_x=∑x_ip_i

D(X)=M(X²)- (M(X))² = ∑(x_i–m_x)²p_i

σ_х=√D(X)

5)нормальный

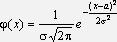M(X)=a, D(X)= σ²

Р(α<X<β)= Ф(β - a )/σ – Ф(α - a )/σ

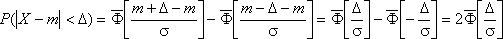
6) f(x)= F’(x)= производная

М(Х)=m_x=∫_–∞^+∞ xf(x)dx

D(X)= ∫_–∞^+∞x²f(x)dx – (М(Х)) ²

σ_х=√D(X)

P(a<x<b)=F(b)–F(a)

7) закон распр ДСВ

р(х=0)=р(неН1*неН2) р(х=0)=С₈⁰*С₂²/С₁₀²

р(х=1)=р(неН1*Н2+Н1*неН2) р(х=1)= С₈¹*С₂¹/С₁₀²

р(х=2)=р(Н1*Н2) р(х=2)= С₈²*С₂⁰/С₁₀²

М(Х)=m_x=∑x_ip_i

D(X)=M(X²)- (M(X))² = ∑(x_i–m_x)²p_i

σ_х=√D(X)

8) НЕСМЕЩ ОЦЕНКИ

ẍ_в=∑x_in_i/∑n_i несмещ оценка ген.средней

D_в= ∑x_i²n_i/∑n_i – ẍ_в² = 1/n∑(x_i– ẍ_в) ² n_i

S²= n/(n–1)* D_в несмещ оценка дисперсии

13