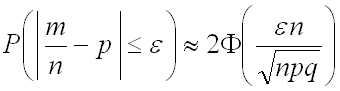5. Теоремы о вероятности произведения независимых и зависимых событий
Два события А и В называются независимыми, если вероятность появления каждого их них не зависит от того, появилось другое событие или нет. В противном случае эти события называют зависимыми.
Пусть А и В – зависимые события. Условной вероятностью РА(В) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило: Р(АВ)=Р(А) РА(В)
Док-во: пусть из всего числа n элементарных событий k благоприятствуют событию А, и пусть из этих k событий l благоприятствуют событию В, а значит, и событию АВ. Тогда Р(АВ)=l/n=k/n * l/k=Р(А) РА(В)
Если события А и В независимы, тогда Р(АВ)=Р(А) Р(В)
6. Формула полной вероятности. Формула Байеса
Пусть событие А может произойти лишь при условии появления одного из n попарно несовместимых событий Н1, Н2…Нn, образующих полную группу событий. События Н1, Н2…Нn называются гипотезами для события А. Тогда Р(А)=Р(Н1) РН1(А) +…+ Р(Нn) РНn(А)
Это формула полной вероятности.
Из формулы полной вероятности следует формула Байеса, позволяющая произвести переоценку вероятностей гипотез после того, когда событие А произошло:
РА (Нi)= Р(Нi) *РНi(А) / Р(А)
Док-во: по теореме умножения вероятностей и формуле полной вероятности имеем: Р(АНi)=Р(А) РА(Hi)= Р(Hi) РHi(A). Отсюда: РА(Hi)= Р(Hi) РHi(A) / Р(А). Используя формулу полной вероятности, находим: РА(Hi)= Р(Hi) РHi(A) / ∑Р(Нk) РНk(А)
7. Формула Бернулли. Наивероятнейшее число появления события в серии испытаний
Пусть вероятность события А одинакова во всех n независимых испытаниях и равна p(A)=p. Тогда p(Ā)=1-p=q. Тогда вероятность того, что в n испытаниях событие А появится ровно k раз, вычисляется по формуле Бернулли: pn(k)=Cnk * pk * qn-k
Число появления события А, вероятность которого наибольшая, называется наивероятнейшим числом. Обозначим наивероятнейшее число наступления некоторого события А в серии из n испытаний через m.
Pn(m)≥ Pn(m-1) (1) Pn(m)≥ Pn(m+1) (2)
Распишем неравенство (1) использую формулу Бернулли.
Pn(m) / Pn(m-1) ≥1
Cnm * pm * qn–m / Cnm–1 * pm-1 * qn–m+1 ≥1
n!(n-1)!(n-m+1)!p / m!(n-m)!n!q ≥1
(n-m+1) / m * p/q ≥1
(n-m+1)p≥qm
(n+1)p ≥qm+pm (n+1)p ≥(q+p)m m≤np+p
Поступая аналогично с неравенством(2),получим m≥np-q. np-q≤m≤np+p
8. Формула Пуассона. Локальная и интегральная формулы Лапласа. Вероятность отклонения относительной частоты события от его вер-ти
Если n – велико, p – среднее значение, то для вычисления вероятности наступления события А k раз в серии из n независимых испытаний находится по локальной формуле Лапласа
Для расчета вероятности того, что событие А в серии из n независимых испытаний появится от k1 до k2 раз, находится по интегральной формуле Лапласа
Если n велико, а вероятность наступления события мала, то для нахождения вероятности k раз в n независимых испытаниях используется формула Пуассона
Отношение числа испытаний, в которых событие А появилось, к общему числу фактически проведенных испытаний называется относительной частотой события. w(A)=m/n. Разница между относительной частотой события и его вероятностью в том, что вероятность рассчитывается до опыта, а относительная частота – после.
Вероятность того, что отклонение относительной частоты от вероятности события по модулю не превышает заданного значения Ɛ, находится по формуле
