20. Точечные оценки неизвестных параметров распределения, их классификация. Точечные оценки генеральной средней и генеральной дисперсии. Доказательство смещенности выборочной дисперсии
Оценка
параметра
— определенная числовая характеристика,
полученная из выборки. Точечной
называют статистическую оценку, которая
определяется одним числом. В качестве
точечных оценок параметров генеральной
совокупности используются соответствующие
выборочные характеристики. Несмещенной
называют точечную оценку, математическое
ожидание которой равно оцениваемому
параметру при любом объеме выборки.
Смещенной
называют точечную оценку, математическое
ожидание которой не равно оцениваемому
параметру. Выборочная
средняя
является точечной оценкой генеральной
средней, т. е. Несмещенной
оценкой
генеральной средней (математического
ожидания)служит выборочная средняя.
Генеральная дисперсия имеет две точечные
оценки: — выборочная дисперсия, которая
исчисляется при н
30;
S^2 — исправленная выборочная дисперсия,
которая исчисляется при n < 30. Причем
в математической статистике доказывается,
что
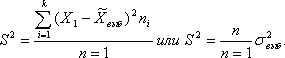
21 Доверительный интервал для оценки мат ожидания нормально распределенной св при известном среднем квадратическом отклонении
Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр.
Для
оценки математического ожидания
случайной величины , распределенной по
нормальному закону, при известном
среднем квадратическом отклонении
служит доверительный интервал
где
- точность оценки,
- объем выборки,
- выборочное среднее,
- аргумент функции Лапласа, при котором
22 Доверительный интервал для оценки мат ожидания нормально распределенной св при неизвестном среднем квадратическом отклонении
Для
оценки математического ожидания а
(генеральной средней) нормально
распределенного количественного
признака Xпо выборочной средней при
неизвестном среднем квадратическом
отклонении
генеральной
совокупности (на практике — при малом
объеме выборки, т. е. при п < 30) и
собственно-случайном повторном отборе
формула (6.6) будет иметь вид
(6.8) где t определяется по таблицам
Стьюдента, по уровню значимости
и
числу степеней свободы k = n
- 1; — исправленное выборочное среднее
квадратическое отклонение; n
— объем выборки.
23 Доверительный интервал для оценки среднего квадратического отклонения нормально распределенной св.
Доверительные интервалы для оценки среднего квадратического отклонения а нормального распределения количественного признака Z генеральной совокупности
С надежностью у по исправленному выборочному среднему квадратическому отклонению S определяются неравенствами S(1-q)<σ <S(1+q) при q<1;
0< σ <S(l+q) при q>l, где значения q находятся по таблице по заданным n и у.
24 Эмпирические и выравнивающие частоты. Нахождение выравнивающих частот для нормально распределенной св.
Дискретное распределение
Пусть изучается некоторая дискретная СВ Х,закон распределения которой неизвестен. Произведено n испытаний, в которых СВ Х n1 раз принимала значение х1 и т.д., nm раз принимала значение xm. Частоты ni получаемые в результате выборки называются эмпирическими. Для того чтобы проверить, по какому закону распределена СВ Х, вычисляют частоты наблюдаемых значений. Теоретическими (выравнивающими) частотами ni’ называются частоты, вычисленные по формуле: ni’=nPi , где Pi – вероятность принять значение xi, если СВ распределена по предполагаемому закону.
Непрерывное распределение
Весь интервал возможных значений делят на k непересекающихся промежутков и находят вероятности Рi попадания СВ в i-тый интервал. Для нормального закона используют формулу : Р(α≤х≤β)=Ф((β-ẍв)/σв) - Ф((α- ẍв)/σв). При построении теоретической кривой нормального распределения для нахождения выравнивающих частот используют формулу: ni’=nh/ σв, где h-длина частичного интервала