6.Однородное уравнение первого порядка

Функция 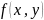- однородная функция п-го порядка относительно переменных х и у, если при любой ƛ справедливо тождество:

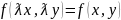
Уравнение первого порядка:

- называется однородным относительно х,у если функция f(x,y) является однородной функцией неравного измерения относительно х и у

Решение однородного уравенения:

По условию

Теперь возьмем . Получается

Уравнение в этом случае примет вид:

Сделаем подстановку:

y=Ux, тогда

Подставив в (2) получим:

=f(1,U)

Интегрируя находим:

Подставляя вместо U его значение получим интеграл уравнения

7.Линейные однородные ду. Решение уравнения

Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .

Например, функция есть однородная функция второго измерения, так как

При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как

Дифференциальное уравнение вида называется однородным относительно х и у , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде (1)

Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:

Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).

Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .

8.Уравнение Бернулли

Здесь Р(х) и Q(x) непрерывная функция от х, а п≠0≠ 1

Это уравнение можно привести к линейному сдел преоброзованием разделив его на

Делаем замену: z=

Получим

Подставим данное уравнение в 1е и получим:

Получили линейное уравнение

9.Уравнение в полных дифференциалах

Если дифференциальное уравнение имеет вид dy/dx = M(x,y)/N(x,y), где M и N – две заданные функции, то его можно представить как M(x,y)dx – N(x,y)dy = 0. Если левая часть является дифференциалом некоторой функции F(x,y), то дифференциальное уравнение можно записать в виде dF(x,y) = 0, что эквивалентно уравнению F(x,y) = const. Таким образом, кривые-решения уравнения – это «линии постоянных уровней» функции, или геометрические места точек, удовлетворяющих уравнениям F(x,y) = c. Уравнение ydy = xdx (рис. 1) – с разделяющимися переменными, и оно же – в полных дифференциалах: чтобы убедиться в последнем, запишем его в виде ydy – xdx = 0, т.е. d(y2 – x2) = 0. Функция F(x,y) в этом случае равна (1/2)(y2 – x2); некоторые из ее линий постоянного уровня представлены на рис. 1.

10. Особые решения ду 1 порядка

Особые точки и особые решения уравнения первого порядка. Если в окрестности точки (x₀, y₀) плоскости для уравнения выполняются условия существования и единственности решения задачи Коши (непрерывность f(x, y) и ), то через эту точку проходит единственная интегральная кривая. Если эти условия нарушаются, точку (x₀, y₀) называют особой точкой дифференциального уравнения. Через особую точку может не проходить ни одной и нтегральной кривой (т.е. задача , y(x₀) = y₀ не имеет решения); может проходить одна интегральная кривая; может проходить несколько интегральных кривых. Особые точки могут образовать кривую, которая сама является интегральной кривой уравнения. Решение уравнения, в каждой точке которого нарушается его единственность, называют особым решением. Для примера рассмотрим уравнение . Здесь - непрерывна в любой точке (x, y), но - не имеет конечного предела при , т.е. в любой точке (x, y) при y = 0 нарушается условие существования непрерывной производной . Следовательно, любая точка (x, 0) является особой точкой уравнения. Прямая y = 0, очевидно, интегральная кривая уравнения (функция y = 0 удовлетворяет уравнению). Найдём общее решение этого уравнения: . Несколько таких функций приведено на рисунке справа вверху вместе с решением y = 0. В любой точке (x, 0) нарушается единственность решения, таким образом, решение y = 0 - особое. На самом деле через любую точку (x, 0)проходит бесконечное количество интегральных кривых, так как любая кривая, составленная из частей особого и неособых решений (одна такая кривая выделена красным пунктиром), также является интегральной кривой.