33. Признак сравнения. Признак коши

Радикальный признак Коши — признак сходимости числового ряда:

Если для числового ряда

с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.

Предельная форма

Условие радикального признака равносильно следующему:

То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:

Если для ряда

, то

если   ряд сходится,

если l > 1 ряд расходится,

если l = 1 вопрос о сходимости ряда остается открытым.

34. Интегральные сходимости знакопостоянных рядов

Интегральный признак Коши

Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд

 сходится, если сходится несобственный интеграл  , и расходится, если  .

Формулировка теоремы

Пусть для функции f(x) выполняется:  (функция принимает неотрицательные значения)  (функция монотонно убывает)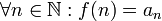  (соответствие функции ряду) Тогда ряд   и несобственный интеграл   сходятся или расходятся одновременно.

35. Знакочередующиеся ряды. Теорема Лейбница

 Знакочередующиеся ряды

     Переходя к рассмотрению рядов, члены которых уже не обязательно положительны, остановимся сначала на одном важном частном типе этих рядов - на рядах знакочередующихся, теория которых сравнительно проста.

     Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков.

     Несколько изменяя употреблявшуюся выше символику, будем обозначать через a_n не сам общий член ряда, а его абсолютную величину. Тогда, предполагая для определенности, что первый член знакочередующегося ряда положителен, мы сможем записать этот ряд в форме^*

a₁ - a₂ + a₃ - a₄ + a₅ - ...     (36)

     Теорема Лейбница. Если абсолютная величина общего члена знакочередующегося ряда убывает и стремится к нулю, то этот ряд сходится.

     Действительно, допустим, что ряд (36) таков, что

a₁ > a₂ > a₃ > a₄ > ...,     (37)

     (38)

Образуем частичные суммы S_2n:

                              S₂ = (a₁ - a₂),

                              S₄ = (a₁ - a₂) + (a₃ - a₄),

                              S₆ = (a₁ - a₂) + (a₃ - a₄) + (a₅ - a₆),

                              .   .   .   .   .   .   .   .   .   .   .   .   .   .

Благодаря (37), все скобки положительны. Значит,

S₂ < S₄ < S₆ < ...

     Иначе говоря, последовательность {S_2n} возрастает. С другой стороны,

S_2n = a₁ - (a₂ - a₃) - (a₄ - a₅) - ... - (a_2n-2 - a_2n-1) - a_2n,

откуда ясно, что

S_2n < a₁.

     Как известно, при этих условиях существует конечный предел

Но

S_2n+1 = S_2n + a_2n+1,

откуда в связи с (38) вытекает, что сумма S_2n+1 с возрастанием n также стремится к S. Итак, при достаточно больших n сумма S_n будет сколь угодно близка к Sнезависимо от четности n. Иначе говоря,

чем и доказана теорема.

     Заметим, что теорема перестает быть верной, если отбросить условие убывания a_n. Например, знакочередующийся ряд

как легко видеть, расходится