36. Знакопеременный ряд абсолютная и условная сходимость

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Абсолютная и условная сходимость знакопеременных рядов

Понятие знакопеременного ряда включает в себя как знакочередующиеся ряды, так и ряды с произвольным чередованием знаков своих членов. Знакопеременный ряд   сходится, если сходится ряд  . В этом случае знакопеременный ряд   называют абсолютно сходящимся. Сходящийся знакопеременный ряд   называют условно сходящимся, если ряд   расходится.

37 Функциональный ряд. Свойство равномерно сходящихся функциональных рядов

Определение 1.1. Функциональным рядом называется ряд вида

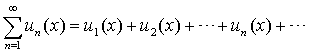    (1.1)

Определение 1.2. Множество значений переменной x, при которых ряд (1.1) сходится, называется областью сходимости

Свойства равномерно сходящихся рядов.

Теорема 2.1. Пусть все члены  функционального ряда (1.1) определены в некоторой области D, непрерывны в ней и составленный из них функциональный ряд сходится в этой области равномерно. Тогда суммой ряда (1.1) будет функция, непрерывная в области D.

Доказательство. Из непрерывности членов функционального ряда (1.1) следует непрерывность каждой из его частичных сумм (1.3). По условию эта последовательность частичных сумм сходится равномерно к предельной непрерывной функции S(x), являющейся суммой ряда (1.1). Теорема доказана.

 Теорема 2.2. (Почленное интегрирование ряда). Если функциональный ряд (1.1) сходится равномерно в некоторой области D и имеет сумму S(x), то функциональный (относительно переменной у) ряд интегралов

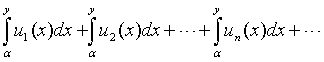   (2.1) (здесь  ) также сходится равномерно в этой области и имеет суммой функцию

   (2.2)

Доказательство. Пусть S_n(x) – n-я частичная сумма ряда (1.1). Тогда

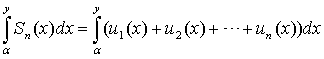   (2.3) будет, очевидно, n-ой частичной суммой ряда (2.1). По условию теоремы последовательность частичных сумм (1.3) ряда (1.1) сходится в области D равномерно. Следовательно, на основании теоремы о предельном переходе под знаком интеграла с переменным верхним пределом интегрирования последовательность интегралов

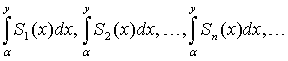   (2.4) также сходится равномерно и имеет пределом (2.2). Но в силу (2.3) интегралы (2.4) являются частичными суммами ряда (2.1). Тем самым доказаны равномерная сходимость ряда (2.1) и равенство его суммы интегралу (2.2). Теорема доказана.

38. Мажорируемый ряд.

39. Степенной ряд. Теорема Абеля

Теорема.  Если степенной ряд   сходится при x = x1 , то он сходится и притом абсолютно для всех  .

 

  Доказательство. По условию теоремы, так как члены ряда ограничены, то

где k- некоторое постоянное число. Справедливо следующее неравенство:

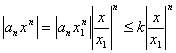
Из этого неравенства видно, что при x<x1 численные величины членов нашего ряда будут меньше ( во всяком случае не больше ) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии   по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.

Поэтому на основании признака сравнения делаем вывод, что ряд   сходится, а значит ряд   сходится абсолютно.

 

Таким образом, если степенной ряд  сходится в точке х1, то он абсолютно сходится в любой точке интервала длины 2  с центром в точке х = 0.

 

Следствие. Если при х = х1 ряд расходится, то он расходится для всех  .

 

Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что   ряд абсолютно сходится, а при всех  ряд расходится. При этом число Rназывается радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.

Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.

Радиус сходимости может быть найден по формуле: