
- •1.Звичайні др (основні поняття; задачі, що зводяться до др)
- •2. Др першого порядку. Теорема Коші
- •3. Деякі типи др: др 1 порядку з відкремленими і відокремлюваними зміними, однорідні др 1 пор, лінійні др 1 пор,рівняння Бернуллі
- •4.Др вищих порядків: загальний вигляд, існування розвязка задачі Коші, однорідні і неоднорідні лдр n-гопорядку
- •7) Лiнiйнозалежнi і лiнiйнонезалежнi системи функцiй. Визначник Вронського. Визначник Вронського для лiнiйно залежної системи функцiй.
- •8) Визначник Вронського: теореми, приклади.
- •9) Фcр олдр n-го порядку. Теорема про структyру загального розв'язку олдр. Формула Остроградського -Лiувiлля.
- •10) Теорема про структyру загального розв'язку нлдр n-го порядку. Принцип суперпозиції.
- •11) Метод Ейлера розв'язку олдр n-го порядку з постiйними коефiцiєнтами (випадок рiзних кopeнiв характеристичного рівняння).
- •12) Метод Ейлера розв'язку олдр n-го порядку з постiйними коефiцiєнтами (випадок кратних коренiв характеристичного piвняння).
- •13. Метод Ейлера розв’язку олдр n-го порядку з постійними коефіцієнтами (випадок комплексних коренів характеристичного рівняння).
- •14. Метод невизначених коефіцієнтів пошуку часткових розв’язків нлдр зі стандартною f(X):
- •15. Метод варіацій (Лагранжа) знаходження частинних розв’язків нлдр.
- •16. Числова послідовність та числові ряди: основні поняття (частинна сума, сума, приклади, геометричний ряд).
- •17. Необхідні умови збіжності числового ряду (наслідок).
- •18. Збіжність числового ряду та його залишку. Наслідок.
- •19. Критерій Коші. Гармонічний ряд.
- •20. Властивості збіжних чр(додавання, віднімання, множення на число). Збіжність чр та його залишку.
- •21. Ознака порівняння збіжності числових рядів. Наслідок.
- •22. Інтегральна ознака Коші. Узагальнений гармонічний ряд. Приклади.
- •23. Ознака Деламбера. Наслідок.
- •24. Радикальна ознака Коші.
- •25. Знакозмінні ряди. Ознака Лейбніца. Наслідок.
- •26.Абсолютно збіжні чр та їх властивості.
- •27.Умовно збіжні чр та їх властивості. Теорема Рімана. Приклади.
- •28.Функціональні послідовності та ряди. Основні поняття (область збіжності ,часткова сума , сума , приклад)
- •29.Рівномірно збіжні функціональні послідовності та ряди.
- •30.Теорема про неперервність суми рівномірно збіжного функціонального ряду.
- •31. Інтегрування функціонального ряду.
- •32. Диференційонування рівномірно збіжного ряду. Приклад.
- •33. Степеневі ряди. Теорема Абеля.
- •34. Поняття функції комплексної змінної. Стереографічна проекція. Границя та неперервність в точці функції комплексної змінної. Елементарні функції комплексної змінної.
- •4.5. Логарифмічнафункція
4.5. Логарифмічнафункція
Логарифмічна функція комплексної змінної визначається як обернена до показникової:
Комплексне
число
 називається натуральним
логарифмом
ненульового комплексного числа
,
якщо виконується рівність
називається натуральним
логарифмом
ненульового комплексного числа
,
якщо виконується рівність
 .
.
Нехай
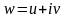 ;
;
 .
Тоді за означенням
.
Тоді за означенням
 ;
;
 ;
;
 ;
;
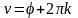 ,
,
 .
.
Звідси
 – звичайний натуральний логарифм
додатного числа
– звичайний натуральний логарифм
додатного числа
 ;
;
 – вся множина значень аргументу
ненульового комплексного числа
– вся множина значень аргументу
ненульового комплексного числа
 .
.
Отже,
 .
.
35.Похідна функції комплексної змінної. Необхідна і достатня умова аналітичності функції (доведення необхідності). Поняття похідної функції в точці та області. Геометричний зміст модуля та аргументу похідної.
Озн.
Похідною ф-ією
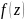 в точці z
наз-ся границя відношення приросту ф-ії
∆
=
в точці z
наз-ся границя відношення приросту ф-ії
∆
=
 до приросту аргумента ∆
до приросту аргумента ∆ при ∆
→0
при ∆
→0
 =
=

Теор.
Якщо ф-ії U(x,y)
iV(x,y)
диференційовані в т. ( ,
,
 ),
то ф-ія W=f(z)=U(x,y)+iV(x,y)
диференційована в т
+і
тоді и тільки тоді, коли в цій т. виконуються
умови Коші-Рімана:
),
то ф-ія W=f(z)=U(x,y)+iV(x,y)
диференційована в т
+і
тоді и тільки тоді, коли в цій т. виконуються
умови Коші-Рімана:
 ;
;

Доведення.
Необхідність.
Нехай функція
в фіксованійточці
маєпохідну ,
,
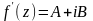 .
Звідси
.
Звідси
 ,
,
де
 –
нескінченно мала функціяпри
–
нескінченно мала функціяпри ,
тому їїдійсна
,
тому їїдійсна і
уявна
і
уявна частини
також нескінченно малі.
частини
також нескінченно малі.
Підставимо вирази
 ;
;
;
;
 ;
;
у співвідношення для приросту функції і відділимо дійсну та уявну частини
 ;
;
 ;
;
 .
.
Останні дві рівності
показують, щофункції і
і
 диференційовні
в точці
диференційовні
в точці ,
причому
,
причому
 ;
;
 .
.
Звідси .
.
А ргумент
похідної в комплексно значній ф-ії
дійсної змінної дорівнює куту нахилу
кривої L
по відношенню до дійсної осі.
ргумент
похідної в комплексно значній ф-ії
дійсної змінної дорівнює куту нахилу
кривої L
по відношенню до дійсної осі.
локальний
коефіцієнт розтягу в точці
 під дією аналітичної функції
в усіх напрямах однаковий і дорівнює
модулю похідної
під дією аналітичної функції
в усіх напрямах однаковий і дорівнює
модулю похідної

36.Гармонійні функції. Спряжені гармонійні функції. Відновлення аналітичної функції за її дійсною чи уявною частиною.
Функція
U(x,y)
– гармонійна, якщо задовольняє рівняння
Лапласа

Гармонійні функції, що є дійсною та уявною частинами однієї аналітичної функції називаються спряженими гармонійними функціями.
Для відновлення аналітичної функції використовуються умови Коші-Рімана:
;

45. Поняття лишку та йогообчислення в особливих точках

46. Теорема Коші про лишки
47.Обчислення інтегралів за допомогою лишків

48. Поняття функції оригіналу та основні поняття властивості про Лапласа. Приклади(n(t) – функції Хевісаїда, е^??). Теорема про існування зображення по Лапласу. Теорема Мельдіна.




49. Перетворення Лапласа. Властивості зображення по Лапласу(лінійність та подібність). Приклади: sin(wt), cos(wt), sh(wt), ch(wt).


50. Перетворення Лапласа. Диференціювання оригіналу та зображення. Приклади зображення степеневої функції: t^n, n є N/



51. Перетворення Лапласа. Інтегрування оригіналу та зображення.

52. Перетворення Лапласа. Теореми про запізнення та зміщення. Зображення ступеневої(східчастої) функції.


53. Згортка функції, її властивості. Теорема Бореля. Інтеграл Дюамеля.


5 4.
Розв*язування ЛОДР зі сталими коефіцієнтами
та системи таких рівнянь за
допомогоюопераційногочислення.
4.
Розв*язування ЛОДР зі сталими коефіцієнтами
та системи таких рівнянь за
допомогоюопераційногочислення.


55. Інтегро-диференціальні рівняння Вольтера І і ІІ роду. Розв*язування їх за допомогою Лапласа.
Рівняння Вольтера
Інтегральне рівняння Вольтерра — інтегральне рівняння спеціального виду. Розрізняють рівняння Вольтерра двох типів:
лінійне першого роду
![]()
та лінійне другого роду
![]()
Де
![]() — відомі функції,
x(t) — функція, яку потрібно знайти, λ —
комплексний параметр. K(t,s) називається
ядром інтегрального рівняння, f(t) —
вільним членом.
— відомі функції,
x(t) — функція, яку потрібно знайти, λ —
комплексний параметр. K(t,s) називається
ядром інтегрального рівняння, f(t) —
вільним членом.
Всяке рівняння Вольтера з неперервним ядром при довільному комплексному параметрі ( )має єдиний розвязок, що представляється у вигляд рівномірно збіжного ряду Неймана.
x(t) = x0(t) + x1(t) + λ2x2(t) + ...
де
![]()
