1.Звичайні др (основні поняття; задачі, що зводяться до др)

Звичайні диференціальні рівняння — це рівняння виду F(t,x,x',x'',...,x⁽ⁿ⁾) = 0, де x = x(t) — невідома функція (можливо, вектор-функція; в такому випадку часто говорять про систему диференціальних рівнянь), що залежить від змінної часу t, штрих означає диференціювання по t. Число n називається порядком диференціального рівняння.Розв'язком (або рішенням) диференціального рівняння називається функція, що диференціюється n разів, і задовольняє рівнянню в усіх точках своєї області визначення. Зазвичай існує ціла множина таких функцій, і для вибору одної з розв'язок потрібно накласти на неї додаткові умови: наприклад, вимагати, щоб рішення приймало в певній точці певне значення.

Для розв’язання багатьох питань науки і техніки потрібно вміти знаходити невідомі функції, що описують ті чи інші явища і процеси, якщо задано співвідношення, які встановлюють зв’язок між цими функціями, їхніми похідними та незалежними змінними. Такі співвідношення і називають диференціальними рівняннями. 

2. Др першого порядку. Теорема Коші

3. Деякі типи др: др 1 порядку з відкремленими і відокремлюваними зміними, однорідні др 1 пор, лінійні др 1 пор,рівняння Бернуллі

4.Др вищих порядків: загальний вигляд, існування розвязка задачі Коші, однорідні і неоднорідні лдр n-гопорядку

7) Лiнiйнозалежнi і лiнiйнонезалежнi системи функцiй. Визначник Вронського. Визначник Вронського для лiнiйно залежної системи функцiй.

Функції y₁(x), y₂(x), ..., y_n (x), визначені на відрізку [a; b], називаються лінійно залежними на [a; b], якщо існують постійні α₁, α₂, ..., α_n, не рівні нулю одночасно і такі, що α₁y₁(x) + α₂y₂(x) + ... + Α_ny_n(x) = 0 для всіх x з відрізка [a; b]. В іншому випадку функції y₁ (x), y₂ (x), ..., y_n(x) називаються лінійно незалежними. Функції y₁(x), y₂(x), ..., y_n(x) лінійно залежні на відрізку [a; b] тоді і тільки тоді, коли хоча б одна з них є лінійною комбінацією інших на цьому відрізку. Вектор-функції Y₁(x), Y₂(x), ..., Y_n(x),

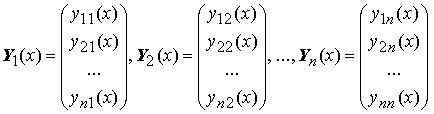
називаються лінійно залежними на відрізку [a; b], якщо існують постійні α₁, α₂, ..., α_n, не рівні нулюодночасно і такі, що α₁ Y₁(x) + α₂ Y₂(x) + ... + Α_nY_n(x) = 0 для всіх x з відрізка [a; b]. В іншому випадку функції Y₁(x), Y₂(x), ..., Y_n(x) називаються лінійно незалежними.

Визначник Вронського (Вронскіан) — визначник, складений із функцій та похідних.Для n фукнцій визначник Вронського будується з використанням похідних до n-1 порядку.

Теорема про вронскіан лінійно залежної системи функцій. 

Якщо система функцій y₁(x), y₂(x), ...,y_n(x) лінійно залежна на інтервалі (a, b), то вронскіан цієї системи тотожно дорівнює нулю на цьому інтервалі. Доведення. 

Якщо функції y₁(x), y₂(x), ...,y_n(x) лінійно залежні на інтервалі (a, b), то знайдуться числа,з яких хоча б одне відмінно від нуля, такі що для (1).

Продифференцируем по x рівність (1) n - 1 раз і складемо систему рівнянь

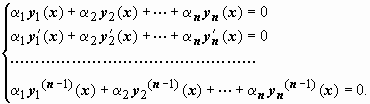
Будемо розглядати цю систему як однорідну лінійну систему алгебраїчних рівнянь відносно . Визначник цієї системи - визначник Вронського. При ця система має нетривіальний розв’язок . А отже, в кожній точці її визначник рівний 0.

Отже, W(x)=0 , тобто на (a, b).

8) Визначник Вронського: теореми, приклади.

Визначник Вронського (Вронскіан) — визначник, складений із функцій та похідних.Для n фукнцій визначник Вронського будується з використанням похідних до n-1 порядку.

Теорема про вронскіан лінійно залежної системи функцій. 

Якщо система функцій y₁(x), y₂(x), ...,y_n(x) лінійно залежна на інтервалі (a, b), то вронскіан цієї системи тотожно дорівнює нулю на цьому інтервалі. Доведення. 

Якщо функції y₁(x), y₂(x), ...,y_n(x) лінійно залежні на інтервалі (a, b), то знайдуться числа,з яких хоча б одне відмінно від нуля, такі що для (1).

Продифференцируем по x рівність (1) n - 1 раз і складемо систему рівнянь

Будемо розглядати цю систему як однорідну лінійну систему алгебраїчних рівнянь відносно . Визначник цієї системи - визначник Вронського. При ця система має нетривіальний розв’язок . А отже, в кожній точці її визначник рівний 0.

Отже, W(x)=0 , тобто на (a, b).

Для лінійного диференційного рівняння другого порядку

Для однорідного лінійного диференційного рівняння другого порядку у формі

визначник Вронського, складений із лінійно незалежних розв'язків рівняння визначається функцією g(x).

Нехай y₁(x) та y₂(x) - два лінійно незалежні розв'яки, тобто

Домножаючи перше рівняння на y2(x) а друге на y1(x) і віднімаючи отримуємо

або

.

Цю властивість можна використати для знаходження другого лінійно незалежного розв'язку рівняння, якщо один вже відомий. Рівняння для другого розв'язку є рівнянням першого, а не другого порядку.

Приклади

• Переконаємося, що вронскіан лінійно-залежних функцій 1, x², 3 + 2x² дорівнює нулю:

• Перевіримо тепер лінійну незалежність функцій 1,x,x³

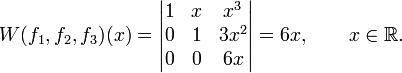
Є точки, де вронскіан відмінний від нуля (у нашому випадку це будь-яка точка, крім x = 0). Тому на будь-якому проміжку ці функції будуть лінійно незалежними.