17. Необхідні умови збіжності числового ряду (наслідок).

Якщо числовий ряд _nзбіжний, то його загальний член ( _n= 0) прямує до нуля.

Доведення. Позначимо через Sсуму ряду.

S = _n S_n = U₁ + … + U_n S_n-1 = U₁ + … + U_{n-1 n-1} = S

_n - _n-1 = S – S

_n - S_n-1) = 0 _n= 0, що і треба довести.

Наслідок: Якщо _n 0 , то ряд розбіжний.

18. Збіжність числового ряду та його залишку. Наслідок.

Те ж саме + Числовий ряд, одержаний із даного відкиданням його перших n членів, називається n-им залишком числового ряду.

U₁ + U₂ + … + U_р - р-ий залишок ЧР, р

Зі збіжності ЧР випливає і збіжність будь-якого його залишку.

Із розбіжності будь-якого залишку ЧР випливає і розбіжність самого ряду.

19. Критерій Коші. Гармонічний ряд.

Критерій Коші збіжності числового ряду.

Для того, щоб числовий ряд був збіжним необхідно і досить щоб

Доведення слідує з критерію Больцано-Коші збіжності числової послідовності, яку застосуємо до { } даного ряду. Для збіжності { } за критерієм Коші необхідно і досить

Гармонический ряд - числовой ряд

Каждый член такого ряда, начиная со второго, является гармоническим средним двух соседних - этим объясняется название. Отдельные члены ряда стремятся к нулю, но его сумма расходится.

Обобщённый гармонический ряд сходится при α > 1 и расходится при α ≤ 1.

20. Властивості збіжних чр(додавання, віднімання, множення на число). Збіжність чр та його залишку.

Властивості збіжних числових рядів:

1. Якщо збіжний, то const: також збіжний і його сума

2. , збіжні, їх суми S і , то то

3. Якщо збігається, то збігається будь який його залишок і навпаки.

r-й залишок числового ряду:

З теореми слідує, що збіжність ч.р. не порушиться, якщо відкинути скінченне число перших членів.

21. Ознака порівняння збіжності числових рядів. Наслідок.

Якщо для членів додатних числових рядів , виконується нерівність , , то:

1. із збіжності числового ряду слідує збіжність числового ряду .

2. із розбіжності числового ряду слідує розбіжність числового ряду .

Доведення: збіжність означає обмеженість послідовності його частинних сум { }, . За умовою теореми частинні суми числового ряду задовольняють умову , – монотонно зростає, обмежена зверху, за теоремою Веєрштраса

Наслідок – гранична теорема порівняння. Якщо для додатних числових рядів , , ; , то для :

1. при , то із збіжності слідує збіжність .

2. при , то із розбіжності слідує розбіжність .

3. при , то 2 ряди ведуть себе однаково.

22. Інтегральна ознака Коші. Узагальнений гармонічний ряд. Приклади.

Якщо f(x) визначена і неперервна при , невід’ємна, де і монотонно спадна, то ч.р. такий що , і збігається то і ряд збігається, якщо інтеграл розбіжний – то розбіжний і ряд.

Обобщённый гармонический ряд сходится при α > 1 и расходится при α ≤ 1.

Приклад:

При – ряд збіжний,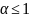 розбіжний.

23. Ознака Деламбера. Наслідок.

Якщо для додатного ряду , , то ряді збіжний. При числовий ряд розбіжний.

Доведення: базується на порівнянні з геометричним числовим рядом

, при q<1 цей ряд збіжний як геометричний ряд, звідси слідує збіжність ряду за ознакою порівняння.

Наслідок: якщо для додатного числового ряду існує , то при q<1 – числовий ряд збіжний, при q>1 ряд розбіжний, при q=1 ряд збіжний чи розбіжний.