9) Фcр олдр n-го порядку. Теорема про структyру загального розв'язку олдр. Формула Остроградського -Лiувiлля.

Фундаментальна система розв’язків та ії існування.

Означення. Сукупність n розв’язків диференціального рівняння, визначених і лінійно незалежних на (a,b) називається фундаментальною системою розв’язків .

З попереднього випливає для того , щоб система n розв’язків диференціального рівняння була фундаментальною системою розв’язків необхідно і достатньо, щоб вронскіан цих розв’язків був відмінний від нуля хоч в одній точці інтервалу неперервності коефіцієнтів диференціального рівняння. Всі ці розв’язки повинні бути бути ненульовими .

Теорема (про існування ФСР). Якщо коефіцієнти диференціального рівняння являються неперервними на (a,b) , то існує фундаментальна система розв’язків на цьому інтервалі.

Доведення . Візьмемо точку  (a,b) і побудуємо, використовуючи метод Пікара , розв’язки

 з початковими умовами  ;

------------- // ---------------  ;

... ------------- // --------------- ... ... ... ....

 ------------- // ---------------  .

Очевидно , що  , отже побудовані розв’язки лінійно незалежні . Теорема доведена.

З методу побудови лінійно незалежних функцій випливає, що таких функцій можна побудувати безліч.

Побудована система розв’язків називається нормованою в точці  .

Для будь-якого диференціального рівняння існує тільки одна фундаментальна система розв’язків , нормована по моменту  .

Теорема (про структуру загального розв’язку ОЛДР). Якщо розв’язки ОЛДР утворюють на [a;b]ФСР, тоді загальний розв’язок рівняння на [a;b] можна представити у вигляді

Покажемо, що для довільної початкової умови знайдуться спільні константи с₁,…,с_nпри підстановці яких в (1), отримаємо розв’язок задачі Коші. Підставляючи в кожну умову замість у систему (1) отримаємо систему:

Визначником цієї системи є визначник Вронського: W(x0) 0. Звідси слідує, що система має розв’язки.

Формула Остроградського-Ліувілля:

Оскільки максимальне число лінійно незалежних розв’язків дорівнює , то система буде залежною і , тобто

Формула:

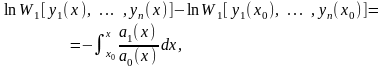
або

Вона називається формулою Остроградського - Ліувілля. Зокрема, якщо рівняння має вид

то формула запишеться у вигляді

10) Теорема про структyру загального розв'язку нлдр n-го порядку. Принцип суперпозиції.

Теорема:Розглянемо тепер неоднорідне лінійне рівняння другого порядку:

y`` + a₁(x)y` + a₂(x)y=f(x),(1)

Загальним розв`язком рівняння є сума його довільного частинного розв`язку і загального розв`язку відповідного однорідного рівняння.

Нехай у*(х) - частинний розв`язок рівняння (1), а у**(х)= c<sub>1</sub>y<sub>1</sub>(х) + c<sub>2</sub>у<sub>2</sub>(х) - загальний розв`язок рівняння.

Переконаємось, що функція у(х) = у*(х)+у**(х) (2) - розв`язок рівняння (1). Підставляючи функцію (2) в рівняння (1), дістанемо

y*``(х) + у**``(x) + а₁(х)(у*`(х) + у**`(х)) + а₂(х)(у*(х)+у**(х))= = {y*``(х) + а<sub>1</sub>(х)у*`(х) + а<sub>2</sub>(х)у*(х)} + [у**``(х) + а₁(х)у**`(х) + а₂(х)у**(х)] = f(x).

Оскільки вираз у квадратних дужках дорівнює нулю, а у фігурних - функції f(х), то функція (2) є розв`язком рівняння (1).

Принцип суперпозиції.

Якщо - розв’язки лінійних неоднорідних диференціальних рівнянь

, ,

то з довільними сталими буде розв’язком лінійного неоднорідного рівняння

Дійсно, нехай - розв’язки відповідних неоднорідних рівнянь, тобто

Склавши лінійну комбінацію з рівнянь і їхніх правих частин з коефіцієнтами одержимо

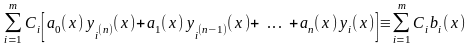
або, перегрупувавши, запишемо

що і було потрібно довести.