
- •Основные допущения и гипотезы сопротивления материалов
- •Расчетная схема. Классификация расчетных схем по геометрическому признаку
- •Внешние силы. Силы массовые и поверхностные. Сосредоточенные силы
- •Принципы сопротивления материалов: неизменяемости начальных размеров, независимости действия сил, Сен-Венана.
- •Механические характеристики материалов
- •Внутренние силы. Метод сечений. Внутренние силовые факторы
- •Метод сечений.
- •Внутренние силовые факторы.
- •Напряжения и деформации Напряжение.
- •Растяжение и сжатие. Удлинения и деформации при растяжении и сжатии
- •Коэффициенты запаса прочности и допускаемые напряжения
- •Закон Гука при растяжении и сжатии
- •Определение перемещений при растяжении (сжатии)
- •Закон парности касательных напряжений (из напряжений по косым площадкам)
- •Расчёты на прочность (проектировочный, проверочный, определение несущей способности)
- •Напряженное состояние при растяжении и сжатии (напряжения по косым площадкам)
- •Статически неопределимые системы, работающие на растяжение и сжатие
- •Свойства статически неопределимых систем.
- •Расчет статически неопределимых систем, работающих на растяжение и сжатие за пределами упругости
- •Особенности расчета за пределами упругости.
- •Предельное состояние системы, работающей на растяжение.
- •Чистый сдвиг. Закон Гука при чистом сдвиге. Связь между модулем упругости и модулем сдвига
- •Кручение стержней круглого поперечного сечения
- •Угловое перемещение при кручении и условие жёсткости при кручении (определение касательных напряжений при кручении)
- •Расчет полых валов
- •Кручение стержней прямоугольного поперечного сечения
- •Моменты сопротивления плоских сечений (прямоугольное, круглое, составные сечения)
- •Кручение тонкостенных стержней открытого профиля
- •Кручение тонкостенных стержней замкнутого профиля
- •Статически неопределимые задачи кручения
- •Геометрические характеристики поперечных сечений. Статические моменты и моменты инерции и их свойства.
- •Статические моменты.
- •Преобразование моментов инерции при параллельном переносе осей
- •Моменты инерции простейших фигур (прямоугольник, треугольник, круг)
- •Преобразование моментов инерции при повороте осей
- •Главные оси и главные моменты инерции
- •Изгиб. Внутренние силовые факторы при изгибе
- •Дифференциальные зависимости при изгибе
- •Напряжения при чистом изгибе
- •Расчеты на прочность при изгибе. Рациональные типы сечений при изгибе
- •Напряжения при поперечном изгибе. Формула Журавского
- •Косой изгиб
- •Напряжения при косом изгибе.
- •Внецентренное растяжение и сжатие
- •Перемещения при изгибе. Дифференциальное уравнение изогнутой оси
- •Интегрирование уравнения изогнутой оси по методу начальных параметров
- •Теорема о работе силы, приложенной к линейно упругой системе
- •Теорема Кастилиано
- •Метод Мора. Интеграл Мора
- •Вычисление интеграла Мора по методу Верещагина
- •Кинематический анализ плоских стержневых систем. Статически неопределимые рамы и балки
- •Метод сил. Уравнения метода сил.
- •Использование симметрии и косой симметрии при расчете рам и балок
- •Правило:
- •Расчет статически неопределимых балок
- •Проверка правильности раскрытия статической неопределимости.
Статические моменты.
На основании теоремы Вариньена (о моменте равнодействую-
щей) можно записать
![]()
где
![]() и
и
![]() - координаты центра тяжести площади.
Отсюда мы имеем
- координаты центра тяжести площади.
Отсюда мы имеем
прием для отыскания
центра тяжести площади:
![]()
Ось, относительно которой статический момент равен нулю, называют центральной (естественно, что она проходит через центр
тяжести фигуры).
Если мы имеем дело с составной фигурой, т.е. фигурой состоящей из частей, для каждой из которой мы знаем площадь и координаты центра тяжести, то статические моменты можно найти:
![]()
где
![]() - соответственно площадь и координаты
центра тяжести фигуры составляющей.
- соответственно площадь и координаты
центра тяжести фигуры составляющей.
30)
Преобразование моментов инерции при параллельном переносе осей
Пусть
![]() - центральные оси для данной фигуры, а
- центральные оси для данной фигуры, а
![]() и
и
![]() - произвольные оси параллельные осям
и
.
- произвольные оси параллельные осям
и
.
Найдем моменты инерции для осей и , через, как выражаются, “старые” моменты инерции относительно осей и .
С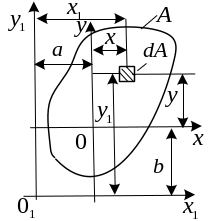 вязь
между “новыми” и “старыми” координатами
произвольной элементарной площадки
будут выглядеть
вязь
между “новыми” и “старыми” координатами
произвольной элементарной площадки
будут выглядеть
![]()
где
![]() и
и
![]() - координаты старого центра в новых
осях. Подставляя эти выражения в формулы
для моментов инерции, и учитывая, что
оси
- центральные получаем:
- координаты старого центра в новых
осях. Подставляя эти выражения в формулы
для моментов инерции, и учитывая, что
оси
- центральные получаем:
![]()
Проделывая аналогичные выкладки и для других моментов, получаем следующий закон преобразования моментов:
![]() ;
;
![]() ;
;
![]()
Первыми двум выражениям можно придать словесную формулировку: момент инерции относительно какой-либо оси равняется моменту относительно оси центральной параллельной данной плюс площадь на квадрат расстояния между осями.
31)
Моменты инерции простейших фигур (прямоугольник, треугольник, круг)
а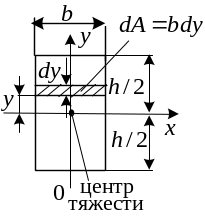 )
Момент инерции для прямоугольника
относительно центральной оси:
)
Момент инерции для прямоугольника
относительно центральной оси:
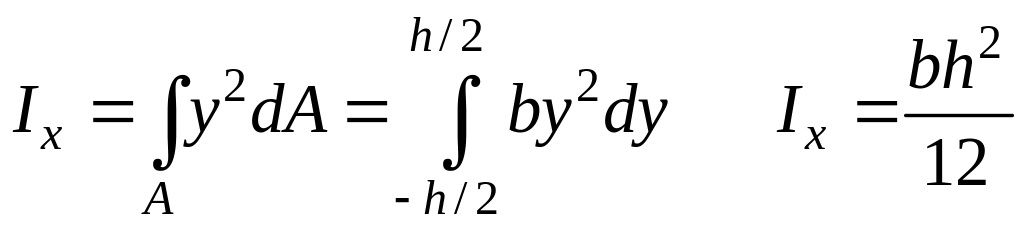
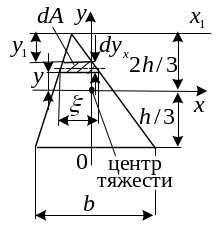
б) Треугольник
Момент инерции относительно оси
:
![]()
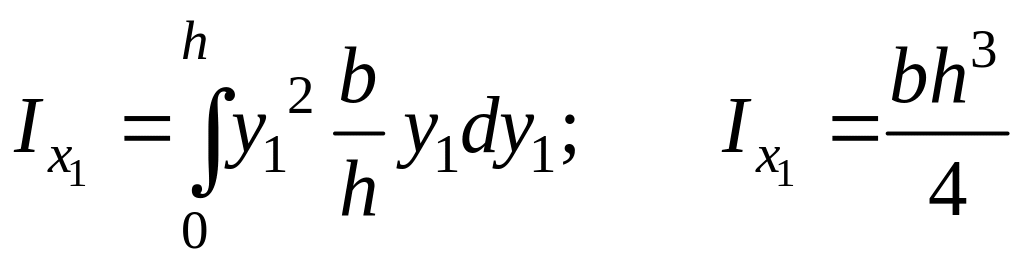
Используя формулу преобразования
момента инерции при параллельном
переносе осей, получаем выражение для
центрального момента инерции:
![]()
в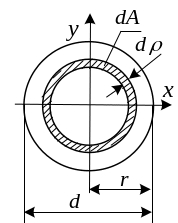 )
Круг
)
Круг
Из соображений симметрии заключаем,
что все центральные оси обладают равными
моментами инерции. Поэтому
![]() Найдем вначале полярный момент инерции:
Найдем вначале полярный момент инерции:
![]()
![]() или через диаметр:
или через диаметр:
![]()
г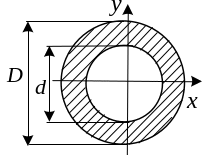 )
Кольцевое сечение.
)
Кольцевое сечение.
![]()
обозначив , имеем
32)
Преобразование моментов инерции при повороте осей
Пусть х, у произвольные площади сечения площадью F, а оси , получены из них поворотом на угол . Найдем моменты
инерции относительно осей , через “старые” моменты инерции
относительно осей , через “старые” моменты инерции относительно осей х, у.
Связь между координатами известна из курса аналитической геометрии
![]() ;
;
![]() .
.
Вычислим момент инерции
![]()
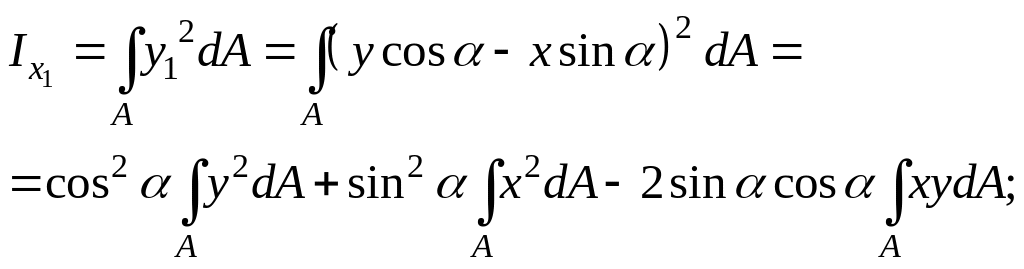

Входящие в это выражение, интегралы
представляют собой моменты инерции
относительно осей
![]()
![]()
Учитывая известные тригонометрические тождества:
![]()
![]()
![]() переходим к функциям угла
.
переходим к функциям угла
.
Если проделать эту процедуру и для
![]() то получим следующие формулы преобразования
моментов инерции при повороте
то получим следующие формулы преобразования
моментов инерции при повороте
координатных осей:
![]()
![]()
![]()
Складываем два первых уравнения, получаем
![]()
т.е. сумма осевых моментов инерции инвариантна по отношению к повороту осей (на самом деле, она ведь равна полярному моменту инерции, а последний зависит лишь от полюса, а не от положения осей ).
33)
