
- •1. Основные определения: информация, сообщение, система связи, сигнал, алфавит.
- •2. Функциональная система цифровой системы связи.
- •3. Преимущества и недостатки цифровой связи
- •4.Четырехуровневая коммуникационная система
- •5. Эталонная модель (osi): стек протоколов
- •6. Уровни модели взаимодействия открытых систем osi
- •Блочная диаграмма типичной системы цифровой связи от источника к передатчику
- •Блочная диаграмма типичной системы цифровой связи от приемника к потребителю информации
- •9. Отображение цифрового сигнала в виде аналоговой функции времени
- •10. Сигнал как реализация процесса. Классификация процессов
- •12. Полигармонические и почти периодические процессы
- •13. Определение случайного процесса
- •14. Процесс стационарный в широком смысле
- •15. Процесс стационарный в узком смысле
- •16. Случайные эргодические процессы, гауссов процесс
- •17. Процессы авторегрессии
- •18. Ковариационная и корреляционная матрицы случайного процесса, автоковариационная и автокорреляционная функции
- •19. Оценивание ковариационной и корреляционной матриц случайного процесса и автоковариационной и автокорреляционной функций
- •20. Случайные нестационарные процессы, характеристики случайных процессов
- •21. Классификация шумов в системах связи.
- •22. Определение спектральной плотности мощности. Теорема Винера-Хинчина.
- •23. Непрерывное преобразования Фурье
- •24. Финитное преобразование Фурье
- •25. Дискретное преобразование Фурье (дпф).
- •26. Свойства дпф.
- •27. Оценивание спектральной плотности с помощью дпф
- •28. Модель белого шума.
- •29. Линейные системы с постоянными параметрами.
- •Характеристики линейных систем с постоянными параметрами.
- •31. Последовательное включение систем с постоянными параметрами.
- •32. Связь спектральных плотностей входного и выходного процессов линейной системы с постоянными параметрами.
- •3 5. Узкополосные и широкополосные сигналы.
- •36. Критерии определения ширины полосы.
- •Форматирование текстовой информации в системах dcs.
- •38. Теорема о дискретном представлении. Критерий Найквиста. Инженерный критерий Найквиста.
- •Дискретизация с помощью идеальных единичных импульсов (идеальная дискретизация).
- •Естественная дискретизация.
- •41.Дискретизация по методу «выборка-хранение».
- •42.Квантование амплитуды и характеристики.
- •45.Шум квантования.
- •46.Импульсно кодовая модуляция квантованных выборок аналогового сигнала.
- •47.Кодирование источников определения.
- •48.Дискретные источники и их характеристики.
- •49.Типы дискретных источников.
- •50.Свойства кодов.
- •51. Показатели кодирования
- •52. Кодирование источников без памяти: код шеннона-фано
- •54. Кодирование источников с памятью: методы подавления нулей и групповое кодирование
- •55. Кодирование источников с памятью: методы подстановки образцов и дифференциальное сжатие
- •56. Униполярные и биполярные сигналы pcm
- •57. Сигналы рсм в кодировке nrz (nrz-l, nrz-m, nrz-s)
- •58. Кодировки nrz-ami и rz-ami
- •59. Фазовое кодирование
- •60. Кодирование модуляцией задержки
- •61. Многоуровневое кодирование рсм. Достоинства и недостатки
- •62. Искажение сигналов шумом awgn
- •63. Межсимвольная интерференция
- •64. Обобщенная схема передачи узкополосного сигнала
- •65. Основные этапы демодуляции/обнаружения
- •68. Униполярная передача двоичных сигналов
- •69. Биполярная передача двоичных сигналов
- •70. Эквивалентная модель системы dcs
- •71. Импульсы Найквиста
- •72. Компенсация искажений с помощью выравнивания
- •73. Виды выравнивания и типы эквалайзеров.
- •74. Дискретный канал без памяти
- •75. Теорема кодирования канала
- •76. Теорема о пропускной способности канала
- •Зачем нужна широкополосная модуляция?
- •78, 79. Амплитудная и частотная модуляция (ask и fsk)
- •80. Частотная манипуляция и бинарная частотная манипуляция
- •81. Бинарная фазовая манипуляция, квадратурная фазовая манипуляция
- •82. Амплитудно-фазовая манипуляция (арк)
- •83. Определение полосовой демодуляции и ее виды
- •84. Ресурс связи и способы его распределения
- •85. Сигналы, ортогональные во времени и по частоте
- •86. Уплотнение/множественный доступ с частотным разделением
- •87. Множественный доступ с временным разделением
24. Финитное преобразование Фурье
______________________СМ. ПУНКТ 23__________________________
На практике
анализируемый сигнал
задается на интервале конечной длины
![]() ;
обозначим этот интервал через
;
обозначим этот интервал через
![]() .
Преобразование Фурье ограниченной
реализации имеет вид
.
Преобразование Фурье ограниченной
реализации имеет вид
![]() . (5.7)
. (5.7)
Преобразование, определяемое формулой (5.7) называется финитным преобразованием Фурье.
Чтобы получить
периодическую функцию времени с периодом
,
положим, что реализация
непрерывно повторяется. Разлагая такую
функцию в ряд Фурье, находим
![]() , (5.8)
, (5.8)
где все частоты
![]() кратны основной частоте
кратны основной частоте
![]() .
Следовательно, приращение частоты между
последовательными значениями
и
.
Следовательно, приращение частоты между
последовательными значениями
и
![]() равно
равно
![]() .
Коэффициенты ряда (5.8) находятся по
формулам
.
Коэффициенты ряда (5.8) находятся по
формулам
![]() .
(5.9)
Из формулы
(5.7) следует, что
.
(5.9)
Из формулы
(5.7) следует, что
![]() . (5.10)
. (5.10)
Таким образом,
величина
![]() определяет значения коэффициентов
определяет значения коэффициентов
![]() и, следовательно, ординаты
при всех t.
Это справедливо
при условии, что функция
периодична с периодом
.
Очевидно, значения
это значения финитного преобразования
Фурье, определенные для частот
и, следовательно, ординаты
при всех t.
Это справедливо
при условии, что функция
периодична с периодом
.
Очевидно, значения
это значения финитного преобразования
Фурье, определенные для частот
![]() ,
,
![]()
25. Дискретное преобразование Фурье (дпф).
Предположим, что
непрерывная реализация
представлена N
эквидистантными
значениями с интервалом дискретизации
.
Поскольку при рассмотрении финитного
преобразования Фурье мы задавали
интервал определения
как
,
моменты
![]() удобно индексировать, начиная с
удобно индексировать, начиная с
![]() .
Тогда последовательность отсчетов
запишется в виде
.
Тогда последовательность отсчетов
запишется в виде
![]() ,
,
![]() .
.
Дискретная аппроксимация интеграла (по методу прямоугольников) в формуле при произвольном значении f есть
![]() . (5.11)
. (5.11)
Для расчета спектра выбираем дискретные значения частоты
![]() ,
,
![]() . (5.12)
. (5.12)
Формула (5.11) дает на этих частотах следующие составляющие Фурье
![]() ,
, (5.13)
,
, (5.13)
причем интервал
внесен в значение
![]() ,
чтобы избавиться от множителя перед
знаком суммы. Подставив в соотношение
(5.13) выражение для
из (4.12), получим формулу для дискретного
преобразования Фурье
,
чтобы избавиться от множителя перед
знаком суммы. Подставив в соотношение
(5.13) выражение для
из (4.12), получим формулу для дискретного
преобразования Фурье
![]() ,
. (5.14)
,
. (5.14)
Внимание, это
важно!
Дискретное преобразование Фурье (ДПФ)
применяется для оценивания спектра,
задаваемого соотношением (5.1). Частоты,
определяемые соотношением (5.12), (точки
на оси частот) называются опорными
частотами
ДПФ, а
промежутки
![]() (интервалы частотной оси) между
последовательными частотами ДПФ –
бинами ДПФ.
Формула (4.14) часто записывается в виде
(интервалы частотной оси) между
последовательными частотами ДПФ –
бинами ДПФ.
Формула (4.14) часто записывается в виде
![]() ,
,
где ДПФ{} оператор ДПФ.
26. Свойства дпф.
Последовательность
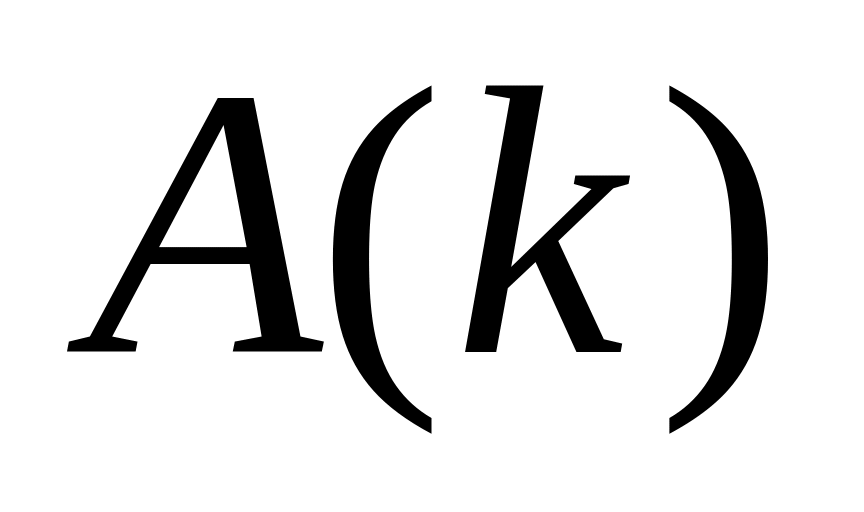 периодически повторяется через N
значений:
периодически повторяется через N
значений:
![]() ,
где
,
где
![]() .
(5.15)
.
(5.15)
ДПФ действительных временных рядов
 обладает свойством комплексной
симметрии, которое записывается в виде
обладает свойством комплексной
симметрии, которое записывается в виде
![]() ,
,
![]() .
.
Учитывая (5.15), последнее соотношение можно представить как
![]() ,
, (5.16)
,
, (5.16)
другими словами,
частоты выше
![]() можно рассматривать (теоретически) как
отрицательные.
можно рассматривать (теоретически) как
отрицательные.
Значение
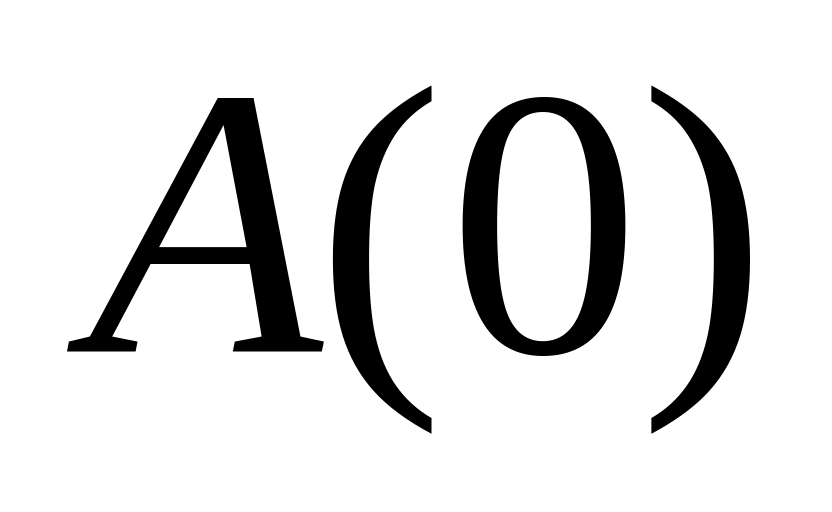 для действительных последовательностей
равно
для действительных последовательностей
равно
![]() , (5.17)
, (5.17)
![]() , (5.18)
, (5.18)
где
![]()
выборочное среднее величин
.
выборочное среднее величин
.
Свойство линейности ДПФ формулируется аналогично (5.5), т. е.
![]() ,
,
где a
и b
постоянные коэффициенты,
![]() и
и
![]()
два разных сигнала одинаковой длины.
два разных сигнала одинаковой длины.
.(5.5)
