Нескінченна диференційовність добутку функцій і складної функції

О1. Функцію називають нескінченно диференційовного на множині якщо для будь-якого значення аргумента з цієї множини і для кожного натурального числа функція має похідну n-го порядку.

Лема 1. (про нескінченну диференційовність добутку функцій)

Якщо дві функції нескінченно диференційовні на множині, то їх добуток є функцією нескінченно диференційовною на цій множині

З теореми Лейбніца про похідну n-го порядку від добутку функцій випливає

Лема 2(про нескінченну диференційовність складної функції)

Якщо функція нескінченно диференційовна на множині X, функція нескінченно диференційовна на образі множини X, то складна функція нескінченно диференційовна на множині X

Доведення

З умов

Нерівність між середніми

О1. Середніми степеневими n додатних чисел порядку р називаються суми

Якщо - середнє арифметичне).

Якщо - середнє квадратичне).

Якщо - середнє гармонійне).

Використовуючи правила Лопіталя і означення неперервної функції, одержимо

Т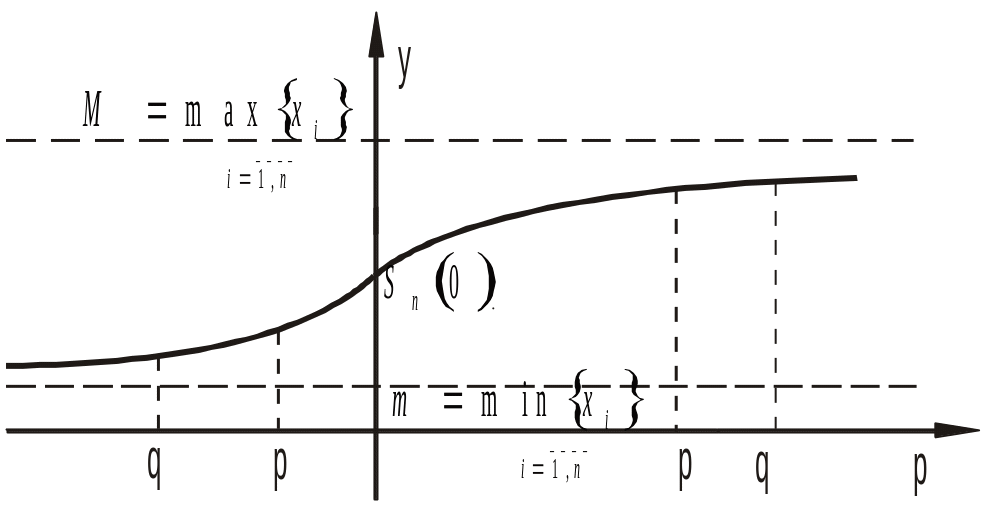 еорема 1 (про властивості функції )

Середні степеневі порядку р є нескінченно диференційовною функцією на множині , неперервною на множині R, строго зростаючою на множині R, якщо точа б два числа нерівні між собою. Границя середніх степеневих при дорівнює максимальному з чисел і при дорівнює мінімальному з чисел. Середнє степеневе стале на множині R, тоді і тільки тоді коли всі числа рівні між собою і рівні цій сталій тобто:

Доведення. Використаємо означення середнього геометричного і неперервності функції в точці. Якщо

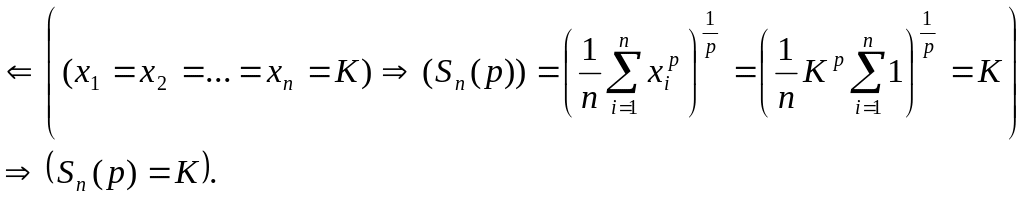
Наслідок

Для середніх степеневих невід’ємних чисел справедливі твердження:

Різні способи дослідження нерівності Гельдера для просторів n-вимірних векторів

Простори n-вимірних векторів назвемо спряженими, якщо

Теорема 1 (Нерівність Гельдера для просторів n-вимірних векторів)

Для двох n-вимірних векторів з спряжених просторів справедлива нерівність Гельдера, тобто сума модулів добутків всіх відповідних координат векторів не перевищує добутку їх норм у відповідних просторах, в нерівності має місце знак рівності тоді і тільки тоді коли модулі всіх координат вектора в степені пропорційний відповідним модулям координат вектора в степені з невід’ємним коефіцієнтом пропорційності, тобто

а)

б)

Сума модулів добутків координат векторів х і у відповідно з простору і не перевищує добутку їх норм в цих просторах і в нерівності має місце знак рівності тоді і тільки тоді, коли модулі всіх координат вектора у рівні між собою і рівні нормі цього вектора в просторі .

Доведення

Для доведення нерівності Гельдера використовуємо критерії Ієнсена

Будемо вважати, що всі координати вектора не рівні 0:

Покладемо

Нехай хоча б одна з координат вектора у дорівнює 0, не обмежуючи загальності, можемо вважати, що , тобто