Достатні умови опуклості функції від багатьох змінних

О1. Похідною 1-го порядку функції від n-змінних в точці називається вектор-градієнт функції в цій точці, тобто вектор, всі координати якого дорівнюють частинним похідним першого порядку функції в цій точці.

Похідною 2-го порядку функції від n-змінних в точці, яка має всі частинні похідні диференційовані в цій точці, називають матрицею, кожен і-ий рядок якої складається з частинних похідних 2-го порядку по змінній x_i в цій точці, тобто

.

Теорема 1 (достатня умова строгої опуклості функції від n-змінних)

Нехай функція від n-змінних має всі частинні похідні 2-го порядку неперервна на опуклій відкритій множині. Якщо в кожній точці цієї множини матриця похідної 2-го порядку функції строго додатньо (від’ємно) визначена, то функція відповідно строго опукла донизу, догори, на цій множині, тобто

Доведемо І.

Доведення. Якщо функція диференційовна в точці, то ця точка є внутрішньою точкою області визначення функції.

Оскільки , то B – відкрита множина.

За критерієм 2 строгої опуклості функціонала на множині В достатньо довести

За наслідком 1, достатня умова опуклості на проміжку, потрібно довести:

.

Для спрощення записів доведення будемо проводити для функції 2-х змінних З (3), використовуючи теорему про похідну від складної функції двох змінних, і теорему про рівність мішаних похідних, маємо:

Якщо

З Твердження ІІ доводиться аналогічно.

Наслідок. (Достатня умова строгої опуклості функції від змінних).

Нехай функція від змінних має неперервні частинні похідні 2-го порядку на опуклій відкритій множині. Якщо в кожній точці цієї множини всі головні мінори матриці похідної 2-го порядку в цій точці додатньо (від’ємно) визначені, то функція строго опукла донизу (догори) на множині В.

Доведення.

Встановлення опуклості поверхонь другого порядку

Визначити тип поверхонь, накреслити малюнок та встановити їх опуклість на множині внутрішніх точок області визначення цих поверхонь.

П риклад 1.

1. Методом перерізів встановимо вид поверхні Якщо:

Отже ця поверхня є параболоїд обертання.

Використовуючи наслідок одержимо

П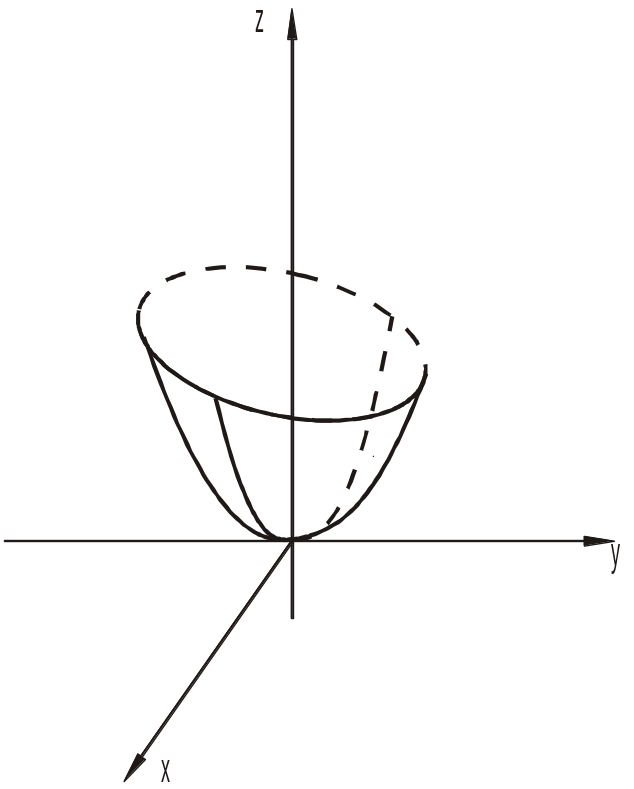 риклад 2.

Отже, поверхня є однопорожнинним еліптичним параболоїдом.

Використовуючи наслідок, маємо

Нерівність Юнга

Добуток n додатніх чисел менше рівне ніж сума цих чисел в додатніх степенях, поділених на ці степені, якщо сума всіх чисел, обернених до степенів, дорівнює 1 і в нерівності має місце знак рівності, тоді і тільки тоді, коли всі числа у відповідних степенях рівні між собою.

Доведення

Використаємо допоміжну функцію і достатню умову строгої опуклості функції донизу на проміжку маємо

З (1) (2), використовуючи критерій Ієнсена, маємо

Наслідок

Добуток двох додатніх чисел не перевищує суми цих чисел в додатніх степенях поділені на ці степені, якщо сума чисел обернених до степенів дорівнює 1. В нерівності має місце знак рівності тоді і тільки тоді, коли числа у відповідних степенях рівні

Доведення

;

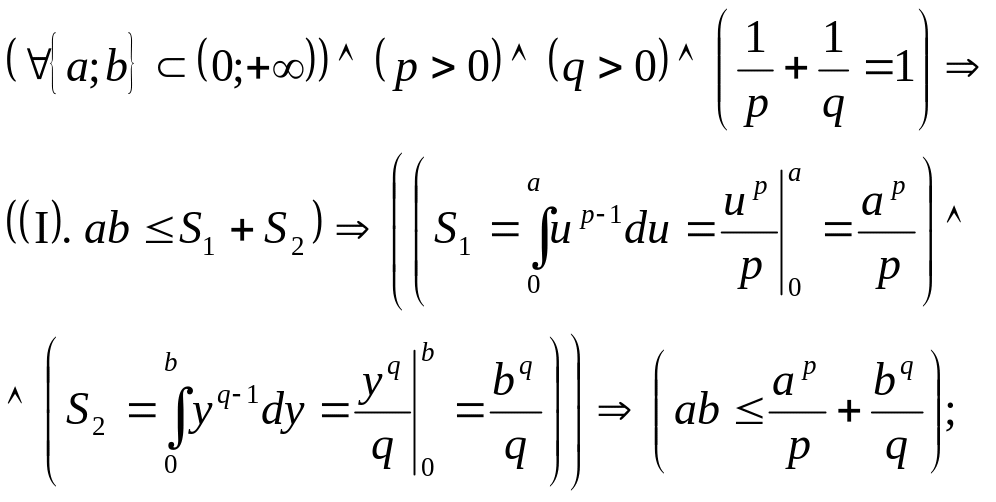
Зауваження: Нерівність Юнга справедлива і для невід’ємних чисел