
- •Властивості віддалі. Означення метричного простору і найкращого наближення елемента множини метричного простору.
- •Приклади метричного простору, елементами яких є довільні об’єкти.
- •Лінійні простори. Приклади
- •Лінійні нормовані простори. Приклади. Властивості норми.
- •3. Неперервність норми.
- •4. Властивість рівномірної неперервності функціонала норми.
- •Евклідові простори.
- •Означення і приклади евклідових просторів.
- •Опуклі множини
- •Критерії опуклості множини:
- •Опуклі функціонали
- •Достатні умови опуклості функції від однієї змінної.
- •Теорема 1 (достатня умова строгої опуклості функції від однієї змінної в точці).
- •Критерії знаковизначеності матриць
- •Теорема 1 (критерії Сильвестра знаковизначеності і невизначеності матриць)
- •Достатні умови опуклості функції від багатьох змінних
- •Теорема 1 (достатня умова строгої опуклості функції від n-змінних)
- •1. Методом перерізів встановимо вид поверхні Якщо:
- •Нескінченна диференційовність добутку функцій і складної функції
- •Нерівність між середніми
![]() Елементи
функціонального аналізу і теорії
наближення
функцій.
Елементи
функціонального аналізу і теорії
наближення
функцій.
Метричні простори.
Властивості віддалі. Означення метричного простору і найкращого наближення елемента множини метричного простору.
З шкільного курсу математики
відомо, що віддаль між двома точками
на прямій визначається так:
![]() ;
на площині:
;
на площині:
![]() і
і
в тривимірному просторі:
![]() .
.
З означення границі послідовності
![]() випливає, що в цьому означенні
фігурує поняття віддалі. Оскільки
означення границі використовується
при формулюванні багатьох понять
математики, то поняття віддалі відіграє
важливу роль в усіх розділах математики.
випливає, що в цьому означенні
фігурує поняття віддалі. Оскільки
означення границі використовується
при формулюванні багатьох понять
математики, то поняття віддалі відіграє
важливу роль в усіх розділах математики.
О1. Нехай
![]() .
Віддаллю між
елементами множини
.
Віддаллю між
елементами множини
![]() називається відображення
називається відображення
![]() ,
тобто дійсну функцію
,
тобто дійсну функцію
![]() від двох дійсних змінних, яка задовільняє
аксіоми Лінденбаума: І.
від двох дійсних змінних, яка задовільняє
аксіоми Лінденбаума: І.
![]() ;
ІІ.
;
ІІ.
![]() .
.
Властивості віддалі.
Теорема про невід’ємність і симетричність віддалі.
Віддаль між будь-якими двома елементами невід’ємна і симетрична, тобто:
а)
![]() ;
б)
;
б)
![]() .
.
Доведемо твердження б.
Покладемо
![]() .
Тоді, використовуючи аксіоми Лінденбаума,
маємо:
.
Тоді, використовуючи аксіоми Лінденбаума,
маємо:
![]() (1).
(1).
Якщо
![]() замінити на
замінити на
![]() то аксіому І можна записати так:
то аксіому І можна записати так:
![]() (2).
(2).
Покладемо
![]() .
Тоді з нерівності (2), використовуючи
аксіоми Лінденбаума, одержимо:
.
Тоді з нерівності (2), використовуючи
аксіоми Лінденбаума, одержимо:
![]() (3).
(3).
З (3) і (1) випливає, що
![]() .
.
Доведемо твердження а.
Покладемо
![]() .
Тоді, використовуючи аксіоми Лінденбаума,
маємо:
.
Тоді, використовуючи аксіоми Лінденбаума,
маємо:
![]() .
.
Теорему доведено.
О2. Метричним простором
називають непорожню
множину, для елементів якої введено
поняття віддаль і позначають
![]() .
.
Термін метричний простір ввів французький математик Фреше 1919 р., а «три» аксіоми простору — німецький математик Хаусдорф.
З аксіоми I
Лінденбаума і симетричності віддалі
випливає нерівність трикутника
![]() .
Доведемо узагальнену нерівність
трикутника.
.
Доведемо узагальнену нерівність
трикутника.
![]() .
.
Доведення проведемо методом математичної індукції.
1. Перевіримо істиність
нерівності при
![]() ,
тобто
,
тобто
![]() .
.
![]() .
Остання нерівність є нерівністю
трикутника.
.
Остання нерівність є нерівністю
трикутника.
2. Припустимо, що нерівність
істина при
![]() ,
тобто
,
тобто
![]() .
.
3. Доведемо, використовуючи
припущення і нерівність трикутника, що
нерівність істина при
![]() ,
тобто
,
тобто
![]()
Використовуючи нерівність
трикутника і припущення, маємо:
![]() .
Позначимо через
.
Позначимо через
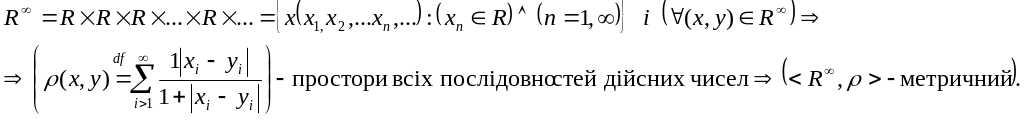
Доведемо, що
![]() простір.
простір.
Перевіримо виконання аксіоми II.

З (1) за означенням рівності
послідовностей випливає, що
![]() .
Отже виконується аксіома ІІ Лінденбаума.
.
Отже виконується аксіома ІІ Лінденбаума.
Перевіримо виконання аксіоми І. Доведемо нерівність
![]() (І)
(І)
I спосіб. Нехай
![]() , де
, де
![]() .
Тоді
.
Тоді
![]() Тому, згідно з достатньою
умовою монотонності функції, функція
Тому, згідно з достатньою
умовою монотонності функції, функція
![]() строго зростаюча на проміжку
строго зростаюча на проміжку
![]() .
Використовуючи монотонність функції
і властивості модулів, одержимо:
.
Використовуючи монотонність функції
і властивості модулів, одержимо:
![]()
Нерівність І доведена.
ІІ спосіб. Нерівність (І)
рівносильна нерівності
![]()
Використовуючи нерівність I одержимо:
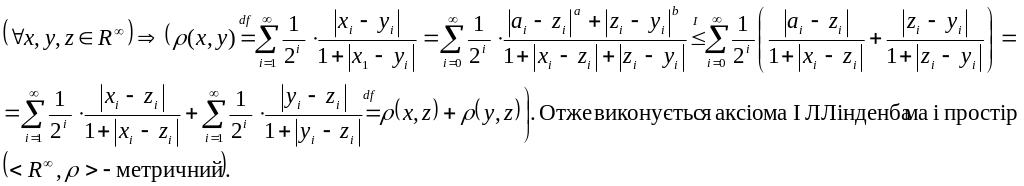
Основні задачі теорії наближень зводяться
до знаходження віддалі від елемента x
до множини F
метричного простору, тобто до знаходження
величини
![]() ,
яку називають найкращим
наближенням елемента
x множиною
F і
позначають
,
яку називають найкращим
наближенням елемента
x множиною
F і
позначають
![]() і до знаходження віддалі між двома
множинами
і до знаходження віддалі між двома
множинами
![]() ,
яку називають найкращим наближенням
множини М
множиною F і
позначають
,
яку називають найкращим наближенням
множини М
множиною F і
позначають![]() .
.
Приклади метричного простору, елементами яких є довільні об’єкти.
Нехай
![]() Доведемо, що простір
,
який називають простором ізольованих
точок, метричний. Перевіримо виконання
аксіоми І Лінденбаума, тобто
Доведемо, що простір
,
який називають простором ізольованих
точок, метричний. Перевіримо виконання
аксіоми І Лінденбаума, тобто
![]() Використовуючи означення віддалі в
просторі ізольованих точок, маємо:
Використовуючи означення віддалі в
просторі ізольованих точок, маємо:
а)
![]()
б)
![]() .
.
в)
![]() .
Інших випадків для елементів
.
Інших випадків для елементів
![]() множини
бути
не може. Отже аксіома І Лінденбаума
виконується.
множини
бути
не може. Отже аксіома І Лінденбаума
виконується.
Використовуючи означення віддалі в просторі ізольованих точок, одержимо:
![]() .
Отже виконується аксіома ІІ Лінденбаума,
і простір ізольованих точок метричний.
.
Отже виконується аксіома ІІ Лінденбаума,
і простір ізольованих точок метричний.
Нехай простір
![]() - метричний і
- метричний і
![]() .
Доведемо, що простір
.
Доведемо, що простір
![]() - метричний.
- метричний.
Перевіримо виконання аксіоми I Лінденбаума. Використовуючи нерівність I і аксіому Лінденбаума для простору , одержимо:
![]() .
Отже виконується аксіома І Лінденбаума.
Використовуючи означення віддалі в
просторі
і аксіому ІІ Лінденбаума, маємо:
.
Отже виконується аксіома І Лінденбаума.
Використовуючи означення віддалі в
просторі
і аксіому ІІ Лінденбаума, маємо:
![]() .
Отже виконується аксіома ІІ Лінденбаума,
і простір
- метричний.
.
Отже виконується аксіома ІІ Лінденбаума,
і простір
- метричний.
