2. Теорема о непрерывности дифференцируемой функции.

Если ф-ция f(x) дифф. в точке x₀, то она и непрерывна в этой точке.

lim_Δx→0Δf/Δx=f ^|(x₀)

Δf=f(x)- f(x₀)=f(x₀+Δx)-f(x₀)

(f(x₀+Δx)-f(x₀))/(Δx) - f ^|(x₀) – БМВ(Δx→0)

(f(x₀+Δx)-f(x₀))/(Δx) - f ^|(x₀)=α(x)

f(x₀+Δx)-f(x₀)=f ^|(x₀)Δx+α(x)Δx

Δf ^|| - БМВ

Ф-ция f непрерывна в точке x₀

3. Правила дифференцирования.

1) f(x)=const, то f ^|(x)=0

2) [C(f(x))]^|=C*f ^|(x)

C(f(x))=g(x)

lim_x→0(Δg/Δx)=lim_x→0(Cf(x)-Cf(x₀))/(x-x₀)= Clim_x→0(f(x)-f(x₀))/(x-x₀)=Cf ^|(x₀)

3. Производная алгебраической суммы равна алгебраической сумме производных. .

Покажем это. Пусть некоторая функция у, равная имеет приращение . Тогда функции и тоже должны получить приращения и , соответственно. Новое значение будет , а для – , следовательно,

Найдем по определению (2) производной

.

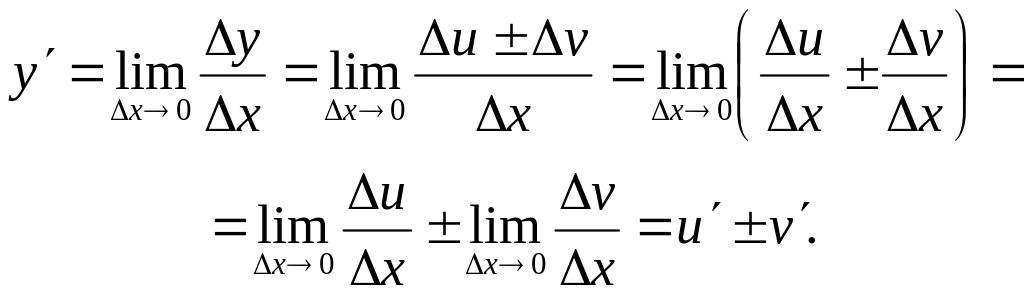4. Производная произведения равна . Покажем спра­вед­ли­вость этого равенства.

Если, как в первом случае, дать приращение , то функции u и v также получат приращение, следовательно, и функция тоже изменится. Найдем .

.

По определению производной

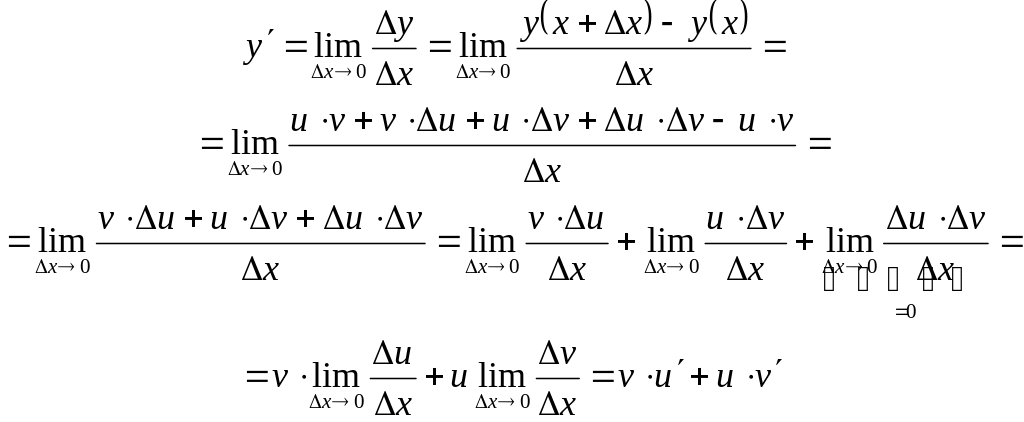
Если необходимо вычислить производную нескольких сомножителей, например, , если все три функции имеют производные в точке , используя правило вычисления производной для двух сомножителей, получим

5. Производная частного. Рассмотрим функцию , причем, кроме су­щес­твования производных в точке для функций и необходимо по­ло­жить, что в точке отлична от нуля.

Найдем .

и тогда из определения производной имеем

.

4. Производная сложной функции.

Для того чтобы функция была дифф в точке x₀, необходимо и достаточно, чтобы ее приращение Δf было представлено в виде:

Δf=AΔx+БМВ, А – const

неопределенность:

f(x) x₀ f ^|(x₀)

lim_Δx→0(Δf/Δx)=f ^|(x₀)

(Δf/Δx)- f ^|(x₀)=БМВ

Δf= f ^|(x₀)Δx+БМВΔx

Достаточность:

Δf=AΔx+БМВ | :Δx

Δf/Δx=А+БМВ/Δx

БМВ/Δx→0

БМВ должна быть более высокого порядка чем Δx.

Теорема о производной сложной функции

y(x) x₀ y ^|(x₀)=y^|₀

z(x) y₀ z ^|(y₀)= z^|₀

y₀=y(x₀)

z(y(x))= (x₀)

(x₀)=z ^|_y(y₀) y ^|_x(x₀)= z ^|₀ y ^|₀

Δ = (x₀+Δx)- (x₀)=z(y(x₀+Δx))-z(y(x₀))= z(y₀+Δy)-z(y₀)=Δz=z^|(y₀)Δy+α= z^|(y₀)[y^|₀(x₀)Δx+β]+α= z^|(y₀)y^|₀(x₀)Δx+z^|(y₀)β+α; z^|(y₀)β+α – БМВ

• (x₀)= z ^|(y₀) y ^|(x₀)= z ^|₀ y ^|₀

4. Производная сложной функции. Пусть дана , где . Тогда имеет место теорема, которую приведем здесь без доказательства.

Теорема. Если функция имеет в точке производную и функция имеет в точке производную , тогда сложная функция имеет в точке производную, равную

5. Производная обратной функции.

y=y(x) дифф. в точке x₀ y₀=y(x₀) y^|(x₀)≠0

x=x(y) -> обратная ф-ция y, тогда в точке у₀ функция х дифференцируема и ее производная х^|(y₀)=1/y^|(x₀)

х^|(y₀)=lim_Δy→0(Δx/Δy)=lim_Δy→0(1/(Δy/Δx))= lim_Δx→0(1/(Δy/Δx))= 1/y^|(x₀)

6. Производная обратной функции.

Теорема. Если имеет в точке производную, отличную от нуля, тогда в этой точке обратная функция также имеет производную и имеет место соотношение

. (6)

Пользуясь этой теоремой, найдем производные обратных три­го­но­мет­ри­чес­ких функций.

1. на интервале . , тогда , от­ку­да сле­до­ва­тель­но, .

2. . . , откуда

3. . ; , откуда

4. ; ;

5. , где и являются функциями от . Для нахождения применим формулу (5). Для этого предварительно найдем функцию

и ее производную

.

По формуле (5) получаем .

Эту же формулу можно получить иначе. Представим в виде

и найдем производную этой функции

.