
- •1. Множества и операции над ними.
- •2. Отображения
- •3.Топологические структуры. Классификация точек множества.
- •5.Модуль и его свойства.
- •Модуль и основные неравенства.
- •1. Предел числовой последовательности.
- •2.Основные теоремы о пределах
- •3. Бмв. Теоремы о бмв
- •4. Свойства пределов выражаемые равенствами.
- •5. Свойства пределов выражаемые неравенствами
- •6.Принцип вложения отрезков. Теорема о «2х милиционерах»
- •7. Определение предела функции
- •8. Односторонние пределы функции
- •§9. Односторонние пределы. Необходимое и достаточное
- •9. Замечательные пределы
- •10. Классификация бмв. Эквиваленты.
- •11. Непрерывность функции. Теорема о приращении непрерывной функции.
- •12.Свойства непрерывных функций.
- •13. Непрерывность суперпозиции функции.
- •14. Теоремы Больцмана-Коши
- •15. Теорема Вейерштрасса
- •16. Классификация разрывов.
- •1. Производная, ее механический и геометрический смысл.
- •2. Теорема о непрерывности дифференцируемой функции.
- •3. Правила дифференцирования.
- •4. Производная сложной функции.
- •5. Производная обратной функции.
- •6. Производная элементарных функций.
- •7. Дифференциал функции. Свойства и геометрический смысл.
- •8.Инвариантность(неизменность) формы первого дифференциала.
- •9. Производные функции, заданных параметрически и неявно.
- •10. Производные и дифференциалы высших порядков.
- •11. Теоремы Ферма, Ролля, Коши и Лагранжа.
- •12. Признаки возрастания и убывания функции.
- •13. Экстремум функции. Достаточные условия.
- •14. Выпуклость функции, точки перегиба. Достаточные условия.
- •15. Асимптоты, их нахождение.
- •16. Теоремы Лопиталя.
- •17. Формула Тейлора с остаточным членов в форме Лагранжа и Пеано.
5.Модуль и его свойства.
Модуль вещественного числа x есть расстояние от x до нуля.
Более точно: Модуль x есть неотрицательное число, обозначаемое |x|, определяемое следующим образом: если x ≥ 0, то |x|=x; если x < 0, то |x| = −x. Для абсолютной величины имеют место следующие соотношения:
|a| ≥ 0
|a| = 0 тогда и только тогда, когда a = 0.
|ab| = |a||b|
Модуль действ. числа и его свойства.

Модуль и основные неравенства.
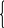 x;
x>0
x;
x>0
х= 0; x=0
-x; x<0

|x|<h -h<x<h |x|>h x>h
h>0 x<-h
а,b R: |ab|a|+|b|
а,b R: |a-b|||a|-|b||
Можно рассматривать окрестности бесконечности:
О ε(+)={xR:x>ε}
(//////////
x
ε(+)={xR:x>ε}
(//////////
x
ε>0 ε
О ε(-)={xR:x<-ε}
///////////)
x
ε(-)={xR:x<-ε}
///////////)
x
ε>0 -ε 0
О ε()={xR:x>ε}
\\\\\\)
(////// x
ε()={xR:x>ε}
\\\\\\)
(////// x
x>ε;x<-ε -ε ε
1. Предел числовой последовательности.
если каждому натуральному n поставлено число хn, то говорят что задана числовая последовательность х1,x2…xn={xn}
O:Числ. посл. называется занумерованная совокупность чисел рассматриваемая в порядке возрастания. Общий эл-т последовательности является функцией от n. xn=f(n)
O: Последовательность {xn} – ограниченная, если существует M>0, что для любого n верно: |хn|<M, т.е. все члены последовательности принадлежат промежутку (-M;M)
O: Последовательность {xn} – ограниченная сверху, если для любого n сущ. M такое, что xn≤M
O: Последовательность {xn} – ограниченная снизу, если для любого n сущ. M такое, что xn≥M
O: Число а называется пределом последовательности {xn}, если для любого положительного ξ>0 сущ. такой номер N, что для всех n>N выполняется: |a-xn|<ξ (запись limxn=a), в таком случае говорят, что {xn} сходится к а при n→∞
C: если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом, если сходится она из них, то сходится и другая.
O: число а назыв. пределом послед. {xn}, если в ξ окрестности содержится только конечное число членов числ. послед.

2.Основные теоремы о пределах
1) последовательность не может иметь более одного предела. док-во:
предположим что посл. имеет 2 предела a и b, a≠b. Тогда по опред. существ. ξ>0, что |a-xn|<ξ/2, |b-xn|<ξ. Запишем |a-b|=|(a-xn)+(xn-b)|≤|a-xn|+|xn-b|<ξ/2+ξ/2=ξ, т.к. ξ-любое число, то |a-b|=0, т.е. a=b
2) теорема о пределе модуля: если xn→a, то |xn|→|a|. Док-во:
из xn→a след, что |xn-a|<ξ. В то же время ||xn|-|а||≤|xn-a|, т.е. ||xn|-|а||<ξ, т.е. |xn|→|a|
3) Если xn→а, то послед. {xn} ограничена.
Монотонная последовательность:
O: 1. если xn+1>xn для всех n, то последовательностьвозрастающ. 2. если xn+1≥ xn, для всех n, то послед. не убывающая. 3. если xn+1<n, то последовательность убывающая 4. если xn+1≤ xn, то послед. невосрастающая
Т: монотонная огранич. посл. имеет предел. док-во:
монотонная ограниченная посл. – посл. огранич. сверху xn≤M, М – некоторое число.
т.к. любое ограниченное сверху множ-во имеет четкую верхнюю грань, то для любого ξ>0 сущ. такое xn>a-ξ -> a-ξ<xn<a+ξ
-ξ<xn-a<ξ или |xn-a|<ξ, т.е. limxn=a
4) О разности. Для того чтобы число А было пределом числ. посл. {аn} необходимо и достаточно чтобы разность между посл. |аn-А|→0. Необходимость! сущ. {аn}=A это означ, что для любого ξ>0 сущ. Nξ, такое что n>Nξ и выполняется: |аn-А|<ξ <-> bn=аn-А <-> |bn|<ξ <-> |bn-0|<ξ
Достаточность! аn-А→0, любое ξ>0 сущ. Nξ n>Nξ

