- •Логинов а.С. Часть 1. Дифференциальное исчисление Глава 1. Ведение
- •1.1. Некоторые понятия теории множеств и математической логики
- •1.1.1. Множество, операции над множествами, обозначения
- •1.1.2. Отображение, взаимно-однозначное соответствие, счетное и несчетное множества
- •1.1.3.Некоторые понятия математической логики (Дж. Маллас Пролог)
- •1.1.4.Вещественные числа
- •1.2. Комплексные числа
- •1.2.1. Определение комплексного числа
- •1.2.2. Свойства комплексных чисел
- •1.2.3. Алгебраическая форма записи
- •1.2.4. Модуль и аргумент комплексного числа. Комплексное сопряжение. Тригонометрическая форма записи комплексных чисел
- •1.2.5. Формула Муавра
- •1.3. Верхняя и нижняя грани множества действительных чисел
- •1.3.1.Ограниченное множество. Точные грани
- •1.3.2.Существование точной верхней грани у ограниченного сверху множества
- •Глава 2. Последовательности
- •2.1. Основные понятия, относящиеся к последовательностям
- •2.1.1. Ограниченная последовательность. Точная верхняя (нижняя) грань. Монотонные последовательности
- •2.1.2. Предел последовательности
- •2.1.3. Несобственные пределы
- •2.2. Теоремы о пределах последовательностей
- •2.2.1.Простейшие свойства сходящихся последовательностей
- •2.2.2. Монотонные последовательности
- •2.3. Некоторые свойства последовательностей, связанные со свойством непрерывности вещественных чисел
- •2.3.1.Подпоследовательность. Теорема Больцано-Вейерштрасса
- •2.3.2.Верхний и нижний пределы последовательности
- •2.3.3. Фундаментальная последовательность. Критерий Коши для последовательности
- •2.4. Свойства последовательностей
- •2.4.1.Операции над последовательностями. Свойства пределов, связанные с операциями
- •Глава 3. Предел функции. Непрерывность
- •3.1. Основные понятия, относящиеся к функции
- •3.1.2.Ограниченность. Точные грани
- •3.1.3.Элементарные функции
- •3.2. Предел функции
- •3.2.2. Односторонние пределы. Предел слева, предел справа
- •3.2.3. Связь предела с односторонними пределами
- •3.2.5. Критерий Коши существования конечного предела функции
- •3.2.6. Локальная ограниченность функции, имеющей конечный предел
- •3.2.7. Сохранение знака функции, имеющей ненулевой предел в точке
- •3.2.8. Предел сложной функции
- •3.3 Свойства пределов
- •3.3.1. Переход к пределу в неравенствах
- •3.3.2. Арифметические операции над пределами
- •3.3.3. Бесконечно малые и бесконечно большие функции
- •3.3.4. Сравнение б.М. И б.Б. Функций. Символы o,o
- •3.4 Замечательные пределы Замечательные пределы, основные эквивалентности.
- •3.4.1. Первый замечательный предел.
- •3.4.2. Второй замечательный предел.
- •3.5 Непрерывные функции
- •3.5.2.Простейшие свойства непрерывных функций
- •Определение. Если существуют конечные пределы
- •3.5.3. Ограниченность непрерывной функции. Теоремы Вейерштрасса
- •3.5.4.Теорема о промежуточных значениях непрерывной функции
- •3.5.5.Критерий непрерывности монотонной функции
- •3.5.6.Непрерывность обратной функции
- •3.5.7.Непрерывность элементарных функций
- •3.5.8.Равномерная непрерывность
- •Глава 4 Дифференциальное исчисление
- •4.1 Производная
- •4.1.1.Определение производной. Геометрическая интерпретация. Необходимое условие дифференцируемости
- •4.1.2. Дифференциал функции
- •4.1.3.Основные правила дифференцирования
- •4.1.4.Производные элементарных функций
- •4.1.5. Логарифмическое дифференцирование
- •4.1.6.Функции, заданные параметрически
- •4.2 Производные и дифференциалы высших порядков
- •4.2.1.Производные высших порядков
- •4.2.2. Вычисление производных функций, заданных неявно
- •4.2.3. Формула Лейбница
- •4.2.4. Дифференциалы высших порядков
- •4.2.5. Инвариантность формы дифференциала первого порядка
- •4.2.6. Дифференцирование функций, заданных неявно
- •4.3 Теоремы о среднем для дифференцируемых функций
- •4.3.1. Теорема Ферма о нуле производной
- •4.3.2. Теорема Ролля о нуле производной
- •4.3.3. Теорема Лагранжа о конечных приращениях
- •4.3.4. Теорема Коши о конечных приращениях
- •4.4 Правило Лопиталя
- •4.4.1.Раскрытие неопределенностей вида 0/0
- •4.4.2.Раскрытие неопределенностей вида /
- •4.4.3.Использование правила Лопиталя для выделения главных частей и определения порядков бесконечно больших
- •4.4.4.Раскрытие неопределенностей вида 0, 1 , 00, 0, -
- •4.5 Формула Тейлора
- •4.5.1.Многочлен Тейлора. Формула Тейлора с остаточным членом Rn
- •4.5.2. Остаток в форме Пеано
- •Лемма. Если
- •4.5.3.Другие формы остатка в формуле Тейлора
- •4.5.4. Разложение некоторых элементарных функций по формуле Тейлора
- •4.5.5. Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов
- •4.5.6. Формула Тейлора для четных и нечетных функций
- •4.6 Исследования характера поведения функций
- •4.6.1.Условие монотонности функции
- •4.6.2.Максимальные и минимальные значения функций ( экстремумы )
- •Аналогично определяются: минимум, строгий минимум.
- •4.6.3. Исследование функций на экстремум по знаку высших производных
- •4.6.4. Выпуклость функции, точки перегиба
- •4.6.5. Асимптоты функций
- •4.6.6. Общая схема построения графиков
- •Глава 5. Элементы теории кривых
- •5.1 Векторная функция скалярного аргумента
- •5.1.1.Определение векторной функции. Операции над векторными функциями
- •5.1.2. Предел вектор функции
- •5.1.3. Непрерывность вектор функции
- •5.1.4. Дифференцируемость вектор функции
- •5.1.5. Правила дифференцирования вектор функций
- •5.1.6. Гладкие кривые Определение. Кривая
- •5.2 Длина кривой
- •5.2.1.Спрямляемая кривая
- •5.3 Плоские кривые
- •5.3.1.Понятие кривизны и ее вычисление
- •5.3.2.Выражение центра и радиуса кривизны для явно заданной кривой
- •5.3.3.Порядок соприкосновения кривых
4.6.6. Общая схема построения графиков
Можно рекомендовать следующую последовательность исследования поведения функции.
1 Область определения. Симметрия ( четность, нечетность ). Периодичность.
2 Асимптоты
3 Интервалы монотонности, экстремумы ( заполняется таблица, как показано ниже )
4 Дополнительные исследования ( если необходимо, выпуклость, точки перегиба, пересечение с осями и т. п. )
Замечание. Отыскание глобальных максимумов и минимумов на отрезке производится среди точек трех типов:
стационарные точки
особые точки (где не существует производная)
граничные точки.
Пример.
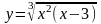 Асимптоты
y/x1,
x
Асимптоты
y/x1,
x
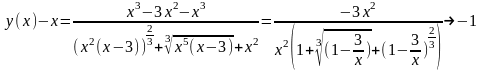 при
x
.
при
x
.
Асимптота y=x-1
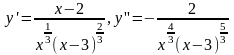
Особые точки ( в первом приближении только для первой производной ) 0,2,3
-
t
(-,-1)
-1
(-1,1)
1
(1,)

+
+
-
x
- -3
-3
-3 1
1
1 -
Диапазон x
(-,-3)
(-3,1)
(-,1)
dy/dx
-
0
+
3
+
y(x)
-2
-2
-22
2
-2
d2y/dx2
+
+
-
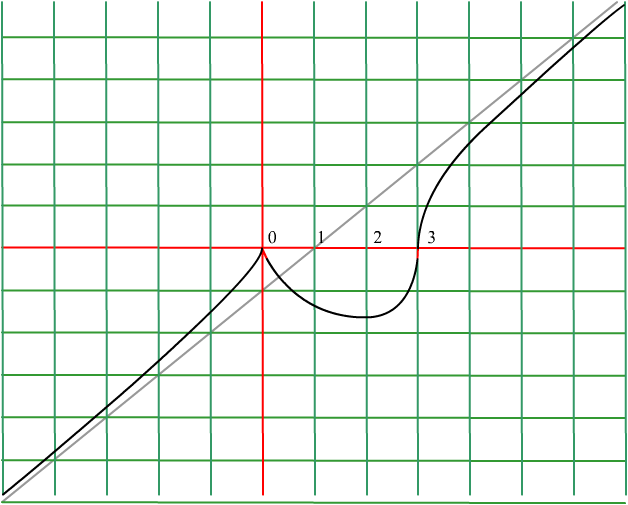
Рис. 4.23
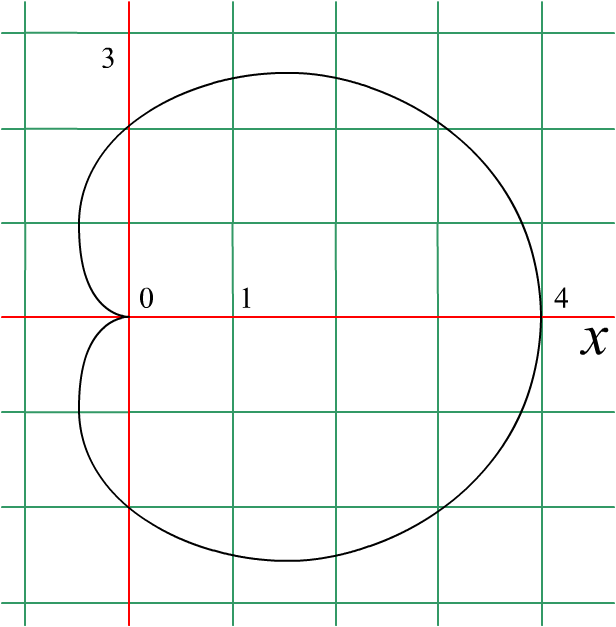
Пример. Исследовать поведение кардиоиды r = 2(1 + cos t) в окрестности точек t = 0, t = .
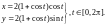
 =
=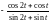 .
.
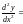
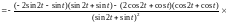
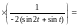

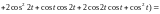
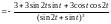 =
=
Для
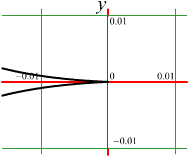
нахождения точек перегиба полезно
методом сложения графиков построить
приблизительно график функции
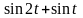 .
Из этого графика видно, что направление
выпуклости меняется в районе точек
.
Из этого графика видно, что направление
выпуклости меняется в районе точек
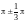 и точки
и точки
 (из
за знаменателя). Около точки
числитель
не меняет знак, а знаменатель меняет,
так образом, это тоже точка перегиба.
(из
за знаменателя). Около точки
числитель
не меняет знак, а знаменатель меняет,
так образом, это тоже точка перегиба.
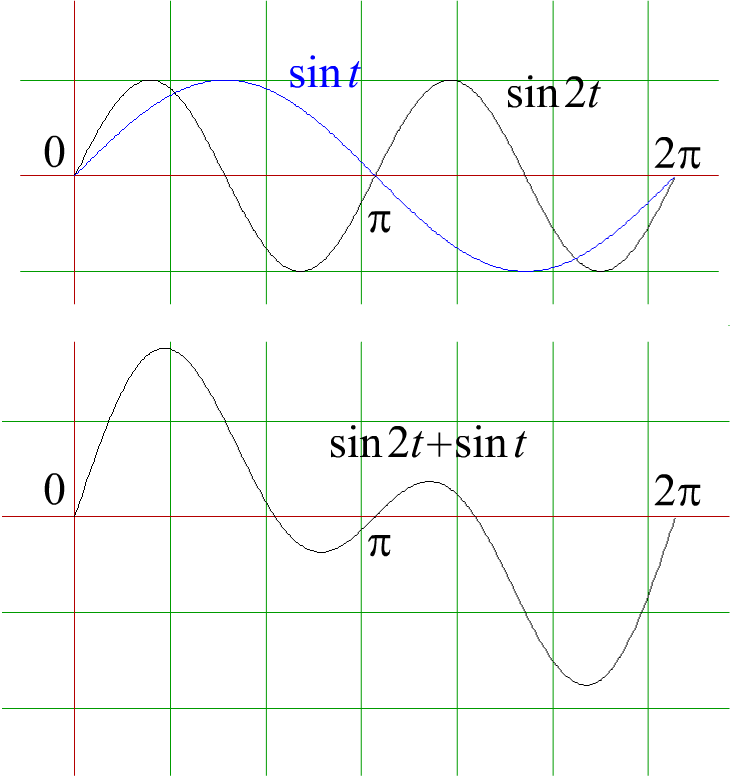
Рис. 4.24
|
|
|
|
Рис. 4.25
Глава 5. Элементы теории кривых
5.1 Векторная функция скалярного аргумента
Кривые на поскости и в пространстве. Векторная функция.
5.1.1.Определение векторной функции. Операции над векторными функциями
На плоскости
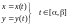 ,
r(t)=x(t)i+y(t)j
.
,
r(t)=x(t)i+y(t)j
.
В пространстве
 ,
r(t)=x(t)i+y(t)j
+y(t)k
.
,
r(t)=x(t)i+y(t)j
+y(t)k
.
Операции над вектор функциями
1) p(t), q(t) p(t)+ q(t).
2) (t)r(t).
3) Скалярное произведение (p(t) , q(t)).
4) В трехмерном пространстве определено векторное произведение [ p(t) , q(t) ].
5.1.2. Предел вектор функции
Определение
r(t)=a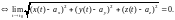
Или, что тоже, |r(t) – a|=0 .
Замечание 1. Это определение не зависит от выбора базиса i , j , k.
Геометрическая интерпретация.
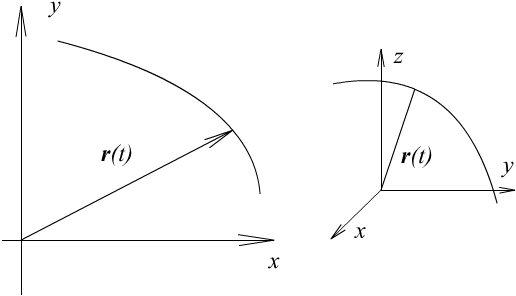
Рис. 4.26
Теорема. (Критерий существования предела вектор функции) Для существования предела
r(t) = a необходимо и достаточно существования пределов координат вектор функции
r(t)
= a
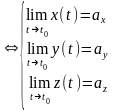
Доказательство. Для заданного значения параметра t обозначим
(t) = max{|x(t)-ax|,| y(t)-ay |,| z(t)-az |}. Для любого t справедливо неравенство
(t)
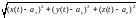 =|r(t)
– a|.
=|r(t)
– a|.
С другой стороны |r(t)–a|=
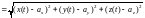
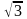 (t).
(t).
Из этих неравенств и следует требуемое утверждение.
Замечание 2. Для существования предела необходимо требовать, чтобы r(t) была определена в некоторой проколотой окрестности точки t0. Можно рассматривать односторонние производные.
Из теорем о пределах функций, с помощью доказанного критерия, получаются соответствующие теоремы для пределов вектор функций. Перечислим некоторые из них.
Предел, если он существует, единственен.
Предел суммы и произведения на обычную функцию
( p(t)+q(t) )= p(t)+ q(t).
((t) p(t))= (t) p(t).
3) (p(t) , q(t))=(a , b).
a= p(t) , b = q(t) .
Доказательство.
Пусть p(t)=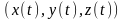 ,q(t)=
,q(t)=
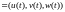 ,
a=
,
a=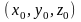 ,
b
=
,
b
=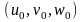 . Тогда
(
p(t),q(t))=
. Тогда
(
p(t),q(t))=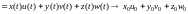 =
(
a
, b
).
=
(
a
, b
).
4) [ p(t) , q(t)]=[ a , b ] , если a= p(t) , b = q(t) .
Для краткости введем обозначения:
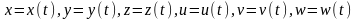 .
.
[p(t),q(t)]=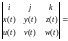
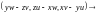
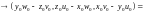
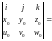 [
a
, b
].
[
a
, b
].