4.6.4. Выпуклость функции, точки перегиба

Хорда, соединяющая точки M₁(x₁, f(x₁)), M₂(x₂, f(x₂)) графика функции f(x) задается функцией

y=L(x, x₁, x₂ ) = + (*)

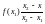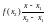Это проверяется подстановкой координат x₁, x₂ в правую часть (*).

Определение. Функция f(x) называется выпуклой вверх на [a,b], если для x₁<x<x₂ из [a,b]

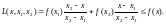(1)

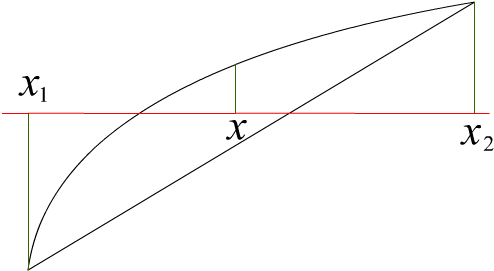
Рис. 4.18

Аналогично определяется выпуклая вниз функция. Можно дать определение строгой выпуклости, заменив нестрогое неравенство на строгое в (1) .

Теорема ( Достаточное условие выпуклости )

Если f непрерывна на [a,b], дважды дифференцируема на (a,b) и f(x)>0 на (a,b), то f строго выпукла вниз.

Доказательство. Для любых 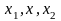, ax₁<x<x₂b имеем

=

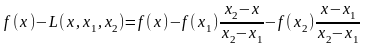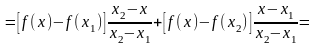
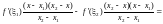
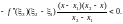
Участвующие в этих соотношениях величины расположены на оси в показанном на рисунке порядке.

Рис. 4.19

Определение. Точка x₀ называется точкой перегиба функции f, если в точке x₀ существует касательная и в некоторой окрестности точки x₀ график f лежит по разные стороны от касательной.

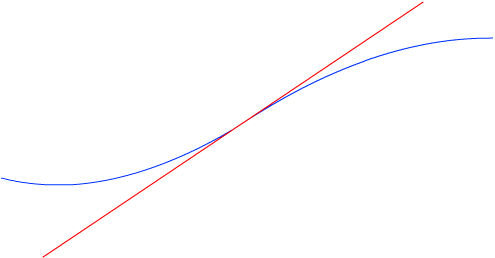
Рис. 4.20

Теорема 1. ( Необходимое условие точки перегиба )

Если f дважды непрерывно-дифференцируема в окрестности точки перегиба x₀, то f(x₀)=0.

Доказательство. Противное f(x₀)  0. По теореме о сохранении знака f(x) сохраняет знак в окрестности точки x₀ . По формуле Тейлора с остатком Лагранжа

Левая часть этого равенства имеет смысл уклонения точки графика функции от касательной. Это, в свою очередь, означает, что график функции лежит с одной стороны от касательной.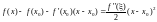 не меняет знак.

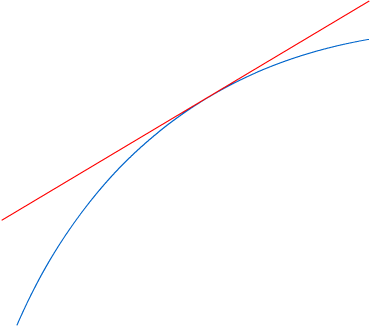
Рис. 4.21

Теорема 2 ( Достаточное условие точки перегиба )

1. f(x) в U(x₀) и f(x₀)=0

2. f меняет знак при переходе через точку x₀ .

Тогда x₀ точка перегиба.

Доказательство. По формуле Тейлора с остатком Лагранжа

.

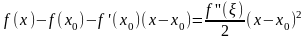Следствие. Если f(x₀)=0 и f(x₀) 0, то x₀ – точка перегиба.

Доказательство. При данных условиях f будет монотонной, и будет менять знак при переходе через x₀ .

4.6.5. Асимптоты функций

Определение. Пусть f определна на полуоси x>c. Прямая y=ax+b называется наклонной асимптотой при x+ , если .

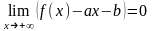Пусть f определна на полуоси x < c . Прямая y=ax+b называется наклонной асимптотой при x-, если .

Пример.

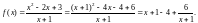
В дальнейшем рассматривается лишь случай +.

Теорема. Пусть f(x) определена на [c,+ ). Для того, чтобы прямая y=ax+b была асимптотой функции f необходимо и достаточно, чтобы

1)

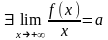
2)

Пример.

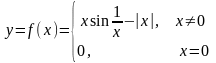
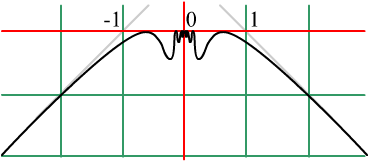
Рис. 4.22

Наклонные асимптоты: в + линия y= - x+1, в - линия y = x+1.

Вертикальная асимптота

Функция f определена на (a,a+). Линия x=a называется вертикальной асимптотой, если 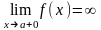, аналогично при xa - 0.

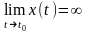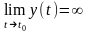Для нахождения наклонных асимптот параметрически заданных функций поступают похожим образом. Вначале разыскиваются значения параметра t₀ , для которых и . Далее коэффициенты наклонной асимптоты находятся из соотношений

1)

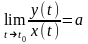
2) 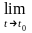(y(t) – a x(t)) = b ,

при условии, что указанные пределы существуют.

Для нахождения вертикальной асимптоты вида x=x₀ параметрически заданных функций находят t₀ такие, что 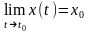, . Для горизонтальной асимптоты ,