3.5.6.Непрерывность обратной функции

Еще раз определение обратной функции. Пусть f(x) определена на X и Y – множество ее значений. Предположим, что различным значениям x₁ и x₂ соответствуют различные значения y₁ =f(x₁), y₂=f(x₂). Тогда для любого y Y !xX: y=f(x), такое соответствие y x называется обратной функцией и обозначается x=f ^-1(y). У обратной функции областью определения будет Y , а областью значений X.

Лемма. Обратная функция строго монотонно возрастающей функции будет строго монотонно возрастать. Обратная функция строго монотонно убывающей функции будет строго монотонно убывать.

Доказательство. Например, пусть f(x) строго монотонно возрастает. Если y₁ ,y₂ из области значений функции f(x) и y₁ < y₂ , то

f ^-1(y₁) < f ^-1(y₂). Действительно, если предположить противное: 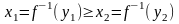, то из условия монотонного возрастания функции f(x) получим неравенство y₁= f(x₁)  f (x₂)=y₂ , что противоречит условию y₁ < y₂ . Аналогично доказывается, что обратная к монотонно убывающей функции является монотонно убывающей функцией.

Теорема ( существование и непрерывность обратной функции у монотонной )

Если y=f(x) строго монотонно возрастает на [a,b] и непрерывна там, то на Y=[f(a),f(b)] существует обратная функция и является непрерывной на этом множестве.

Доказательство. Существование обратной функции следует из строгой монотонности. Кроме того, обратная функция также будет монотонной с областью значений [a,b]. Из критерия непрерывности монотонной функции следует ее непрерывность. Аналогичная теорема имеет место для строго монотонно убывающей функции.

3.5.7.Непрерывность элементарных функций

1) Непрерывность функции a^x, a>0.

Справедливо равенство .

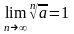a) Если a>1, обозначим 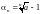, a=(_n+1)ⁿ > n_n, _n<a/n , следовательно _n – б.м..

Замечание. Отметим, что точно также можно доказать равенств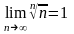о . Именно, 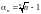, n=(_n+1)ⁿ > ,

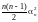_n<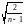 , следовательно _n – б.м..

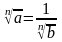b) Если a <1, то , b > 1.

Докажем, что (непрерывность в 0 функции a^x ).

1 a> 1.

Докажем вначале, что 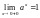. Пусть {x_k} последовательность типа Гейне для , то есть, x_k0, x_k>0. Можно считать, что . Для последовательности целых частей 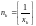будут выполнены неравенства 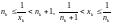. Откуда, в частности, следует, что n_k+ и 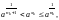далее, переходя к пределу при k , получим требуемое равенство (определение одностороннего предела по Гейне). Аналогично рассматривается случай x 0 - 0. Из существования и равенства односторонних пределов следует доказываемое утверждение: .

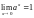2 Если a<1, то b^x=1/a^x,где b=1/a > 1.

2) Функция a^x непрерывна в точке x_{0 .} Это следует из равенства .

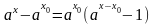3). Функция y=log_ax непрерывна, как обратная к непрерывной строго монотонной функции x=a^y .

4). Степенная функция y=x^. Докажем непрерывность при x>0. Имеем x^=e^{ ln x}, далее следует воспользоваться теоремой о непрерывности суперпозиции. Если допускает отрицательные значения 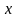для функции y=x^ , то для доказательства непрерывности этой функции при 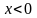функцию можно представить в виде: 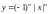. Непрерывность в нуле рекомендуется попробовать доказать самостоятельно (непосредственно по определению).

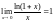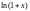
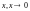5). . Другими словами,  или

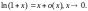
Доказательство. Функция 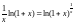непрерывна, как суперпозиция непрерывной и имеющей предел функции: 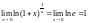. Аналогично доказывается, что

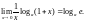
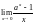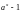
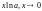6) = ln a . Другими словами,  или .

Доказательство. Обозначим a^x - 1=y, тогда x ln a=ln(1+y),

Стремление к нулю x 0 эквивалентно стремлению к нулю y 0,

 .

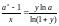
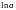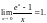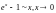Пример 1 (Следствие из предыдущего примера). Таким образом, или .

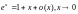Пример 2. Вычислить предел .

.

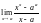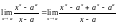Отдельно вычислим пределы и

= = =

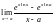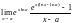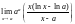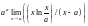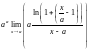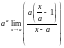= = = = =a^a ,

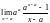= =a^aln a .

=a^a(ln a + 1).

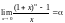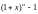
7) . Таким образом,  или .

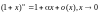Доказательство. Обозначим (1+x)^ - 1=y, тогда  ln(1+x) = ln(1+y).

 .

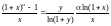
Пример 3. Вычислить предел .

.

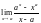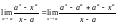Отдельно вычислим пределы и

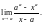
= =a^a ln a,

=- = =

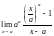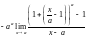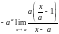= =-a^a.

= a^a(ln a - 1).

8) Вычислить предел .

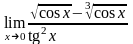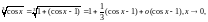
тогда

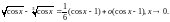
Поэтому .

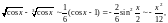
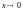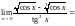
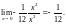
9) Непрерывность .

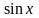|sin x –sin x₀|=2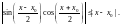

Непрерывность cos x следует из свойств непрерывных функция: cos x = sin(x+/2).

Непрерывность тригонометрических функция tg x, ctg x, arcsin, arcos, arctg, arcctg в своих областях определения следует из свойств непрерывных функций. Например, tg x непрерывен для всех кроме точек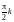 , в которых имеется разрыв второго рода.

10) f=const, многочлен P_n(x)=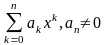 является непрерывными функциями всюду, рациональная функция

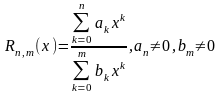непрерывна всюду, кроме нулей знаменателя.