4º. Вычисление скорости и ускорения при естественном способе задания движения.
По
определению скорости материальной
точки можем записать
.
Здесь
– движение точки
,
заданное векторным способом;
– ее скорость в момент времени
.
Согласно
связи векторного способа с естественным
имеем
=
,
где
– естественная параметризация траектории
движения, а
– закон движения по этой траектории.
Дифференцируя
по
,
получаем
=
,
(15)
где — орт касательной к траектории в той ее точке, с которой совпадает положение материальной точки в момент времени .
Из (15) можем сделать следующие заключения:
а) скорость параллельна — орту касательной к траектории в том
положении точки , которое она занимает в момент времени ;
б)
=
.
Обратимся
теперь к выводу формулы для вычисления
ускорения
материальной точки. По определению
имеем
=
.
Подставляя правую часть (15) вместо
и
дифференцируя по
,
получим
=
=
+
=
+
.
Воспользуемся
формулой Френе
=
=
,
где
– орт главной нормали к траектории в
том положении, которое занимает на ней
точка
в момент времени
;
– кривизна, а
– радиус кривизны траектории в этом
положении. Тогда выражение для
примет вид:
=
+
=
+
.
(16)
Вектор
=
называется касательным
(тангенциальным) ускорением
точки
,
а вектор
=
=
– ее нормальным
ускорением.
Величина скорости обозначена = = . Формула (16) составляет предмет теоремы Гюйгенса.
Теорема Гюйгенса.
Вектор мгновенного ускорения точки (ускорения в момент времени ) находится в соприкасающейся плоскости к траектории ее движения и равен векторной сумме касательного (тангенциального) ускорения = и нормального ускорения = .
5º. Кинематический способ вычисления кривизны кривой.
Из теоремы Гюйгенса имеем:
=
=
=
.
(17)
Покажем,
что 
=
=
.
Действительно,
из (15) находим
=
.
Тогда, дифференцируя это равенство по
,
получим
=
.
Возводим в квадрат и, учитывая, что = , приходим к соотношению
=
.
Отсюда следует = .
Таким
образом, формула (17)
позволяет вычислить радиус кривизны,
если известны
,
и
.
На ее основе можно предложить следующий
алгоритм расчета
.
Алгоритм построения радиуса кривизны кривой.
Пусть кривая задается параметрически:
, 
,
,
.
(18)
1).
Задаем какое-либо движение по кривой:
.
Например, в качестве
берем функцию
.
2).
Вычислим величины
и
.
Очевидно, можем записать:
=
,
=
,
=
.
Здесь
, 
, 
— заданные функции (18). Отсюда получаем
формулу для вычисления величины
,
стоящей в правой части соотношения (17),
=
.
Аналогично, имеем
=
=
,
=
=
,
=
=
.
По
формуле
=
,
подставляя соотношения (18),
находим величину
,
стоящую под корнем в правой части
выражения (17).
3). Вычислим величину . Формулу для ее расчета получаем через последовательность следующих очевидных соотношений
=
=
=
=
.
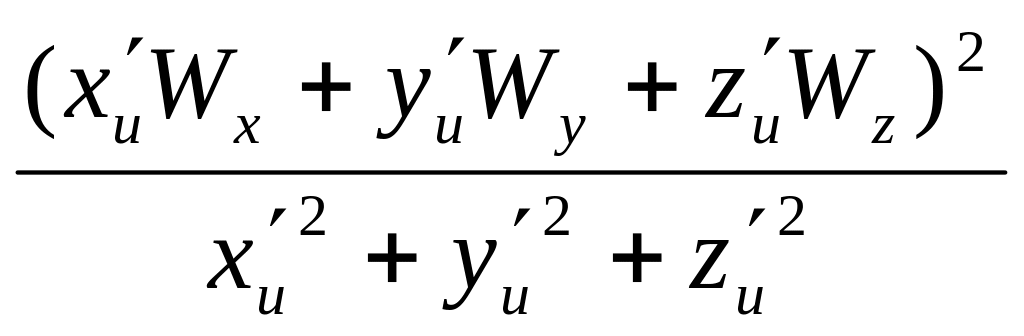4). Подставляя в выражение для радиуса кривизны (17)
=
вычисленные значения , , , получим требуемое.
Применение алгоритма рассмотрим на примере вычисления радиуса кривизны эллипса в любой его точке.
Уравнение эллипса в декартовых координатах имеет вид:
.
Переходим
к параметрическому уравнению эллипса:
,
.
Задаем закон движения по эллипсу: . Тогда
1).
=
=
,
=
=
, 
.
2).
=
,
=
,
=
.
3).
=
(
+
)
(
)
.
Подставляя , и = в (17), получим формулу для вычисления радиуса кривизны эллипса в любой его точке
=
=
.
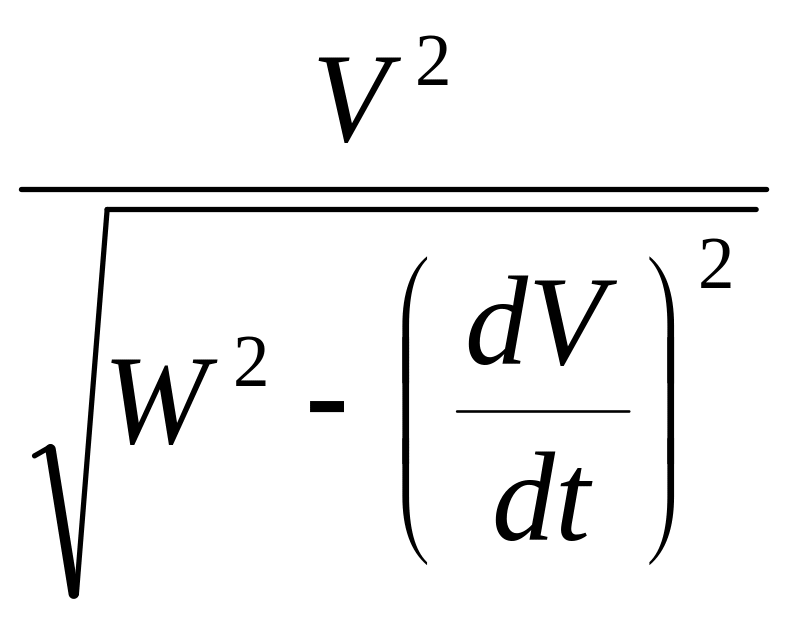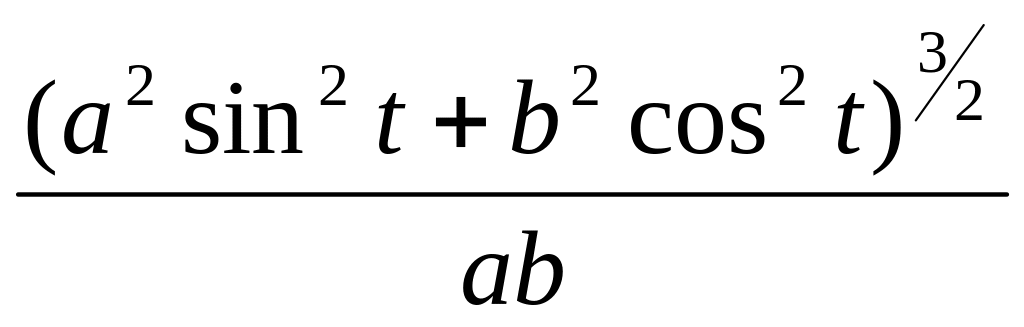В декартовых координатах она будет иметь вид
=
.
(19)
В
частности, если
,
то эллипс вырождается в окружность.
Тогда
,
и из (19) получим
=
в любой точке окружности.
Пусть
.
Вычисляем
в вершинах эллипса. В вершинах на оси
имеем
.
Для них из (19) получим
=
.
В
вершинах на оси
имеем
.
Из (19) следует, что в них
=
.