
- •Томский государственный университет систем управления и радиоэлектроники (тусур) Кафедра промышленной электроники (прэ)
- •Программирование
- •Введение
- •Модель цепи в пространстве состояний.
- •Получение модели цепи в пространстве состояний на основе системы уравнений Кирхгофа.
- •Пример построения модели цепи в пространстве состояний
- •Получение компонентов модели цепи в пространстве состояний на основе матричных операций MathCad
- •Аналитическое решение систем линейных дифференциальных уравнений.
- •Матричная экспонента
- •Некоторые свойства матричной экспоненты
- •Матричная экспонента и преобразование подобия
- •Собственные числа и собственные вектора матрицы
- •Расчет матричной экспоненты на основе преобразования подобия с использованием функций MathCad
- •Решение системы дифференциальных уравнений с использованием матричной экспоненты в MathCad.
- •Собственные числа, колебательный характер переходного процесса и резонансные явления.
- •Рекомендации по выбору значений параметров элементов схемы
- •Расчет реакции схемы на ступенчатое воздействие
- •Реакция цепи на одиночный прямоугольный импульс
- •Реакция цепи на периодическую последовательность прямоугольных импульсов
- •Получение осциллограмм установившегося режима.
- •Трассировка графиков
- •Задание на курсовое проектирование
- •Построение графического изображения схемы
- •Построение системы уравнений Кирхгофа
- •Формирование регионов с определениями основных функций
- •Выбор значений параметров элементов схемы, обеспечивающих колебательный переходный процесс
- •Исследование отклика цепи на включение источника эдс единичной амплитуды.
- •Исследование отклика цепи на прямоугольный импульс
- •Исследование установившегося процесса в цепи при воздействии периодической последовательности импульсов
- •Оформить пояснительную записку в виде файла MathCad с комментариями (см. «Приложение в»).
- •Приложение а
- •Приложение б
- •Приложение в
- •3.1 Операторы определений функций для расчета матричных
- •3.2 Формирование функций расчета матричной экспоненты
- •3.3 Определение функции расчета реакции цепи на включение
- •3.4 Определение функции расчета реакции цепи на одиночный
- •3.5 Определение функций расчета переходного процесса в цепи
- •3.6 Определение функций расчета переходного процесса в цепи
- •3.7 Построение функций, используемых при выборе величин
- •4. Задание численных величин параметров
- •5. Получение реакции цепи на включение единичного источника эдс
- •6. Получение реакции цепи на подключение к источнику эдс,
- •7. Получение реакции цепи на подключение к источнику эдс,
- •8. Получение графиков установившихся процессов при воздействии
Решение системы дифференциальных уравнений с использованием матричной экспоненты в MathCad.
Рассмотрим следующую последовательность операторов MathCad:
![]()
![]()
![]()
![]()
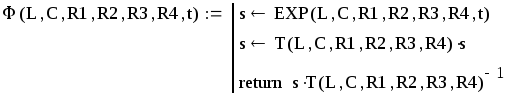
Здесь представлены функции, предназначенные для аналитического решения системы дифференциальных уравнений (1.11) Полагаем, что рассматриваемой последовательности операторов предшествует фрагмент кода, рассмотренный в п.1.3 и функции расчета необходимых матриц введены.
Первым следует оператор определения скалярной «физически реализуемой» экспоненты EX(a,t), за ним идут операторы задания функций расчета вектора собственных чисел Λ(L,C,R1,R2,R3,R4) и матрицы собственных векторов T(L,C,R1,R2,R3,R4). Заметим, что у этих функций сохранен тот же список аргументов, что и у функции расчета матрицы системы. Это связано с тем, что в применяемых встроенных функциях eigenvals и eigenvecs в качестве матрицы-аргумента используется результат работы функции A(L,C,R1,R2,R3,R4). У вводимых далее функций список аргументов еще более удлиняется, дополняясь временем t. Последний оператор в этом фрагменте определяет функцию расчета матричной экспоненты Ф(L,C,R1,R2,R3,R4,t).
На рисунке 2.1 приведены графики функций времени - элементов матричной экспоненты. Матричная экспонента рассчитана при следующих значениях параметров:
R1= 10 ом; R2 = 400 ом; R3 = 5 ом; R4=800 ом;
L=0.025 гн; C=510-6 Ф.
При таком сочетании параметров собственные числа матрицы A являются комплексными и образуют комплексно-сопряженную пару:
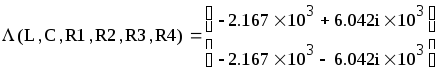 ,
,
что обусловливает колебательный характер переходного процесса в цепи, наблюдающийся на графиках рис. 2.1.
Функции, представленные на графиках являются решениями однородного ДУ. Составляющие матричной экспоненты Ф(L,C,R1,R2,R3,R4,t)0,0. и Ф(L,C,R1,R2,R3,R4,t)1,0. представляют собой колебания iL(t) и Uc(t), соответственно, при начальных условиях iL(0) = 1А и Uc(0) = 0.
Функции Ф(L,C,R1,R2,R3,R4,t)0,1. и Ф(L,C,R1,R2,R3,R4,t)1,1.- это те же iL(t) и Uc(t), но при начальных условиях iL(0) = 0 и Uc(0) = 1 V.
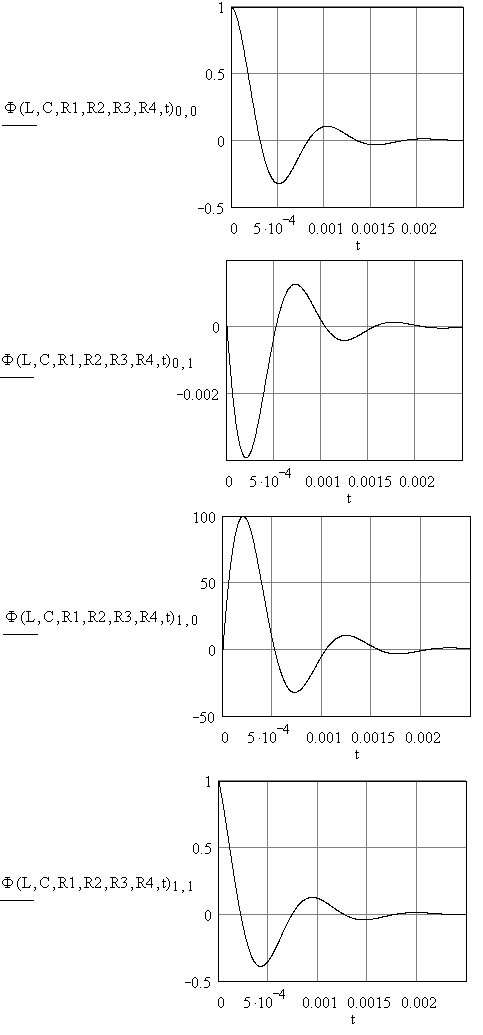
Рис. 2.1. Составляющие матричной экспоненты
Собственные числа, колебательный характер переходного процесса и резонансные явления.
В случае некратных собственных чисел матрицы A, любая компонента решения системы однородных ДУ xi(t), представляющая переходный процесс, выражается линейной комбинацией экспонент:
![]() , (2.34)
, (2.34)
где λk – собственные числа матриц A;
qik – постоянные числа;
n – порядок системы ДУ, размер матрицы A.
Для всех вариантов схем предлагаемого курсового проекта порядок системы ДУ равен 2.
Собственные числа могут быть вещественными или образовывать комплексно – сопряженные пары.
В случае комплексно – сопряженных собственных чисел λ1,2 переходный процесс образован синусоидами вида:
UeRe(λ)t sin(Im(λ)t +φ),
где λ – любое из комплексно – сопряженных чисел λ1 или λ2,
Re(λ) и Im(λ) реальная и мнимая части λ,
U и φ – постоянные величины, не зависящие от λ.
Величину ω0 = Im(λ) называют угловой частотой собственных колебаний, величину α = Re(λ), при α < 0, называют затуханием переходного процесса. Иногда для характеристики процесса вместо α используют обратную ей величину – постоянную времени τ, имеющую размерность времени:
![]() . (2.35)
. (2.35)
Очевидно, чем больше τ , тем медленнее затухает переходный процесс. Величина τ – это промежуток времени, за который амплитуда составляющей переходного процесса, связанной с данным λ уменьшиться в e раз.
С круговой частотой ω0 связана обычная частота f0 , измеряемая в герцах, и период собственных колебаний T0, измеряемый в секундах:
![]() (2.36)
(2.36)
Очевидно, что при | Im(λ)| = 0 (случай чисто вещественных собственных чисел), колебаний в переходном процессе не будет, и он будет иметь апериодический характер.
Как отмечалось в п. 1, в схемах с колебательным переходным процессом и периодическим внешним воздействием наблюдается явление резонанса, когда период внешнего воздействия и период собственных колебаний будут находиться в целочисленном соотношении, в частном случае, когда эти периоды совпадут.
В дальнейшем нас будут интересовать схемы с резонансом, т.е. схемы с колебательным характером переходного процесса. Этого необходимо достигнуть выбором величин сопротивлений.
