
- •Томский государственный университет систем управления и радиоэлектроники (тусур) Кафедра промышленной электроники (прэ)
- •Программирование
- •Введение
- •Модель цепи в пространстве состояний.
- •Получение модели цепи в пространстве состояний на основе системы уравнений Кирхгофа.
- •Пример построения модели цепи в пространстве состояний
- •Получение компонентов модели цепи в пространстве состояний на основе матричных операций MathCad
- •Аналитическое решение систем линейных дифференциальных уравнений.
- •Матричная экспонента
- •Некоторые свойства матричной экспоненты
- •Матричная экспонента и преобразование подобия
- •Собственные числа и собственные вектора матрицы
- •Расчет матричной экспоненты на основе преобразования подобия с использованием функций MathCad
- •Решение системы дифференциальных уравнений с использованием матричной экспоненты в MathCad.
- •Собственные числа, колебательный характер переходного процесса и резонансные явления.
- •Рекомендации по выбору значений параметров элементов схемы
- •Расчет реакции схемы на ступенчатое воздействие
- •Реакция цепи на одиночный прямоугольный импульс
- •Реакция цепи на периодическую последовательность прямоугольных импульсов
- •Получение осциллограмм установившегося режима.
- •Трассировка графиков
- •Задание на курсовое проектирование
- •Построение графического изображения схемы
- •Построение системы уравнений Кирхгофа
- •Формирование регионов с определениями основных функций
- •Выбор значений параметров элементов схемы, обеспечивающих колебательный переходный процесс
- •Исследование отклика цепи на включение источника эдс единичной амплитуды.
- •Исследование отклика цепи на прямоугольный импульс
- •Исследование установившегося процесса в цепи при воздействии периодической последовательности импульсов
- •Оформить пояснительную записку в виде файла MathCad с комментариями (см. «Приложение в»).
- •Приложение а
- •Приложение б
- •Приложение в
- •3.1 Операторы определений функций для расчета матричных
- •3.2 Формирование функций расчета матричной экспоненты
- •3.3 Определение функции расчета реакции цепи на включение
- •3.4 Определение функции расчета реакции цепи на одиночный
- •3.5 Определение функций расчета переходного процесса в цепи
- •3.6 Определение функций расчета переходного процесса в цепи
- •3.7 Построение функций, используемых при выборе величин
- •4. Задание численных величин параметров
- •5. Получение реакции цепи на включение единичного источника эдс
- •6. Получение реакции цепи на подключение к источнику эдс,
- •7. Получение реакции цепи на подключение к источнику эдс,
- •8. Получение графиков установившихся процессов при воздействии
Аналитическое решение систем линейных дифференциальных уравнений.
Аналитическое решение дифференциальных уравнений (ДУ) возможно далеко не во всех случаях. Наиболее общие результаты в плане построения аналитического решения получены для систем линейных ДУ.
![]() (2.1)
(2.1)
где
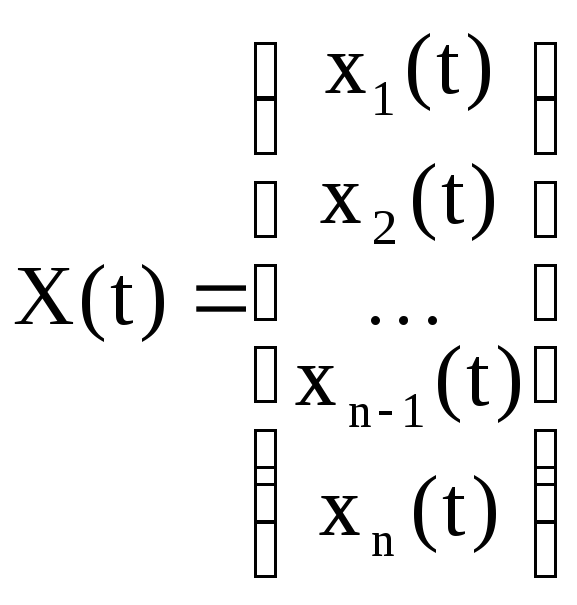 -
вектор-функция
искомых решений;
-
вектор-функция
искомых решений;
матрицы
постоянных коэффициентов
 -
-
 -
известная
вектор-функция внешних воздействий.
-
известная
вектор-функция внешних воздействий.
Из курса математики известно, что решение неоднородного ДУ (2.1) может быть получено в форме интеграла наложения (или интеграла Дюамеля):
![]() , (2.2)
, (2.2)
где Ф(t) – матричная (n×n) функция времени;
Х0 – вектор начальных условий.
Матричная функция Ф(t) известна в приложениях под многими названиями: переходная матрица системы, импульсная реакция системы, матрица фундаментальных решений системы однородных ДУ и т.п. Системы, представленные математической моделью (2.1), подразделяют в зависимости от поведения Ф(t) на
-
устойчивые, если Ф(t) → 0 при t→∞;
-
неустойчивые, если Ф(t) → ∞ при t→∞;
-
физически реализуемые, если Ф(t) ≡ 0, при t <0;
-
физически нереализуемые. если Ф(t) ≠ 0, при t <0.
Понятие физической реализуемости связано с невозможностью систем реагировать на воздействие до его появления, реальная система не может «предчувствовать» будущие внешние воздействия. Функцию Ф(t) можно представить как «интенсивность» памяти о величине воздействия по прошествии времени t с момента его возникновения. Чем медленнее затухает Ф(t), тем больший вес имеют прошедшие воздействия в текущем Х(t). Таким образом, чтобы исключить инверсию «памяти» в будущее, для физически реализуемых систем требуется дополнительное определение Ф(t) ≡ 0 для отрицательных t.
В выражении (2.2) первое слагаемое соответствует решению однородного ДУ, т.е. при f(t) ≡ 0:
![]() при
Ф(0) = I, (2.3)
при
Ф(0) = I, (2.3)
где
 ,–
единичная матрица,
,–
единичная матрица,
второе – решение неоднородного ДУ
Матричная экспонента
Функция Ф(t) играет важную роль в теории линейных дифференциальных уравнений. Она имеет специальное название – матричная экспонента, и обозначается как eAt. Свое название функция получила из-за ряда аналогий с обычной скалярной экспоненциальной функцией eat.
Известно, что решением скалярного ДУ первого порядка
![]() при
начальном условии y(0) = 1 является
экспонента eat
. Сопоставляя этот факт и (2.3), можно
отметить формальную аналогию. Эта
аналогия распространяется значительно
дальше.
при
начальном условии y(0) = 1 является
экспонента eat
. Сопоставляя этот факт и (2.3), можно
отметить формальную аналогию. Эта
аналогия распространяется значительно
дальше.
Для скалярной экспоненты имеет место разложение в степенной ряд
![]() .
.
Если в этом ряду заменить скалярную величину а на квадратную матрицу А и единицу на единичную матрицу Е, получим степенной ряд для матричной экспоненты:
![]() (2.4)
(2.4)
Соотношение (2.4) используют как одно из возможных определений матричной экспоненты.
Некоторые свойства матричной экспоненты
Отметим некоторые свойства матричной экспоненты eAt , вытекающие из ее представления рядом (2.4).
1) Матричная экспонента eA существует только для квадратных матриц A, т.е. таких матриц, у которых число строк равно числу столбцов.
2) Матричная экспонента eA – это квадратная матрица тех же размеров, что и A.
3)Дифференцирование матричной экспоненты по t:
![]() , (2.5)
, (2.5)
Соотношение (2.3) следует из (2.5) как частный случай при n =1.
4) Интегрирование матричной экспоненты по t:
![]() (2.6)
(2.6)
или
![]() (2.7)
(2.7)
Повторное n-кратное интегрирование матричной экспоненты по времени приводит к более общей формуле:
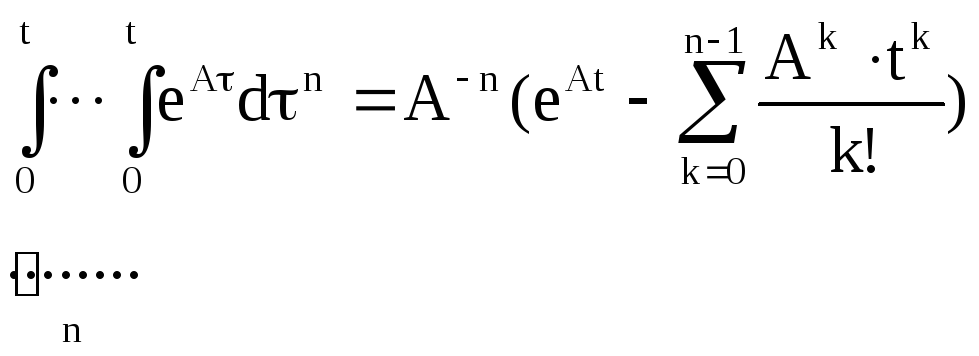 (2.8)
(2.8)
5) Матричная экспонента eA перестановочна с матрицей – аргументом:
AeA = eAA (2.9)
(из курса математики известно, что далеко не всякие матрицы обладают свойством перестановочности)
6) Для матричной экспоненты справедливо соотношение:
eA∙(t1+t2) = eA∙t1 ∙ eA∙t2 (2.10)
7) Если матрица A диагональная, т.е.:
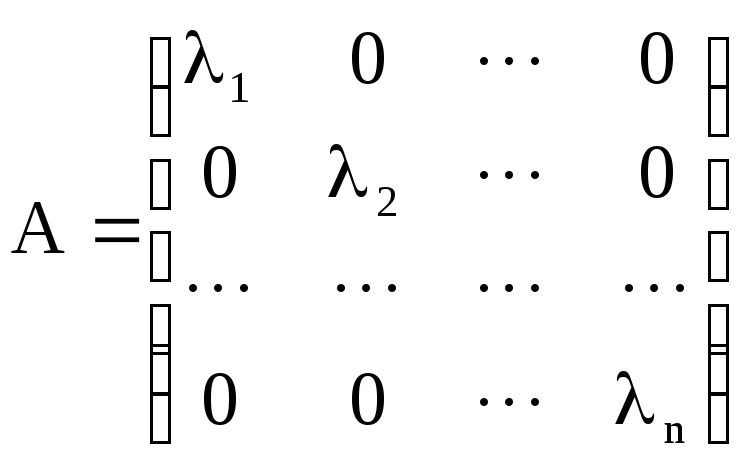 ,
,
то и матричная экспонента тоже диагональная и имеет вид:
 . (2.11)
. (2.11)
