Пример построения модели цепи в пространстве состояний

П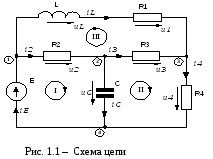усть имеется схема цепи с одним внешним воздействием в виде источника ЭДС E(t), показанная на рисунке 1.1 .

В схеме имеется 6 ветвей и 4 узла, после разметки выделено 3 контура.

Из курса ТОЭ известно, что для такой цепи можно составить 6 уравнений: 3 для баланса токов в узлах (I закон Кирхгофа) и 3 для баланса напряжений в контурах(II закон Кирхгофа).

Запишем систему уравнений Кирхгофа для этой цепи с учетом компонентных соотношений.

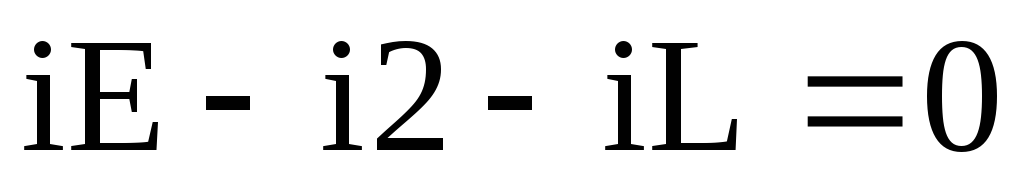
1. для узла 1:

2. для узла 2:

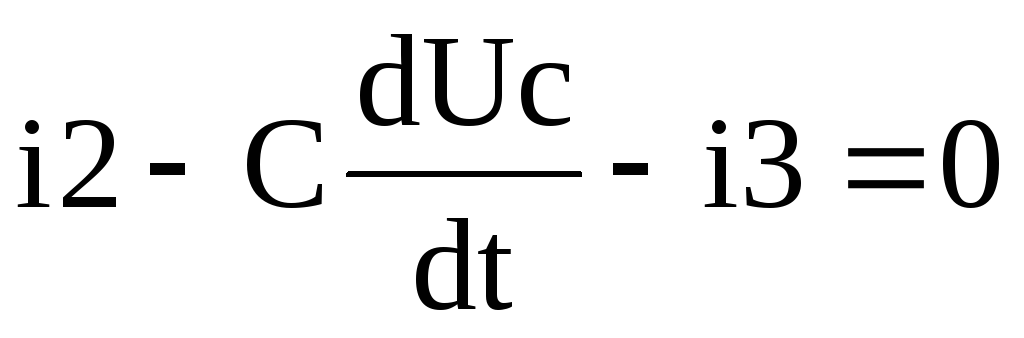
3. для узла 3: 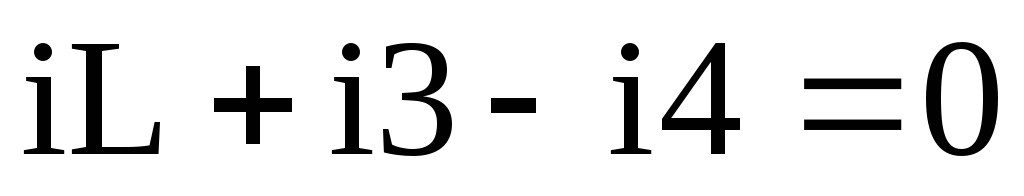(1.4)

4. для контураI:

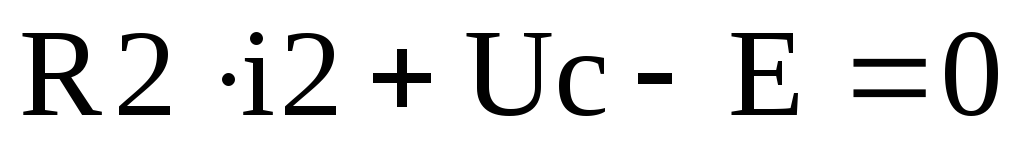
5. для контураII:

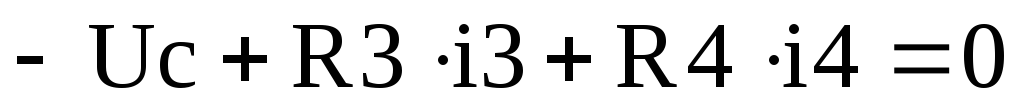
6. для контураIII:

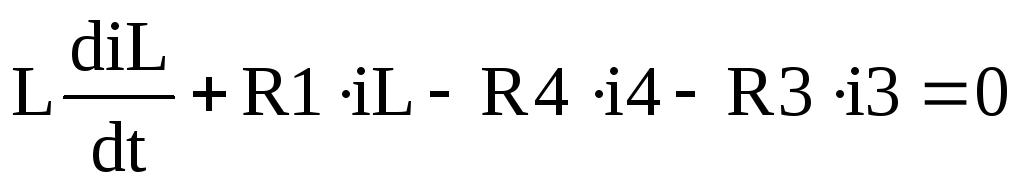
Система уравнений (4) связывает 9 переменных:

При правильной записи уравнений Кирхгофа получается система независимых уравнений, и можно выразить любые 6 переменных через оставшиеся 3.Поставим задачу выразить переменные через .

Воспользуемся для такого выражения средствами матричной алгебры математического процессора MathCad (см. п.2.4 и п.3.5 в [1]). Представим систему (1.4) в матричной форме:

X∙D = 0, (1.5)

где D – прямоугольная матрица 96 (9 столбцов и 6 строк),

X – вектор-столбец из 9 компонент.

Д

(1.6)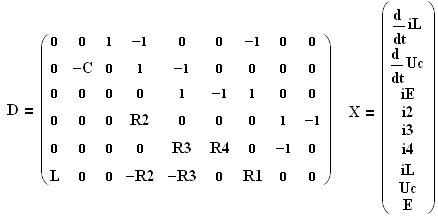

ля нашего примера матрица D и вектор X будут иметь вид:

Преобразуем (1.5) к такому виду:

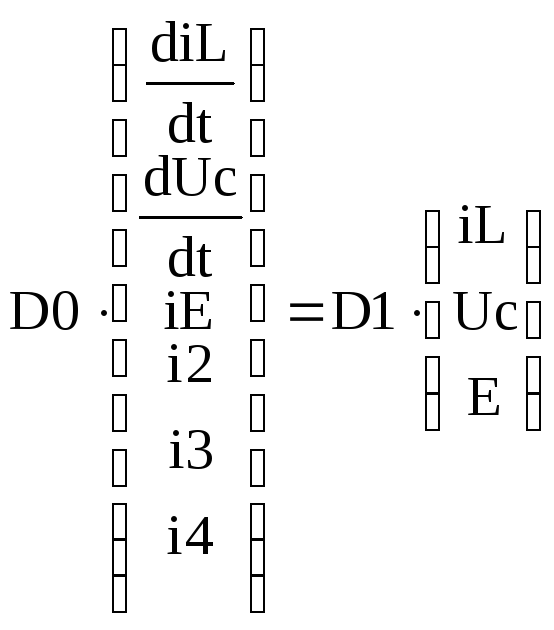, (1.7)

где матрицы D0 и D1для рассматриваемого примера имеют вид:

(1.8)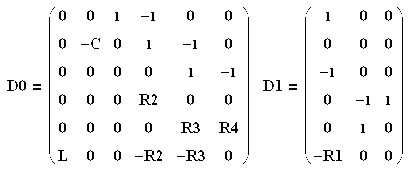

В виду того, что исходная система уравнений линейно независима, матрица D0 имеет обратную, поставленная выше задача имеет единственное решение:

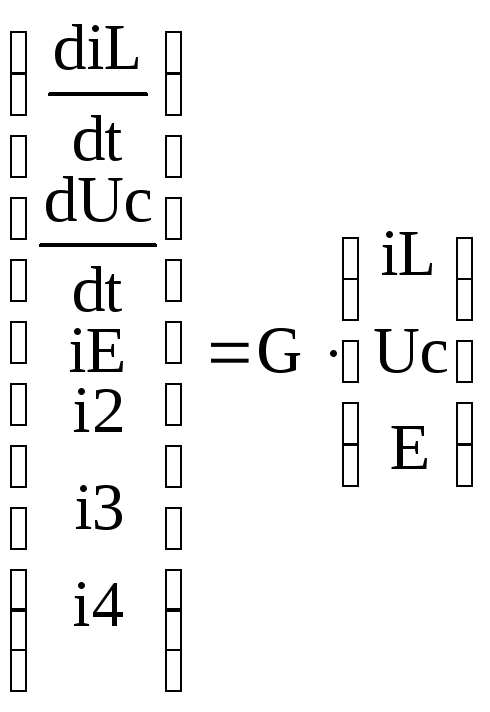, (1.9)

где G = D0^-1∙D1 – матрица 6×3 (6 строк и 3 столбца)

В нашем случае матрица G имеет вид:

(1.10)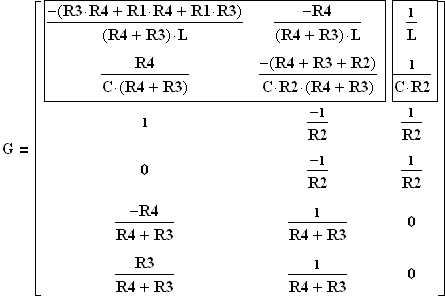

В системе уравнений (1.9) первые два уравнения дифференциальные, остальные – алгебраические. В выражении (1.10) прямоугольниками выделены компоненты матрицы G, представляющие параметры системы дифференциальных уравнений – модель цепи в пространстве состояний. Выпишем в явной форме систему дифференциальных уравнений:

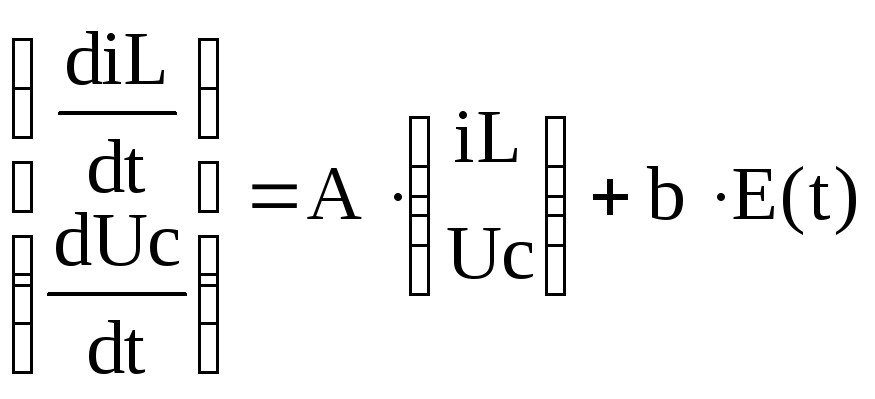, (1.11)

где

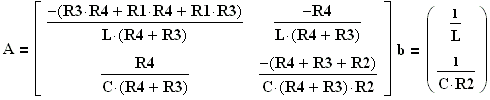
Решение уравнений (1.11) позволяет найти процессы iL(t) и Uc(t). Оставшиеся алгебраические уравнения системы (1.9) дают выражения токов в ветвях схемы в виде линейной комбинации процессов iL(t), Uc(t) и E(t).

Как правило, модель цепи в пространстве состояния помимо дифференциальных уравнений (ДУ), определяющих ее динамику, включает еще и т.н. уравнения наблюдения. Уравнения наблюдения – это выражения токов, протекающих через какие-либо заданные элементы, и/или напряжений между заданными точками схемы.

Пусть в нашем примере наблюдаемыми величинами являются ток через емкость и напряжение на резисторе R4. Согласно компонентным соотношениям

U_R4 = R4∙i4 и .

Получим выражения для наблюдаемых переменных U_R4 и i_C, используя выражения для i4 и из (1.9):

(1.12)

или в матричной форме:

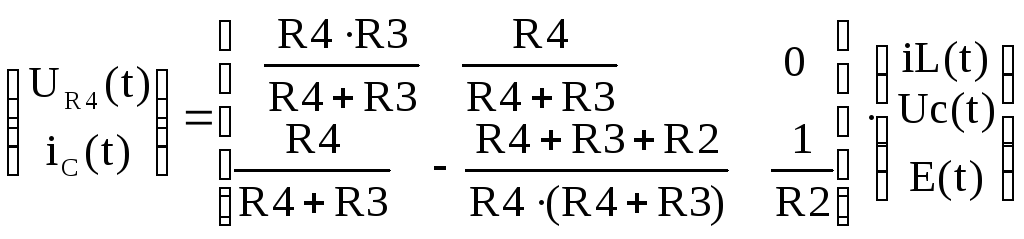(1.13)

Уравнения (1.11 – 1.13) представляют собой полную модель цепи в пространстве состояний. Дальнейшее решение задачи сводится к отысканию решения системы ДУ (1.11).

Получение компонентов модели цепи в пространстве состояний на основе матричных операций MathCad

Для построения модели цепи в пространстве состояний необходимо получить ряд матриц:

A – матрицу системы ДУ;

b – вектор коэффициентов перед функцией внешнего воздействия E(t);

K – матрицу наблюдения, связывающую наблюдаемые переменные с переменными состояния.

Эти составляющие модели могут быть получены с помощью операторов и встроенных функций MathCad. Ниже приводится последовательность операторов, позволяющих сформировать необходимые матрицы.

Первым создается оператор определения матричной функции, задающий матрицу системы уравнений Кирхгофа (1.6):

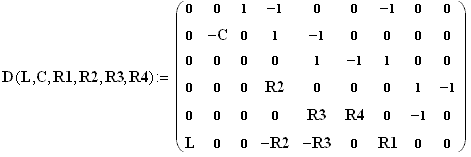
Далее следуют операторы, определяющие функции формирования подматриц D0 и D1 из (1.8):

В этих операторах использована функция submatrix из библиотеки MathCad. Эти функция выделяет прямоугольный блок заданного размера из матрицы, записанной первым аргументом. В данном случае это матрица, возвращаемая функцией D(L,C,R1,R2,R3,R4).

Затем идет оператор расчета матрицы G из (1.10):

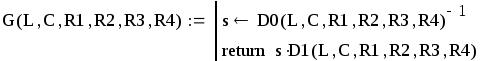
При попытке выполнить этот оператор может возникнуть коллизия из-за вырожденности матрицы D0. Эта ситуация может быть вызвана либо неверной записью системы уравнений Кирхгофа, либо ошибками при формировании исходной матрицы D.

Для проверки правильности выражений, предшествующих получению матрицы D0, можно вывести выражение для ее определителя в символическом виде. Это выражение должно иметь такую структуру, которая не позволяла бы ему обратиться в нуль при какой-либо комбинации значений параметров элементов схемы. В нашем примере выражение для определителя D0 имеет вид:

Очевидно, что такой определитель D0 не может обратиться в нуль ни при каких положительных значениях параметров элементов схемы.

Заметим, что здесь применен оператор символического вывода, дающий выражение в виде формулы. Этот оператор необходимо использовать до назначения параметрам конкретных значений.

За оператором определения функции, вычисляющей матрицу G, следуют операторы задания функций для расчета матрицы A и вектора b модели цепи в пространстве состояний:

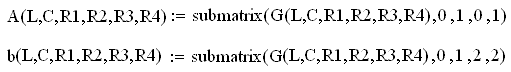
В этих операторах так же использованы библиотечные функции submatrix, выделяющие фрагмент матрицы – аргумента.

Завершают последовательность операторов формирования матриц модели операторы определения функций для расчета матрицы наблюдения:

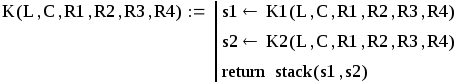
Функции K1 и K2 формируют строки матрицы наблюдения: K1 –

строку для выражения U_R3, K2 – строку для i_С. В этих функциях использован оператор выделения i – го столбца матрицы ^{< i >} . При формировании K1 из матрицы G^T выделяется столбец с номером 5, при формировании K2 из G^T выделяется столбец с номером 1. Напомним, что в MathCad по умолчанию установлена индексация массивов, начинающаяся с нуля.

Двойное применение операции транспонирования матриц связано с тем, что в MathCad есть только оператор выделения столбца матрицы, и нет оператора выделения строки. Поэтому для выделения i-й строки матрицы приходится сначала ее транспонировать, затем выделить в транспонированной матрице i-й столбец и еще раз транспонировать результат.

В функции расчета матрицы наблюдения K применена библиотечная функция stack, осуществляющая объединение однострочных матриц K1 и K2 в единую двухстрочную матрицу K.

Мы рассмотрели операторы – определения функций для получения всех элементов модели цепи в пространстве состояний. В каждой из построенных нами функций используется полный список аргументов, что в известной мере загромождает текст, делает операторы длинными, они не помещаются в стандартный формат документа.

Неудобство, вызванное длинными списками параметров у вводимых функций, компенсируется тем, что эти функции становятся независимыми друг от друга и впоследствии могут вызываться с набором фактических параметров, определенным непосредственно перед точкой вызова. Функции A(L,C,R1,R2,R3,R4), b(L,C,R1,R2,R3,R4) и K(L,C,R1,R2,R3,R4) будут использоваться в составе вводимых далее функций.