3.4.4. Оптимизация непараметрических моделей коллективного типа по коэффициенту размытости
Оптимизация
непараметрических моделей коллективного
типа по коэффициентам размытости
осуществляется по аналогии с п. 3.3.3. В
отличии от непараметрической оценки
регрессии рассматриваемые модели
коллективного типа формируются из
упрощённых параметрических аппроксимаций,
которые проходят через «опорные» точки,
количество которых
меньше объёма обучающей выборки
.
Поэтому при поиске оптимального
коэффициента размытости в качестве
контрольной выборки можно использовать
как «опорные» точки, так и точки обучающей
выборки за исключением опорных.
Пусть
- множество номеров «опорных» точек из
обучающей выборки, а
- множество номеров точек обучающей
выборки за исключением «опорных». Тогда
при реализации метода скользящего
экзамена и использовании «опорных»
точек в качестве контрольных
среднеквадратический критерий (3.13)
будет иметь вид
.
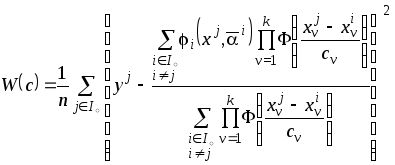При использовании обучающей выборки в качестве контрольной среднеквадратический критерий (3.13) имеет вид
.
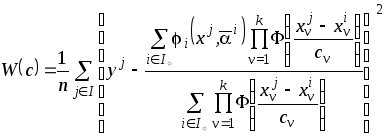При этом оптимальный набор коэффициентов размытости будет соответствовать
.
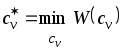3.5. Нелинейные непараметрические коллективы решающих правил в задаче восстановления стохастических зависимостей
Пусть дана выборка
из статистически независимых наблюдений
значений
неизвестной однозначной зависимости
(3.19) и её аргументов
.
Считается, что
функция (3.19) и плотности вероятности
,
в области определения
непрерывные и достаточно гладкие.
Идея предлагаемого подхода состоит в декомпозиции исходной задачи, построении семейства локальных решающих функций на основании однородных частей обучающей выборки и последующей их организации в едином нелинейном решающем правиле с помощью методов непараметрической статистики. Однородная часть обучающей выборки содержит её элементы, удовлетворяющие одному или нескольким требованиям, таким как наличие однотипных признаков (непрерывные, дискретные, лингвистические и др.), отсутствие либо наличие пропусков данных, что порождает широкий круг условий синтеза непараметрических решающих правил. Однородные части обучающей выборки могут отличаться размерностью и количеством элементов.
На основании
однородных частей обучающей выборки
сформируем наборы признаков
из исходных
и построим семейство частных моделей
на основании обучающих выборок
.
Интеграция частных моделей в нелинейном
коллективе решающих правил осуществляется
в соответствии с процедурой
,
(3.32)
где
,
- модели частных зависимостей
и объединяющего их нелинейного оператора
.
Структура предлагаемого коллектива решающих правил при восстановлении многомерной стохастической зависимости (3.19) представлена на рис. 3.8.
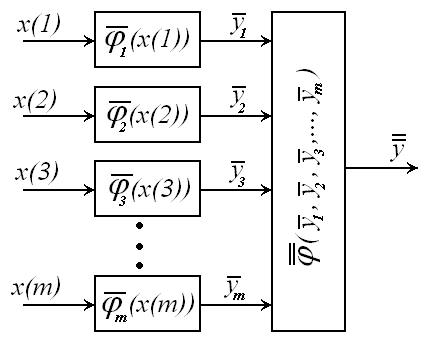
Рис. 3.8. Нелинейный непараметрический коллектив решающих правил (3.32)
с каскадной структурой
При построении
частных моделей
могут быть использованы известные
методы аппроксимации, включая
непараметрическую регрессию
,
,
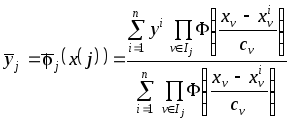(3.33)
где
- номера признаков, составляющих их
набор
;
- коэффициенты размытости ядерных
функций, значения которых зависят от
объёма выборки
.
Обобщение частных
моделей
в едином решающем правиле осуществляется
с помощью непараметрической статистики
,
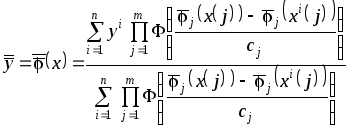(3.34)
формируемой по
выборке
.
Оптимизация
непараметрического коллектива (3.34) по
коэффициентам размытости ядерных
функций
производится в режиме «скользящего
экзамена» из условия минимума эмпирического
критерия
.
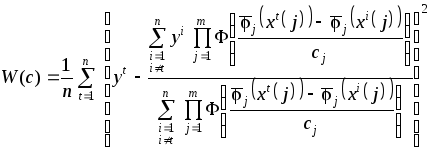Преимущества предлагаемой процедуры по сравнению с моделями типа «черный ящик» состоит в возможности учета частичных априорных сведений о виде взаимосвязи между переменными исследуемой зависимости и «обходе» проблем малых выборок за счет снижения размерности задачи.
Модификация нелинейного непараметрического коллектива решающих правил, основанного на учёте оценок показателей эффективности частных решающих правил.
Для повышения
аппроксимационных свойств коллектива
(3.34) предлагается дополнительно учитывать
показатели эффективности
частных решающих правил (3.33). Для этого
сформируем на основе исходных
обучающие выборки
,
в которых значения
определяются в соответствии с выражением
,
,
,
где
- частные модели (3.33) при оптимальных
коэффициентах размытости
,
.
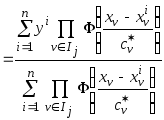Тогда нелинейный
коллектив частных моделей
,
представляется в виде
.
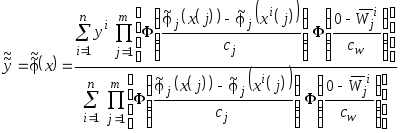Метод группового учёта аргументов, основанный на коллективе непараметрических регрессий.
Второе направление восстановления многомерных стохастических зависимостей (3.19) в условиях малых выборок основывается на модификации метода группового учёта аргументов в соответствии последовательной процедурой формирования решений
,
(3.35)
структура которой представлена на рис. 3.9.
Рис. 3.9. Нелинейный непараметрический коллектив решающих правил (3.35)
с последовательной структурой
Каждый
-й
этап формирования решений реализуется
с помощью непараметрической оценки
условного математического ожидания
,
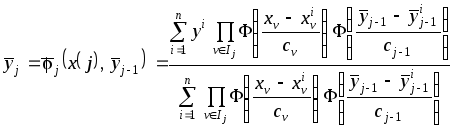(3.36)
где
.
Построение последовательной процедуры восстановления зависимости (3.35) предполагает выполнение следующих действий:
1. Определить набор
признаков, например
,
из исходных
,
который обеспечивает минимальную оценку
ошибки восстановления зависимости
(3.19). Модель
соответствует первому этапу обработки
информации.
2. Для конкретного
набора
,
сформировать обучающую выборку
и на этой основе построить модель типа
(3.33)
и оценить её эффективность.
3. Повторить этап
2 для различных наборов признаков
,
и определить набор, например
,
который в паре с
позволяет получить минимальную оценку
ошибки аппроксимации.
По аналогии формируются последующие этапы синтеза нелинейного непараметрического коллектива решающих правил в задаче восстановления стохастической зависимости.
Выбор числа групп
признаков
,
а так же их сочетание в группах может
производиться исследователем в
зависимости от специфики решаемой
задачи либо с использованием имитационного
алгоритма выбора рациональной структуры.