
- •3.1. Классификация методов восстановления стохастических зависимостей
- •3.2. Параметрические алгоритмы восстановления стохастических зависимостей
- •3.3. Непараметрическая оценка регрессии в задаче восстановления стохастических зависимостей
- •3.3.1. Асимптотические свойства непараметрической оценки регрессии
- •Распишем выражение
- •3.3.2. Оптимизация непараметрической оценки регрессии по виду ядерной функции
- •3.3.3. Оптимизация непараметрической оценки регрессии по коэффициенту размытости
- •3.4. Непараметрические модели коллективного типа в задаче восстановления стохастических зависимостей
- •3.4.1. Непараметрические модели коллективного типа, основанные на учёте оценки эффективности упрощённых аппроксимаций
- •3.4.2. Асимптотические свойства непараметрической модели коллективного типа
- •3.4.3. Оптимизация непараметрических моделей коллективного типа
- •3.4.4. Оптимизация непараметрических моделей коллективного типа по коэффициенту размытости
- •3.5. Нелинейные непараметрические коллективы решающих правил в задаче восстановления стохастических зависимостей
- •3.6. Гибридные модели в задаче восстановления стохастических зависимостей
- •3.7. Синтез и анализ гибридных моделей стохастических зависимостей в условиях наличия их частного описания
- •3.8. Непараметрические гибриды решающих правил в задаче восстановления стохастических зависимостей
- •3.9. Последовательные процедуры формирования решений, основанные на учёте функций невязок
- •3.10. Коллективы решающих правил, основанные на учёте их условий компетентности
- •Литература
- •Дополнительная литература
- •Контрольные вопросы
- •Контрольные упражнения
3.4. Непараметрические модели коллективного типа в задаче восстановления стохастических зависимостей
Структуру предлагаемых моделей составляют семейство упрощённых параметрических аппроксимаций искомой зависимости, не имеющих самостоятельного значения, которые строятся относительно системы «опорных» ситуаций из обучающей выборки. Объединение упрощённых аппроксимаций в коллектив реализуется с помощью непараметрической оценки оператора условного математического ожидания.
Пусть дана выборка
![]() из статистически независимых наблюдений
значений неизвестной функции
из статистически независимых наблюдений
значений неизвестной функции
![]() (3.19)
(3.19)
и её аргументов.
Преобразование
![]() и плотности вероятности
и плотности вероятности
![]() ,
,
![]() достаточно гладкие и имеют хотя бы
первые две производные.
достаточно гладкие и имеют хотя бы
первые две производные.
Поставим в
соответствие некоторым точкам обучающей
выборки
![]() ,
условно назовём их «опорными»,
упрощённые
параметрические аппроксимации
,
условно назовём их «опорными»,
упрощённые
параметрические аппроксимации
![]() (опорные функции) зависимости (3.19),
параметры которых удовлетворяют условиям
(опорные функции) зависимости (3.19),
параметры которых удовлетворяют условиям
![]() ,
(3.20)
,
(3.20)
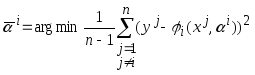 ,
,![]() ,
,
т.е.
![]() -я
упрощённая аппроксимация проходит
через
-я
упрощённая аппроксимация проходит
через
![]() ю
«опорную» точку и близка с среднеквадратическом
ко всем остальным элементам обучающей
выборки.
ю
«опорную» точку и близка с среднеквадратическом
ко всем остальным элементам обучающей
выборки.
Здесь и далее
опорные точки
![]() ,
выбираемые из выборки
,
выбираемые из выборки
![]() ,
упорядочиваются
,
упорядочиваются
![]() .
.
Упрощенные
параметрические аппроксимации
![]() могут быть линейными либо нелинейными.
могут быть линейными либо нелинейными.
Для линейных опорных функций
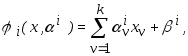 (3.21)
(3.21)
где параметры
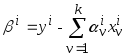 ,
а коэффициенты
,
а коэффициенты
![]() находятся из условия минимума критерия
находятся из условия минимума критерия
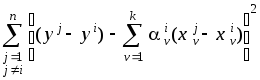 .
.
Тогда задача определения параметров может быть сведена к решению системы линейных уравнений
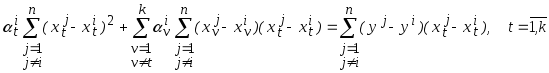
относительно
![]() ,
используя, например, правило Крамера
либо метод Гаусса.
,
используя, например, правило Крамера
либо метод Гаусса.
Например, при
![]()
![]() -я
линейная опорная функция имеет вид
-я
линейная опорная функция имеет вид
![]() ,
,
а система уравнений
для определения её коэффициентов (![]() )
представляется в матричном виде
)
представляется в матричном виде
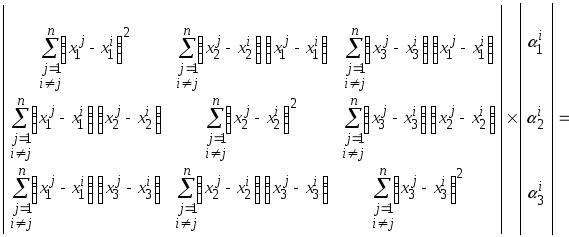
 ,
,![]() ,
,
где свободный член
![]() .
.
В одномерном
случае, когда
![]() является скаляром, значения
является скаляром, значения
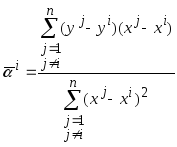 .
(3.22)
.
(3.22)
С целью уменьшения количества опорных аппроксимаций целесообразно усложнить их вид.
Для нелинейных опорных функций
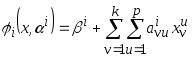 ,
(3.23)
,
(3.23)
где
![]() - количество признаков вектора входной
переменной
- количество признаков вектора входной
переменной
![]() ,
,
![]() - максимальная степень опорной
аппроксимации.
- максимальная степень опорной
аппроксимации.
Исходя из условия
прохождения опорной аппроксимации
через опорную точку параметр
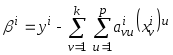 ,
а коэффициенты
,
а коэффициенты
![]() находятся из условия минимума критерия
находятся из условия минимума критерия
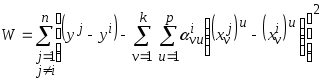 .
(3.24)
.
(3.24)
В одномерном
случае (![]() - скаляр), при максимальной степени
опорной аппроксимации
- скаляр), при максимальной степени
опорной аппроксимации
![]()
![]() .
.
Задача определения коэффициентов сводится к нахождению минимума критерия
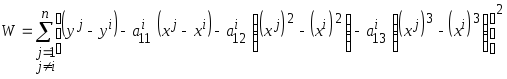
путём решения системы уравнений с помощью правила Крамера либо метода Гаусса
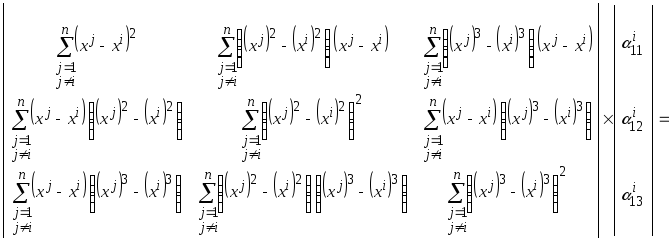
 ,
,
![]() ,
,
где свободный член
![]() .
.
Для многомерного
случая задача определения параметров
нелинейной опорной функции может быть
сведена к решению системы линейных
уравнений (![]() )
)
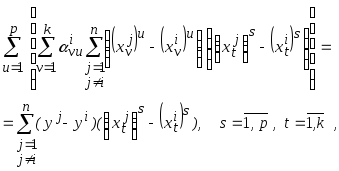
относительно
![]() .
.
Объединение упрощённых параметрических аппроксимаций в коллектив осуществляется на основе процедуры условного усреднения
 ,
(3.25)
,
(3.25)
где положительная,
ограниченная значением единица функция
![]() определяет «вес» правила
определяет «вес» правила
![]() при формировании решения в ситуации
при формировании решения в ситуации
![]() .
.
Примером функции
![]() является нормированное расстояние
между точками
является нормированное расстояние
между точками
![]() (основанная на преобразовании Евклидовых
расстояний)
(основанная на преобразовании Евклидовых
расстояний)
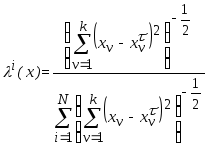
либо «весовая» функция
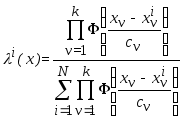 ,
(3.26)
,
(3.26)
составленная из
«ядерных» функций
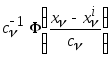 ,
на основе которых строятся непараметрические
модели.
,
на основе которых строятся непараметрические
модели.
Анализ непараметрических моделей коллективного типа.
Используем линейные
опорные аппроксимации (3.21) в коллективной
модели (3.25) при весовой функции
![]() (3.26). Рассчитаем коэффициент
(3.26). Рассчитаем коэффициент
![]() из условия прохождения упрощённой
аппроксимации
из условия прохождения упрощённой
аппроксимации
![]() через
через
![]() -ю
опорную точку
-ю
опорную точку
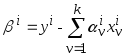 .
.
Подставим полученное
выражение
![]() в опорную аппроксимацию (3.21). В результате
имеем
в опорную аппроксимацию (3.21). В результате
имеем
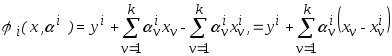 .
(3.27)
.
(3.27)
Полученную опорную аппроксимацию подставим в коллектив (3.25)
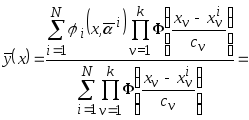
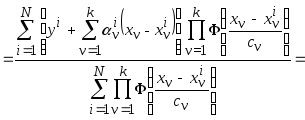
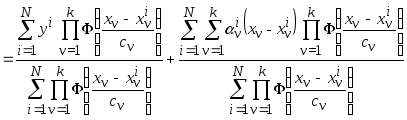 .
.
Несложно заметить, что непараметрическая модель коллективного типа (3.25) при линейных опорных функциях допускает представление в виде двух слагаемых
![]() ,
,
где первое слагаемое
![]() является непараметрической регрессией
(3.5), построенной по опорным точкам, а
второе
является непараметрической регрессией
(3.5), построенной по опорным точкам, а
второе
![]() - играет роль поправочного члена и
отражает условную взаимосвязь между
точками обучающей выборки, значения
которого снижаются по мере роста объёма
исходной информации. Причём, если
линейные опорные функции будут проходить
параллельно оси
- играет роль поправочного члена и
отражает условную взаимосвязь между
точками обучающей выборки, значения
которого снижаются по мере роста объёма
исходной информации. Причём, если
линейные опорные функции будут проходить
параллельно оси
![]() ,
что будет соответствовать
,
что будет соответствовать
![]() ,
тогда второе
слагаемое
,
тогда второе
слагаемое
![]() ,
а
,
а
![]() .
.
