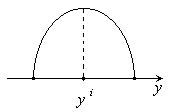3.3. Непараметрическая оценка регрессии в задаче восстановления стохастических зависимостей
Пусть дана выборка
статистически независимых наблюдений
случайной величины
,
распределённых с неизвестной плотностью
.
Априори вид искомой стохастической
зависимости (3.1) не задан. Необходимо
построить непараметрическую оценку
регрессии
,
если известно, что оператор связи
имеет однозначный характер.
Для того, чтобы построить хорошую модель по своим точностным характеристикам выберем среднеквадратический критерий
,
который характеризует
меру близости модели
к точкам обучающей выборки.
Найдём минимум
критерия
,
приравняв к нуль производную
.
В итоге получаем
.
Оптимальное решающее правило в смысле минимума среднеквадратического критерия представляется в виде условного математического ожидания
,
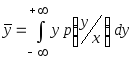(3.3)
где
- условная плотность вероятности, которую
можно записать в виде отношения
.
Подставим в вместо
и
их оценки плотности вероятности типа
Розенблатта-Парзена (2.2), получим
,
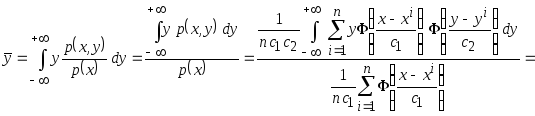
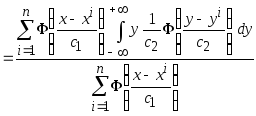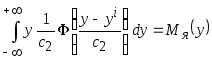- математическое
ожидание случайной величины
с ядерной плотностью
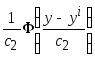(ядерная функция положительная,
симметричная и площадь под ней равна
единицы).
|
Рис. 3.3. Ядерная функция |
Учитывая, что ядерная функция является симметричной, получаем
т.к. ядерная
функция строится вокруг точки
|
,
.
Тогда непараметрическая оценка регрессии принимает вид
.
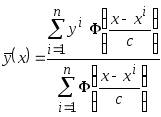(3.4)
Если
- многомерная случайная величина, то
непараметрическая оценка регрессии
запишется в виде
.
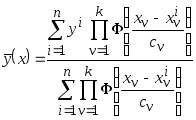(3.5)
Для трёхмерной
случайной величины
непараметрическая оценка регрессии
принимает вид:
.
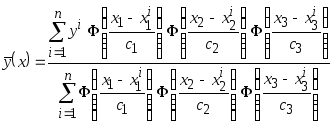С позиций принципов коллективного оценивания непараметрическая оценка регрессии является частным случаем коллектива
,
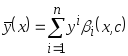(3.6)
где
.
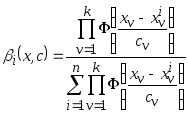В рассматриваемой
оценке наблюдения
восстанавливаемой функции играют роль
элементов коллектива, а многомерные
ядерные функции представляются в виде
их весов.
Непараметрическая регрессия с учётом мнения эксперта о качестве элементов обучающей выборки.
Пусть имеется
статистически независимых наблюдений
распределённых с неизвестной плотностью
.
Здесь
- оценка эксперта о «ценности» наблюдения
.
Априори вид искомой стохастической
зависимости (3.1) не задан.
Тогда в качестве оценки искомой зависимости можно воспользоваться непараметрической регрессией (3.5)
,
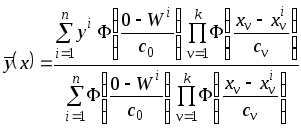где
.
Если
,
тогда значение
-го
наблюдения считается достоверно точным.
С увеличением значения
достоверность
значения
-го
наблюдения уменьшается.
3.3.1. Асимптотические свойства непараметрической оценки регрессии
Целью исследования асимптотических свойств является проверка сходимости непараметрической оценки регрессии типа (3.4) с увеличением объёма экспериментальных данных, к оптимальному решающему правилу (3.3).
Теорема 3.1.
Пусть: 1)
и
,
в области определения
ограничены и непрерывны со всеми своими
производными до второго порядка
включительно; 2) ядерные функции
являются положительными, нормированными
и симметричными, а также
;
3) последовательность
при
,
а
.
Тогда непараметрическая оценка регрессии
является асимптотически несмещённой
и состоятельной оценкой (3.3).
Доказательство.
Для упрощения
доказательства, предположим, что закон
распределения аргументов
известен. Тогда непараметрическая
оценка регрессии принимает (3.4) вид
.
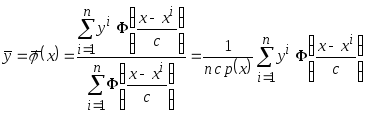(3.7)
-
Асимптотическая несмещённость
,
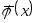при которой
.
Методика доказательства асимптотических свойств аналогична теореме 3.1.
Для проверки свойства несмещённости покажем, что
.
Подставим вместо
оценку (3.7)
.
Представим математическое ожидание в интегральной форме
.
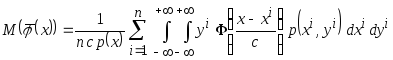Так как
наблюдения одной и той же случайной
величины
,
то
.
Тогда
.
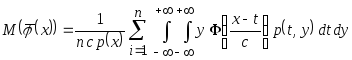Распишем совместную
плотность вероятности
в виде произведения
.
В результате получим
.
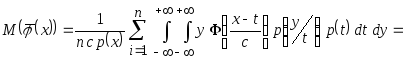
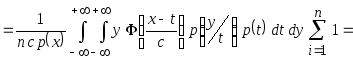
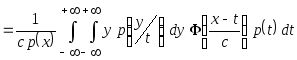Учитывая, что
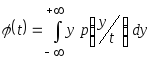- условное математическое ожидание
(3.3) и проведя замену переменных
,
,
и т.д., получаем
.
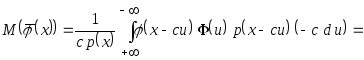
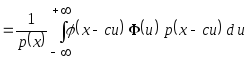Разложим функции
и
в ряд Тейлора в точке
.
Тогда
.
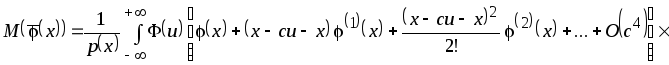
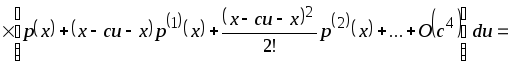
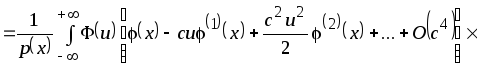
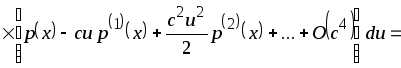
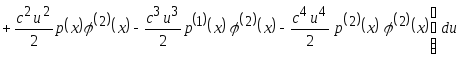Учитывая,
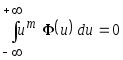при нечётном значении
и
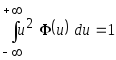(см. теорему 3.1).
После сокращений получаем выражение соответствующее асимптотической несмещённости
,
(3.8)
где
,
.
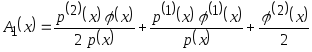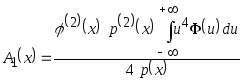Отсюда следует,
что непараметрическая оценка регрессии
в асимптотике (
)
стремится к оптимальному решающему
правилу (условному математическому
ожиданию) при
.
-
Сходимость в среднеквадратическом
.