Глава 3.

обучающиеся методы восстановления стохастических зависимостей

Задача аппроксимации стохастических зависимостей в исследовании систем возникает при построении статических моделей их элементов и оценивании показателей эффективности по экспериментальным данным. Для решения подобных задач существует множество методов, основанных на принципах обучения и имитации. В данной главе представлены обучающиеся модели восстановления стохастических зависимостей, использующие различные виды априорной информации: о локальном поведении , о виде зависимости , а также полезную информацию частных решающих правил.

3.1. Классификация методов восстановления стохастических зависимостей

Рассмотрим объект (рис. 3.1) с входом , который может быть вектором , и выходом y – скаляр.

Рис. 3.1. Объект исследования

Существует некоторая неизвестная взаимосвязь между входом и выходом . Необходимо оценить данную взаимосвязь, построив модель .

При восстановлении зависимости

(3.1)

в задачах идентификации статических объектов различают два типа исходной информации:

• структурные данные 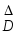, которые отражают априорные представления о виде ;

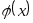• статистические данные 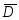, которые содержат сведения о наблюдении .

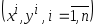На рис. 3.2 можно выделить три основных вида структурных данных, представляющих сведения о виде зависимости :

• область 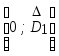- зависимость 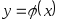существует;

• область 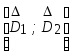- зависимость 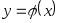однозначна, т.е. каждому 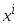соответствует одно значение ;

• область 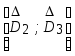- известна информация о виде зависимости (3.1) .

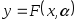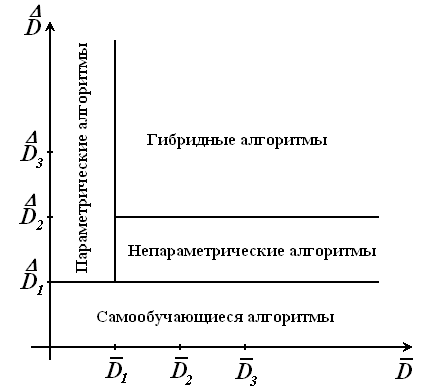
Рис. 3.2. Классификация моделей статических объектов

Параметрические алгоритмы применяются в том случае, если кроме обучающей выборки известна информация о виде искомой зависимости, т.е. исследователь знает или предполагает, что зависимость (3.1) может быть представлена в виде некоторого полинома ( - вектор параметров полинома). Тогда задача восстановления стохастической зависимости (3.1) сводится к определению неизвестных коэффициентов полинома.

Непараметрические алгоритмы ориентированы в основном на использование информации, содержащейся в точках обучающей выборки. Важным условием их применения является однозначность восстанавливаемой зависимости (3.1).

Гибридные модели используют сведения как о виде зависимости , так и информацию, содержащуюся в точках выборки . Также возможны ситуации, когда вместо информации о виде зависимости имеется «старая» модель зависимости (3.1) , которую необходимо скорректировать по новым данным , где .

На практике часто встречаются ситуации, когда искомые стохастические зависимости неоднозначны и имеют разрывы не только по своей природе, но и в следствии того, что существующая система контроля состояния объекта не даёт возможности измерять полный набор компонентов вектора входных переменных. Поэтому возникает задача создания подхода, позволяющего расширить круг решаемых задач моделирования. В этом случае используются самообучающиеся алгоритмы, где априорными сведениями является информация о существовании зависимости (3.1).

3.2. Параметрические алгоритмы восстановления стохастических зависимостей

Пусть дана статистически независимых наблюдений случайной величины , распределённых с неизвестной плотностью . Также имеется информация о виде искомой зависимости (3.1), представленная в полиномиальном виде . Необходимо построить параметрическую оценку регрессии , если известно, что оператор связи имеет однозначный характер.

Для простоты последующих выкладок предположим, что зависимость описывается полиномом

.

Задача восстановления стохастической зависимости (3.1) сводится к определению неизвестных коэффициентов полинома (, , ) из условия минимума квадратического критерия (3.2) с помощью метода наименьших квадратов.

Необходимо подобрать коэффициенты полинома таким образом, чтобы сумма квадратов отклонений полинома от экспериментальных точек была минимальна

. (3.2)

Для этого необходимо приравнять к нулю производные критерия (3.2) по , и :

,

,

.

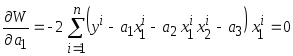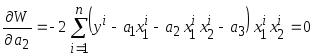После очевидных преобразований, полученную систему уравнений можно представить в матричном виде

.

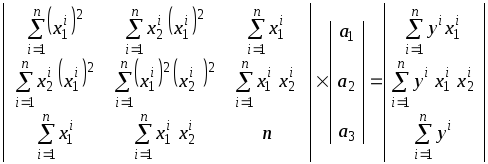Воспользовавшись методом Гаусса приводим матрицу к треугольному виду и находим неизвестные коэффициенты полинома.

В итоге получаем параметрическую оценку регрессии

,

где , , - рассчитанные коэффициенты.