Числовые характеристики случайных величин

< На прошлых занятиях мы познакомились с характеристиками присущими дискретным и непрерывным случайным величинам.

Для дискретных случайных величин это были: функция распределения, род распределения.

Для непрерывных случайных величин: функция распределения и плотность распределения. >

Среди числовых характеристик случайных величин необходимо прежде всего отметить те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.

Одной из таких характеристик положения является математическое ожидание случайной величины, которое иногда называют просто средним значением случайной величины.

Математическое ожидание обозначается буквой M[X] или m_x и определяется как

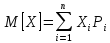
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

Приведенная формула для математического ожидания соответствует случаю дискретной случайной величины. Для непрерывной величины X математическое ожидание выражается не суммой, а интегралом:

,

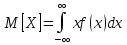где f(x) – плотность распределения.

Кроме математического ожидания на практике применяют т такие характеристики положения как мода и медиана.

Модой случайной величины называется ее наиболее вероятное значение.

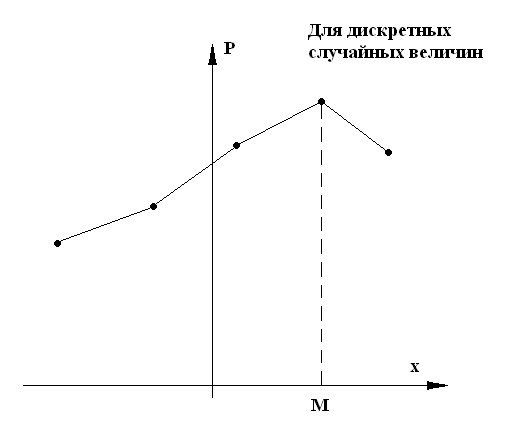
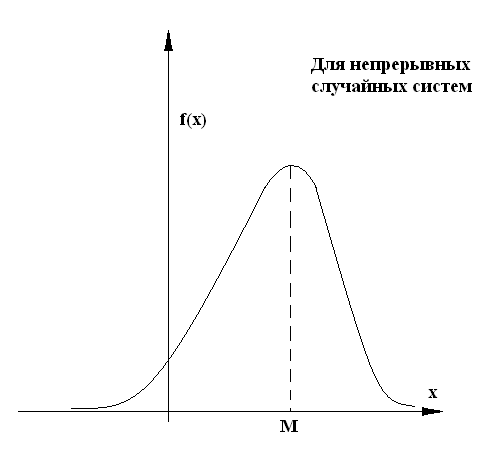
Рисунок 14 Рисунок 15

В случае непрерывной случайной величины модой является то значение, в котором плотность вероятности максимальна.

Если многоугольник распределения имеет более одного максимума распределение называется полимодельным.

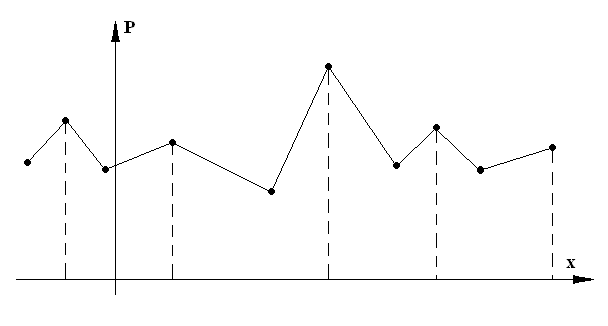
Рисунок 16

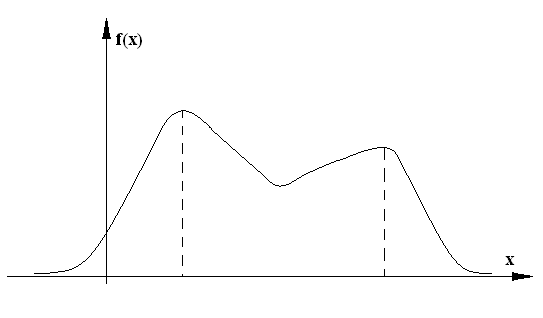
Рисунок 17

Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом.

Такие системы называют антимодельными.

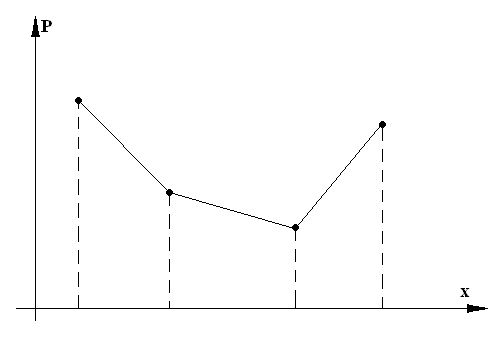
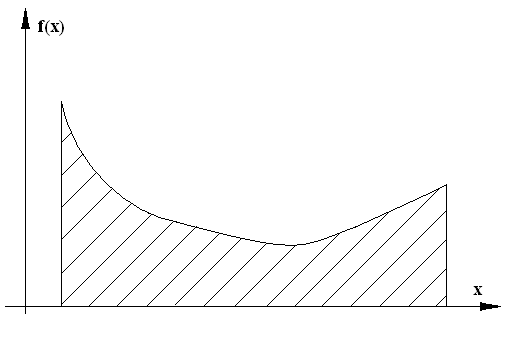
Рисунок 18 Рисунок 19

Часто применяется еще одна характеристика положения – медиана случайной величины.

Этой характеристикой обычно пользуются для поправочных случайных величин.

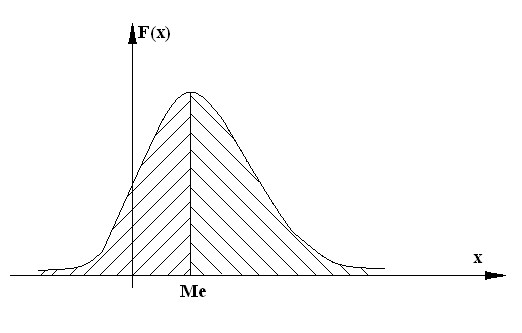
Рисунок 20 – медиана случайной величины

Медианой случайной величины X называется такое ее значение, для которого

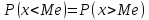
Геометрическая медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

Лекция №8

Показатели надеж ности технических элементов и систем

Показатель надежности – это количественная характеристика одного или нескольких свойств, составляющих надежность объекта.

Различают следующие показатели надежности:

• Единичный показатель надежности

• Комплексный показатель надежности

• Расчетный показатель надежности

• Экспериментальный показатель надежности – это показатель надежности, точная или интервальная оценка которого определяется по данным эксплуотации

• Эксплуатационный показатель надежности

• Экстраполированный показатель надежности

В зависимости от оцениваемых свойств, характеризующих надежность, показатели надежности подразделяют на:

• Показатели безотказности

• Показатели долговечности

• Показатели ремонтопригодности

• Показатели сохраняемости

• … показатели надежности

Показатели безотказности

Для необслуживаемых, невосстанавливаемых и не ремонтируемых объектов в качестве показателей безотказности используют:

• Вероятность безотказности работы

• Интенсивность отказов

• Среднюю наработку до отказа

• Гамма-процентную наработку до отказа

Для обслуживаемых, восстанавливаемых и ремонтируемых объектовв качестве показателей безотказности используют:

• Среднюю наработку на отказ

• Параметр потока отказов

• Усредненный параметр потока отказов

Вероятность безотказной работы – это вероятность того, что в пределах заданной наработки отказ объекта не возникнет.

Обозначим через t время или суммарную наработку объекта. Возникновение первого отказа – случайное событие, а наработка τ от начального момента до возникновения этого события – случайная величина. Вероятность безотказности работы P(t) объекта в интервале наработки от 0 до t включительно определяется как:

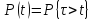
Вероятность безотказности работы связана с функцией распределения F(t) и плотностью f(t) распределения наработки до отказа.

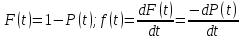
Иногда, наряду с понятием «вероятности безотказной работы» используют понятие «вероятности отказа», Q(t).

Q(t) – вероятность того, что объект откажет хотя бы один таз в течение заданной наработки, будучи работоспособным в начальный момент времени.

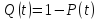
<Используя приведенные выше зависимости, получаем>:

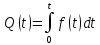
Плотность распределения f(t) наработки до отказа называют частотой отказов. <Типичная зависимость частоты f отказов от наработки t изображена на рисунке1>

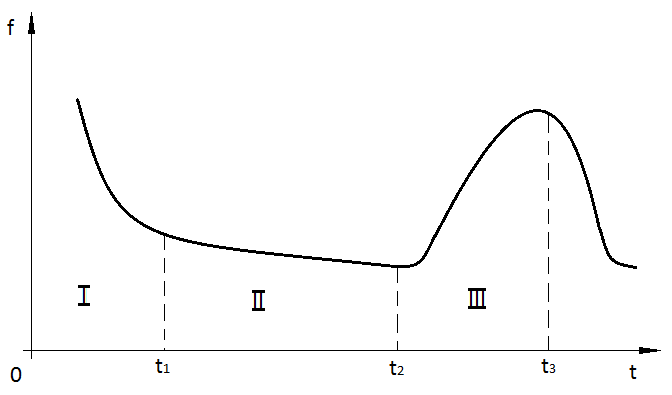
Рисунок 21

<Из рисунка 1 видно, что все время работы изделия можно разделить на три участка, соответствующие трем независимым группам отказов.>

Временной промежуток от 0 до t₁ называется участком приработки. <На этом участке происходят отказы в основном из-за дефектов производства.> На участке от t₁ до t₂ выход из строя изделия в основном обусловлен внезапным отказом. Временной промежуток от t₂ до t₃ характеризуется возрастанием частоты отказов из-за деградационных процессов.

Деградационный отказ – это отказ, обусловленный естественными процессами старения, изнашивания, коррозией и усталостью, при соблюдении всех установленных правил и (или) норм проектирования, изготовления и эксплуотации.

Точечные статистические оценки для вероятности безотказной работы P_стат(t), вероятности отказов Q_стат(t) и частоты отказов f_стат(t) определяются как:

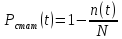
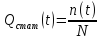
Где:

N – число объектов, работоспособных в начальный момент времени;

Δt – промежуток времени (наработки);

n(Δt) – число объектов, отказавших в интервале времени (наработки) от 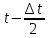до ;

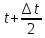n(t) – число объектов, отказавших на отрезке от 0 до t.

Интенсивность отказов λ(t) – это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник.

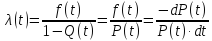
Преобразуем это выражение для того, чтобы выразить P(t) через λ(t)

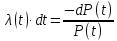
Интегрируя обе части выражения от 0 до t получаем

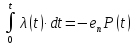
Откуда

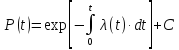
Используя начальные условия t=0 и P(0)=1 найдем C=0. <зависимость вероятности безотказной работы через λ(t) будет иметь вид>

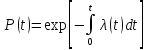
Статистическая оценка для интенсивности отказов имеет вид:

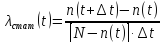
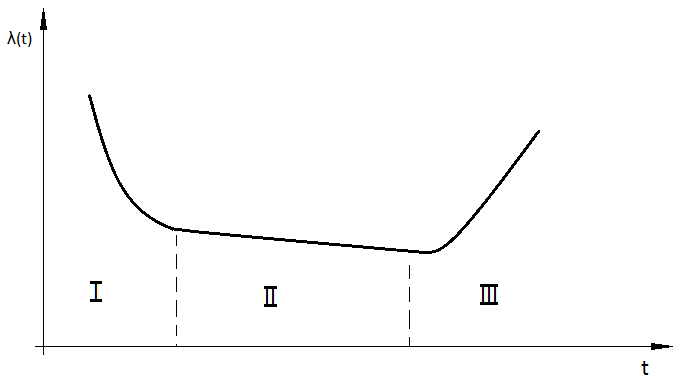
Рисунок 22- Типичная зависимость интенсивности отказов от времени.

Для участка II, на котором изделие работает наиболее долго, зависимость вероятности безотказной работы от времени имеет вид:

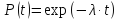
- экспоненциальный закон вероятности безотказной работы

Средняя наработка до отказа (T₁) – это математическое ожидание наработки объекта до первого отказа. Она определяется по формуле:

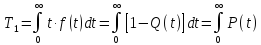
Для второго участка работы (рисунок 2), когда интенсивность отказов λ не зависит от времени t, средняя наработка отказа равна:

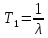
Среднее время безотказной работы в интервале от 0 до t, при экспоненциальном законе вероятности безотказной работы:

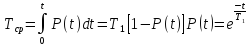
Дисперсия времени безотказной работы:

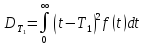
Среднее квадратичное отклонение:

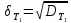
Статистическую оценку средней наработки до отказа T_стат вычисляют по формуле:

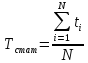
Гед:

N – число отказов, произошедших за наработку t

t_i – наработка отказа i-го элемента.

Гамма – процентная наработка до отказа – это наработка t_ɣ, в течение которой отказ не возникает с вероятностью ɣ, выраженной в прорцентах

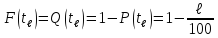
где: F(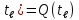 - функция распределения наработки до отказа

P(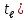 – вероятность безотказной работ.

Лекция №9