
- •Содержание
- •Введение
- •Тема 1. Элементы теории множеств
- •1.1. Понятие множества, способы задания множеств
- •Множества
- •1) Перечисление элементов.
- •2) Указание характеристического свойства.
- •1.2. Примеры решения задач
- •Тема 2. Элементы линейной алгебры
- •2.1. Понятие матрицы, операции над матрицами
- •2.2. Примеры решения задач
- •Тема 3. Элементы векторной алгебры
- •3.1. Векторы на плоскости
- •3.2. Примеры решения задач
- •Тема 4. Дифференциальное исчисление
- •4.1. Понятие производной функции
- •4.2. Примеры решения задач
- •Тема 5. Интегральное исчисление
- •5.1. Первообразная и неопределенный интеграл
- •5.2. Примеры решения задач
- •Тема 6. Элементы теории вероятностЕй
- •6.1. Понятие вероятности случайного события
- •6.2. Примеры решения задач
- •Тема 7. Элементы математической статистики
- •7.1. Основные понятия
- •7.2. Примеры решения задач
- •Контрольные задания
- •Денотатный граф
- •Блок-схема по методу Штейнберга
- •Дифференциальные уравнения. Дифференциальные уравнения первого порядка с разделяющимися переменными.
3.2. Примеры решения задач
Задача
1. Найти длины
и скалярное
произведение векторов
![]() ,
,
![]() ,
если известно
,
если известно
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
угол между векторами
,
угол между векторами
![]() .
.
Решение:
![]() .
Тогда
.
Тогда
![]() .
.
Аналогично
![]() .
.
Длина
вектора
![]()
Аналогично
![]() .
.
Скалярное произведение векторов:
![]()
![]() (
(![]() ).
Ответ:
).
Ответ:
![]()
Тема 4. Дифференциальное исчисление
4.1. Понятие производной функции
Определение1: Производной функции f(x) в точке х0 называется предел (если он существует) отношения приращения функции ∆ f в этой точке к приращению аргумента ∆х, когда последнее стремится к нулю:
![]()
Обозначается
![]() или
или
![]()
Нахождение производной функции называется дифференцированием.
Определение2:
Дифференциалом
функции f(x)
называется
произведение производной этой функции
![]() на
произвольное приращение аргумента.
на
произвольное приращение аргумента.
Обозначается
![]() или
или
![]() ,
где
,
где
![]() .
.
Основные правила дифференцирования
1. Производная постоянной
Символьная
формулировка:
![]()
Словесная формулировка: производная постоянной равна нулю.
2. Производная алгебраической суммы функций
Символьная
формулировка:
![]()
Словесная формулировка: производная алгебраической суммы функций равна сумме производных этих функций.
3. Производная произведения двух функций
Символьная
формулировка
![]()
Словесная формулировка: производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго.
4. Производная произведения постоянной на функцию:
Символьная
формулировка
![]()
Словесная формулировка: Постоянный множитель можно выносить за знак производной.
5. Производная частного двух функций:
Символьная
формулировка:
![]()
6. Производная сложной функции:
Пусть
y
есть функция от u:
![]() а переменная u,
в свою очередь, есть функция от аргумента
х:
а переменная u,
в свою очередь, есть функция от аргумента
х:
![]() т.е.
если у
зависит от х
через промежуточный аргумент u,
то у
называется сложной
функцией от
х (функцией
от функции):
т.е.
если у
зависит от х
через промежуточный аргумент u,
то у
называется сложной
функцией от
х (функцией
от функции):
![]()
Символьная
формулировка:
![]()
Словесная формулировка: Производная сложной функции равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной х:
Таблица производных элементарных функций
|
Функция у |
Производная
|
|
С |
0 |
|
х |
1 |
|
для
сложной функции: |
|
|
для
сложной функции:
|
|
|
для
сложной функции:
|
|
|
для
сложной функции:
|
|
|
для
сложной функции:
|
|
|
для
сложной функции:
|
|
|
Функция у |
Производная
|
|
для
сложной функции:
|
|
|
для
сложной функции:
|
|
|
для
сложной функции:
|
|
|
для
сложной функции:
|
|
4.2. Примеры решения задач
Задача 1.
Объем
продукции u
(ед), произведённый бригадой рабочих,
может быть описан уравнением
![]() (ед),
(ед),
![]() ,
где
,
где
![]() -рабочее
время, часы. Вычислить производительность
труда, скорость и темп ее изменения
через час после начала работы и за час
до ее окончания.
-рабочее
время, часы. Вычислить производительность
труда, скорость и темп ее изменения
через час после начала работы и за час
до ее окончания.
Решение.
Производительность
труда выражается производной
![]() .
Используя правило нахождения производной
суммы функций –
.
Используя правило нахождения производной
суммы функций –
![]() ,
получим
,
получим
![]() .
Используя правила нахождения производной
произведения постоянной на функцию:
.
Используя правила нахождения производной
произведения постоянной на функцию:
![]() ,
производной степенной функции
,
производной степенной функции
![]() ,
производной константы:
,
производной константы:![]() имеем:
имеем:
![]()
![]() (ед/ч)
(ед/ч)
Скорость
изменения производительности –
производная
![]() .
Темп изменения производительности –
логарифмическая производная
.
Темп изменения производительности –
логарифмическая производная
![]() (используем правило вычисления производной
сложной функции, где
(используем правило вычисления производной
сложной функции, где
![]() )-
сложная функция).
)-
сложная функция).
Найдем
![]() :
:
![]() (см.
выше правила нахождения производной
функции).
(см.
выше правила нахождения производной
функции).
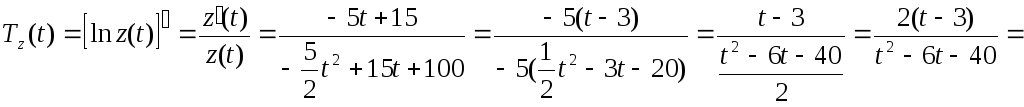
![]() (ед/ч).
(ед/ч).
В
заданные моменты времени
![]() и
и
![]() соответственно
имеем:
соответственно
имеем:
![]() (ед/ч),
(ед/ч),
![]() (ед/ч),
(ед/ч),
![]() ,
,
![]() ,
,
![]() (ед/ч),
(ед/ч),
![]() (ед/ч).
(ед/ч).
Итак,
к концу работы производительность труда
существенно снижается, при этом изменение
знака
![]() и
и
![]() с
плюса на минус свидетельствует о том,
что увеличение производительности
труда в первые часы рабочего дня сменяется
ее снижением в последние часы.
с
плюса на минус свидетельствует о том,
что увеличение производительности
труда в первые часы рабочего дня сменяется
ее снижением в последние часы.
Задача
2. Найти
дифференциал функции
![]()
Решение.
По определению
![]()
![]() (использовали
правило нахождения сложной функции
(использовали
правило нахождения сложной функции
![]() см. таблицу
см. таблицу
![]() =
=![]() ).
).
