Отметим, что Статические уравнения Навье

Из дифференциальных уравнений равновесия внутри тела (3.1) остается два:

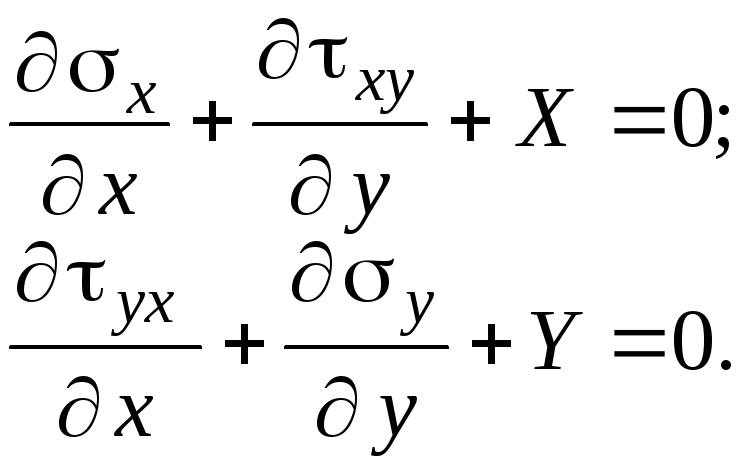(4.9)

Третье уравнение (3.1) обращается в тождество, т. к. входящие в него напряжения имеют следующий вид:

(4.10)

а интенсивность объемных нагрузок, параллельных оси z, равна нулю, т. е. .

Три уравнения равновесия на поверхности тела (3.6), учитывая, что для боковой поверхности и выполняется условие (4.10), превращаются в два условия:

(4.11)

Итак, восемь уравнений (4.4), (4.8), (4.9) содержат восемь неизвестных функций:

Три компоненты деформации выражаются через две функции . Следовательно, они не могут выбираться произвольно и должны удовлетворять уравнениям сплошности деформаций Сен-Венана (3.3). Дважды дифференцируя первое уравнение (4.4) по , а второе – по , а затем складывая их, получим

которое, если учесть третье уравнения (4.4), является одним из шести условий сплошности Сен-Венана

(4.12)

Из шести условий сплошности (неразрывности деформаций) Сен-Венана остаётся только уравнение (4.12), а остальные тождественно удовлетворяются. Для тела, подчиняющегося закону Гука (4.8), это условие можно выразить в напряжениях:

(4.13)

где называется оператором Лапласа или гармоническим оператором.

Если ограничиться исследованиями задач, в которых объемные силы не зависят от координат, то условие сплошности (4.13) упрощается и принимает вид:

(4.14)

Таким образом, для трех компонент напряжений при плоской деформации в случае объемных нагрузках имеем три уравнения:

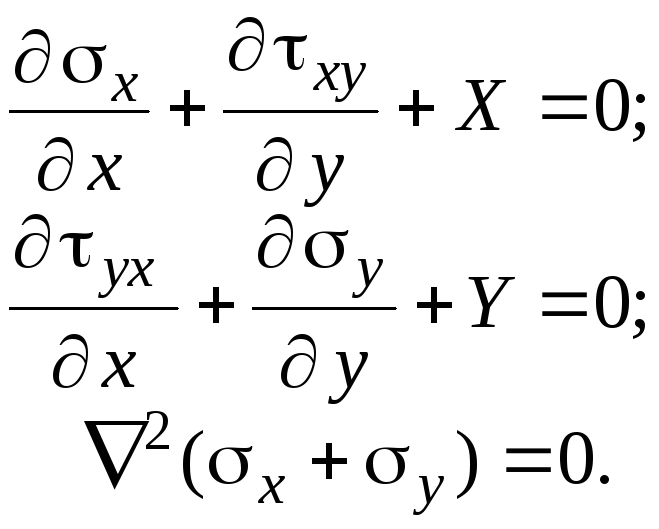(4.15)

Для цилиндрического тела большой длины, к которому приложены нагрузки (4.1) и (4.2), решение задачи о плоской деформации имеет значение даже и в том случае, если концы стержня будут перемещаться в направлении оси .

Действительно, если определены напряжения в сечениях стержня при , то можно определить главный вектор и главный момент внешних сил, приложенных к торцам. Теперь наложим на решение, соответствующее плоской деформации, решение задачи методами сопротивления материалов под действием сил, равных по величине и противоположных по направлению главному вектору и главному моменту сил, возникающих при плоской деформации, на торцах.

Очевидно, что при этом получаем решение задачи о напряжениях в теле, к которому приложены нагрузки по боковой поверхности (4.1) и по объему (4.2), а на торцах нагрузки статически эквивалентны нулю. Согласно принципу Сен-Венана для достаточно длинного тела на участках, удаленных от торцов, полученное решение будет справедливо и в том случае, если торцы тела будут свободны и от закреплений, и от нагрузок.

4.2. Плоское напряженное состояние

Р

Рис. 17

ассмотрим другой предельный случай, когда размер тела в направлении оси мал по сравнению с размерами по осям и . Например, тонкая пластинка постоянной толщины нагружена силами, приложенными по контуру пластинки параллельно ее срединной плоскости и распределенными равномерно по ее толщине (рис. 17). Пусть – наименьший размер пластинки и .

Тогда, как и в случае плоской деформации, возможно упрощение основных уравнений теории упругости.

Поскольку поверхностные нагрузки по боковым плоскостям отсутствуют, то и компоненты напряжения по этим поверхностям пластинки также равны нулю.

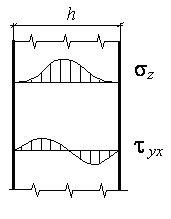
Примечание. На рис. 18 показано эпюры для напряжений и по толщине при точном решении задачи. Кроме того, должно существовать изменение напряжений по координате . Однако, как отмечает С. П. Тимошенко, «в достаточно тонкой пластинке им можно пренебречь подобно тому, как пренебрегают существованием мениска на вершине столбика жидкости в капиллярной трубке термометра» [2]. Поэтому при малой толщине пластинки принимают:

Рис. 18

(4.16)

т. е. они равны нулю и внутри пластинки. Тогда остальные компоненты напряжения также будут функциями только координат :

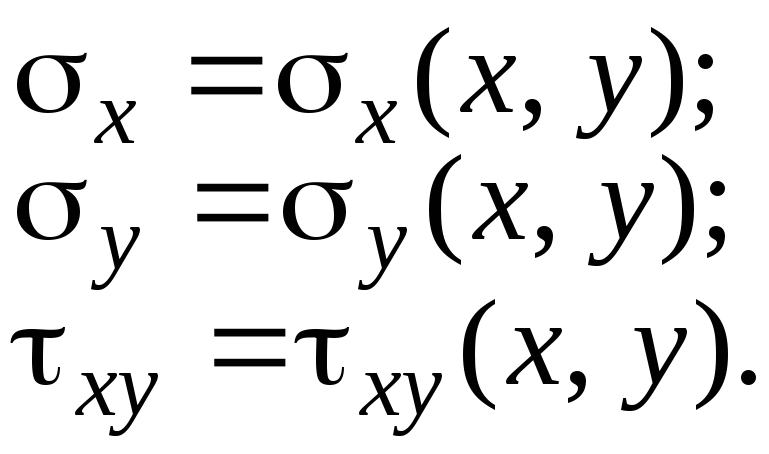(4.17)

На основании (4.16) напряженное состояние пластинки, которое определяется только напряжениями , называется плоским напряженным состоянием.

Рассмотрим общие уравнения теории упругости в случае плоского напряжённого состояния, полагая, что поверхностные и объемные нагрузки определяются, как и при плоской деформации, соотношениями (4.1) и (4.2)

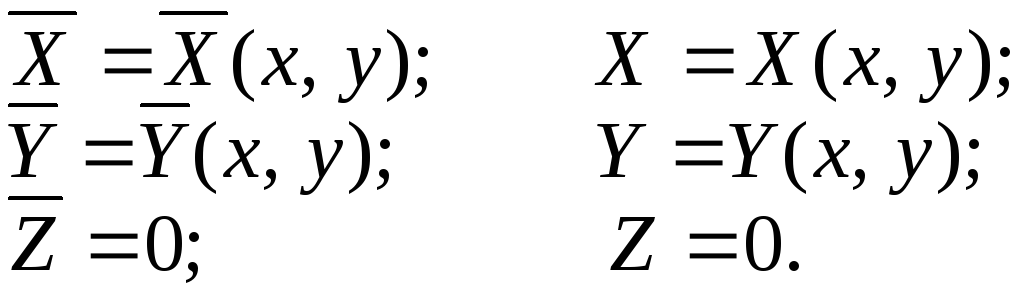(4.18)

Из трех дифференциальных уравнений равновесия для плоского напряжённого состояния остаются только два, которые полностью совпадают с аналогичными уравнениями (4.9):

(4.19)

Напряжения непрерывно изменяются по объему рассматриваемой пластинки, Уравнения (4.19) должны удовлетворяться во всех точках по объему нагруженного тела. При достижении его границ напряжения должны быть такими, чтобы находиться в равновесии с поверхностными нагрузками, приложенными на границе пластинки. Поэтому внешние нагрузки можно рассматривать как продолжение внутренних сил. Условия равновесия на поверхности имеют вид (3.6). Из трех уравнений (3.6) останутся только два:

(4.20)

После введенных допущений закон Гука примет вид

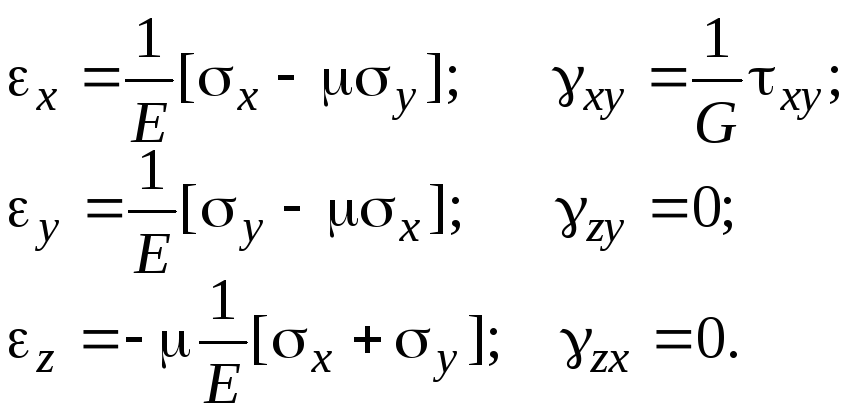(4.21)

Как видно, функции деформаций зависят только от координат . Из шести уравнений Коши (3.2) для плоского напряжённого состояния останутся только три уравнения

(4.22)

совпадающие с уравнениями (4.4).

Три компоненты деформаций выражаются через две функции и . Поэтому деформации не могут задаваться независимо друг от друга. Дважды дифференцируя первое уравнение (4.22) по , а второе – по , а затем их складывая, получим

которое, если учесть третье уравнения (4.22), совпадает с одним из шести условий сплошности Сен-Венана (3.3)

(4.23)

Таким образом, как и в случае плоской деформации, имеем восемь неизвестных

Если исключить из уравнения (4.23) компоненты деформации , используя уравнения (4.17) и (4.22), то получим уравнение, совпадающее с (4.13),

При постоянных объемных нагрузках для компонентов напряжения получим систему уравнений

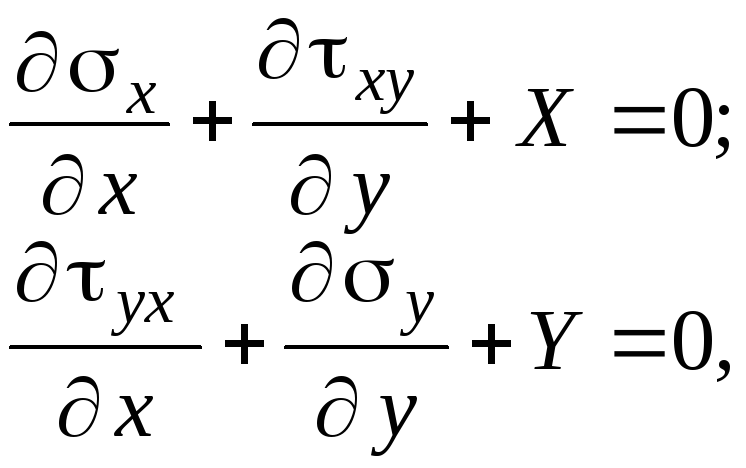(4.24а)

(4.24б)

которая аналогична системе уравнений (4.15) для плоской деформации.

На поверхности тела компоненты напряжения должны удовлетворять статическим граничным условиям (4.20).