
- •1.1.1. Полное, нормальное и касательные напряжения на наклонной площадке
- •1.1.2. Вычисление проекции касательного напряжения на заданное направление
- •1.1.3. Главные напряжения, определение положения главных площадок
- •1.2. Деформированное состояние в точке тела
- •1.2.1. Определение линейной, угловой и объёмной деформаций
- •2. Задача 2 “Постановка кинематических и статических граничных условий”
- •3. Задача 3 "Обратный метод решения задач в теории упругости. Определение нагрузок, приложенных к телу"
- •3.1. Основные уравнения теории упругости
- •3.2. Пример решения задачи
- •3.2.1. Постановка задачи
- •3.2.2. Определение компонентов деформаций
- •3.2.3. Определение компонент напряжений
- •3.2.4. Определение объемных нагрузок
- •3.2.5. Определение поверхностных нагрузок
- •3.2.6. Выводы
- •4. Задача 4 «Плоская задача теории упругости. Функция напряжений»
- •4.1. Плоская деформация
- •Геометрические уравнения Коши
- •Физические уравнения – закон Гука
- •Отметим, что Статические уравнения Навье
- •4.2. Плоское напряженное состояние
- •4.3. Функция напряжений
- •4.4. Изгиб прямоугольной полосы под действием поверхностной нагрузки
- •4.4.1. Постановка задачи
- •4.4.2. Решение задачи
- •4.4.3. Решение задачи методами сопротивления материалов
- •4.4.4. Анализ полученных решений
- •4.5. Изгиб прямоугольной полосы под действием собственного веса
- •4.5.1. Постановка задачи
- •4.5.2. Решение задачи
- •4.5.3 Решение задачи методами сопротивления материалов
- •4.5.4. Анализ полученных решений
3.2.6. Выводы
1. Из рисунка 14
видно, что перемещения
![]() (3.7) вызваны сжатием стержня продольными
внешними нагрузками, равномерно
распределенными по торцам.
(3.7) вызваны сжатием стержня продольными
внешними нагрузками, равномерно
распределенными по торцам.
2. Перемещения
(3.7) обращаются в ноль при
![]() Следовательно, стержень закреплен от
перемещений как абсолютно твердого
тела только в точке пересечения левого
торца с осью стержня.
Следовательно, стержень закреплен от
перемещений как абсолютно твердого
тела только в точке пересечения левого
торца с осью стержня.
4. Задача 4 «Плоская задача теории упругости. Функция напряжений»
При проектировании сооружений возникает большой класс задач, в которых одну из трех прямоугольных координат можно отбросить, и решение задач рассматривать как бы в одной плоскости. Этот класс задач носит название плоской задачи теории упругости. Под плоской задачей теории упругости понимают две различные задачи:
1. Задачу о плоском деформированном состоянии (или о плоской деформации).
2. Задачу о плоском напряженном состоянии.
Обе задачи различны по постановке. Однако если в качестве основных неизвестных выбрать напряжения, то математический аппарат решения обеих задач одинаков. Характерно для этих задач следующее:
1. Число неизвестных равно 3.
2. Все неизвестные являются функциями не трех, а двух координат.
4.1. Плоская деформация
Если при нагружении тела перемещения всех точек в результате деформации происходят только в двух направлениях, т. е. в одной плоскости, то такую деформацию называют плоской.
Рассмотрим стержень
постоянного поперечного сечения, длина
которого в направлении, например, вдоль
оси z
велика
по сравнению с размерами вдоль осей
![]() .
Предположим, что стержень помещен между
гладкими и абсолютно жесткими плоскостями,
и перемещения на торцах вдоль оси
.
Предположим, что стержень помещен между
гладкими и абсолютно жесткими плоскостями,
и перемещения на торцах вдоль оси
![]() отсутствуют (рис. 15). Эффект удаления
этих плоскостей буде рассмотрен ниже.
Объемные и поверхностные нагрузки
перпендикулярны продольной оси
отсутствуют (рис. 15). Эффект удаления
этих плоскостей буде рассмотрен ниже.
Объемные и поверхностные нагрузки
перпендикулярны продольной оси
![]() и не меняется по длине стержня:
и не меняется по длине стержня:
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
Тогда в силу
симметрии нет перемещений
![]() в среднем сечении. То же самое справедливо
для любого сечения. Деформации и
перемещения могут происходить только
в двух направлениях, т. е. только в
плоскости
в среднем сечении. То же самое справедливо
для любого сечения. Деформации и
перемещения могут происходить только
в двух направлениях, т. е. только в
плоскости
![]() возникает
деформация, при которой имеет место
возникает
деформация, при которой имеет место
![]() (4.3)
(4.3)
Рис. 15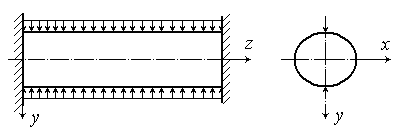
С
Рис. 16
Рассмотрим основные уравнения теории упругости с учетом соотношений (4.1)–(4.3).
Геометрические уравнения Коши
Из уравнений Коши (3.2) видно, что в произвольной точке стержня три компоненты деформации не равны нулю
![]() (4.4)
(4.4)
а остальные три компоненты равны нулю
![]() (4.5)
(4.5)
Вследствие того,
что компоненты перемещений (4.3) не зависят
от переменной z,
то компоненты деформаций (4.4) и напряжений
будут также функциями только двух
переменных
![]() .
.
Физические уравнения – закон Гука
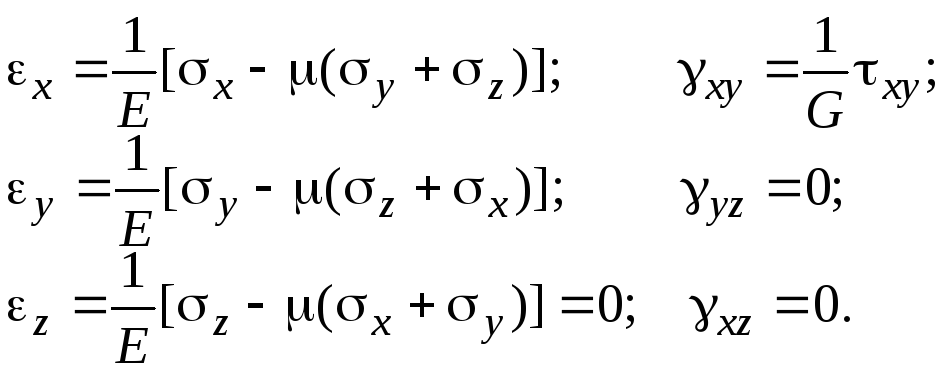 (4.6)
(4.6)
Из третьего
уравнения в первом столбце (4.6) найдем
напряжение
![]()
![]() (4.7)
(4.7)
Исключим
![]() из уравнений (4.6)
из уравнений (4.6)
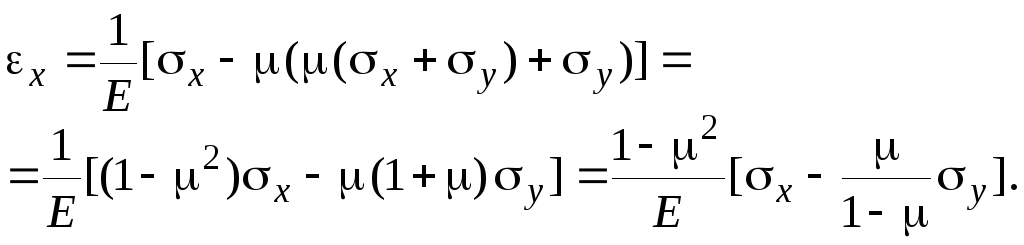
Аналогично
![]()
Примем обозначения
![]()
Тогда
![]()
![]()
![]() (4.8)
(4.8)
