
- •Предел и непрерывность функции одной переменной
- •Введение. Множества и операции над ними
- •Примеры числовых множеств, их стандартные обозначения
- •Пустое множество
- •Включение множеств
- •Равенство множеств
- •Операции над множествами
- •Эквивалентность множеств
- •Мощность множества
- •§ 1. Функция
- •Способы задания функции
- •Аналитический способ задания функции.
- •Табличный способ задания функции.
- •Графический способ задания функции.
- •График функции
- •Обратная функция
- •Основные элементарные функции
- •4) Тригонометрические функции.
- •5) Обратные тригонометрические функции.
- •Суперпозиция функций
- •Классификация функций
- •Задачи к § 1
- •§ 2. Бесконечно малые функции
- •Задачи к §2
- •§ 3. Свойства бесконечно малых функций
- •Задачи к §3
- •§ 4. Бесконечно большие функции
- •Задачи к §4
- •§ 5. Предел функции
- •Односторонние пределы
- •Свойства предела функции
- •Задачи к §5
- •§ 6. Теоремы о вычислении предела функции. Неопределенности
- •Задачи к §6
- •§ 7. Замечательные пределы
- •2) Число . Натуральные логарифмы
- •§ 8. Сравнение бесконечно малых. Эквивалентные бесконечно малые
- •Вычисление пределов степенно-показательных функций
- •Задачи к §8
- •§ 9. Непрерывность функции
- •Второе определение непрерывности
- •Точки разрыва
- •Свойства функций, непрерывных на замкнутом промежутке
- •Задачи к §9
- •Литература
- •Оглавление
Задачи к § 1
Задача 1. Найти
области (![]() )
определения функций:
)
определения функций:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
Указание.
Опираясь на известные области определения
основных элементарных функций, участвующих
в формуле, следует указать те значения
аргумента
![]() ,
для которых определены все действия в
этой формуле.
,
для которых определены все действия в
этой формуле.
Решение.
а) Степенная функция
с показателем степени
![]() определена лишь при неотрицательных
значениях аргумента. Следовательно,
область задания функции определена
неравенством
определена лишь при неотрицательных
значениях аргумента. Следовательно,
область задания функции определена
неравенством
![]() ,
,
решение которого (полученное методом интервалов (рис. 1.15))
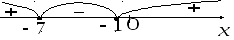
Рис. 1.15.
имеет вид
![]()
Ответ:
![]() .
.
б) Представим функцию в виде
![]() .
.
Результат произведения определен лишь тогда, когда определен каждый из множителей, поэтому область определения задается системой неравенств:
![]()
Решаем ее:
![]()
![]()
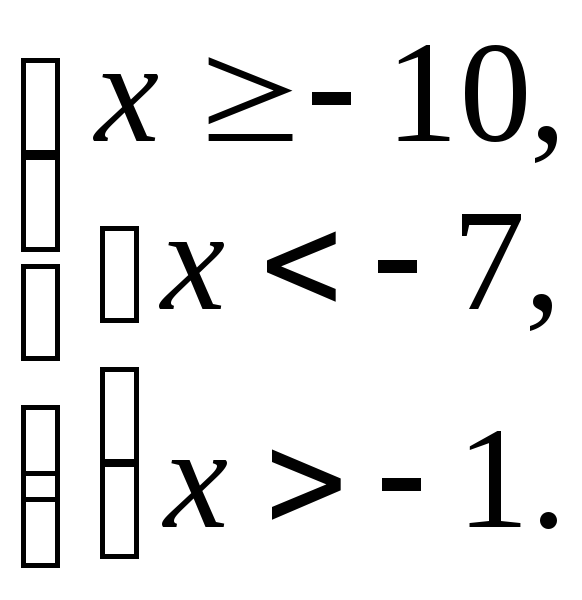
![]()
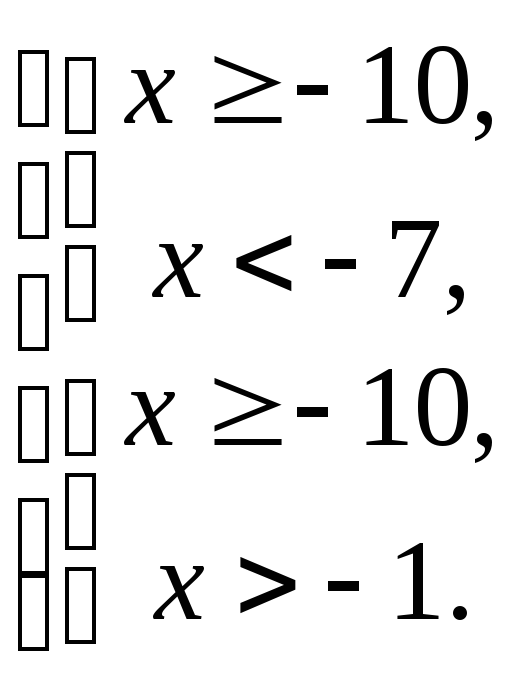
Ответ:
![]() .
.
в) Это – сложная функция, область определения которой задается системой неравенств, описывающих области определения каждой из последовательно вычисляемых функций. Логарифмическая функция определена лишь для положительных значений аргумента, и система неравенств имеет вид:
![]()
Решаем ее:
![]()
![]()
![]()
![]()
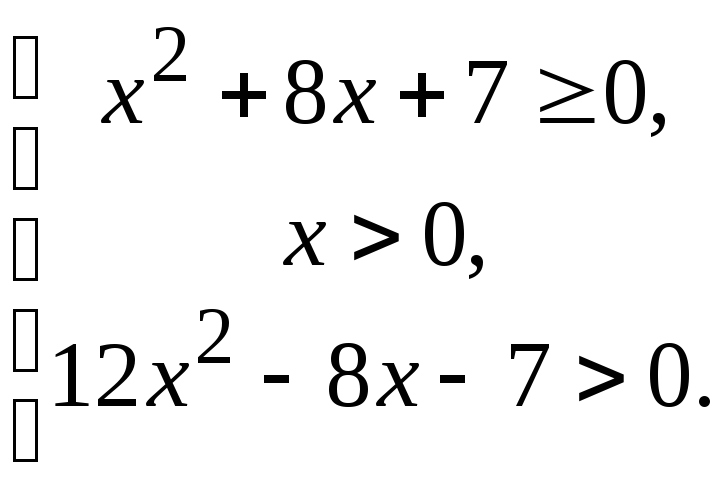
Найдем корни
квадратных трехчленов: уравнение
![]() имеет
корни
имеет
корни
![]() ,
,
![]() ;
уравнение
;
уравнение
![]() имеет корни
имеет корни
![]() ,
,
![]() .
.
Проведем решение системы неравенств методом интервалов (рис.1.16):
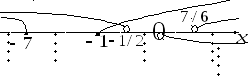
Рис. 1.16.
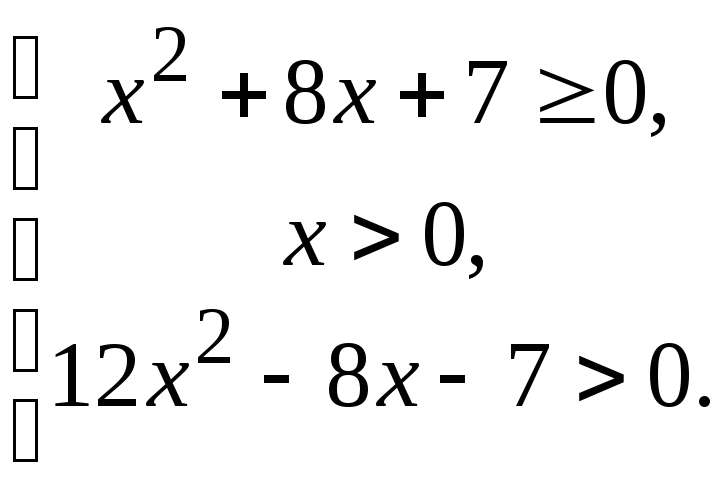
![]()
![]() .
.
Ответ:
![]() .
.
г) Естественная область задания арксинуса определяется двойным неравенством:
![]()
![]()
![]() .
.
Раскрывая входящий в него модуль, будем иметь
![]()
![]()
![]()
![]()
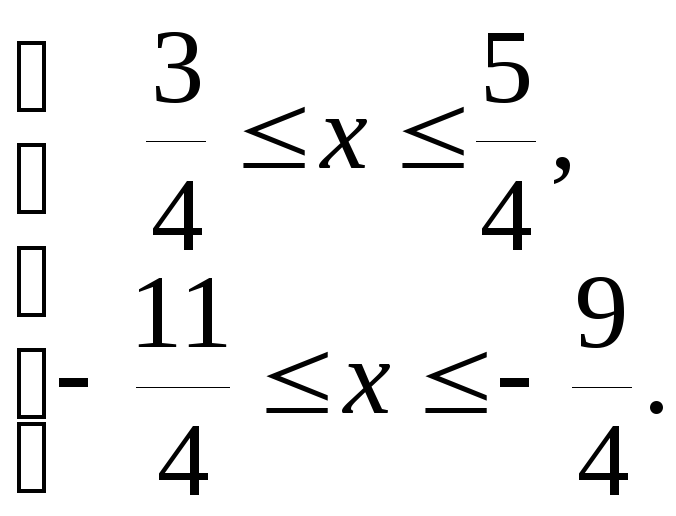
Ответ:
![]() .
.
д) Опираясь на область определения тангенса, составим неравенство:
![]() .
.
Решаем его:
![]() ,
,
![]() .
.
Заметим, что
подкоренное выражение неотрицательно
лишь при
![]() .
.
Ответ:
![]() .
.
Задача 2. Построить графики функций, заданных формулами:
а)
![]()
б)
![]() ;
;
в)

г)
![]() ;
;
д)
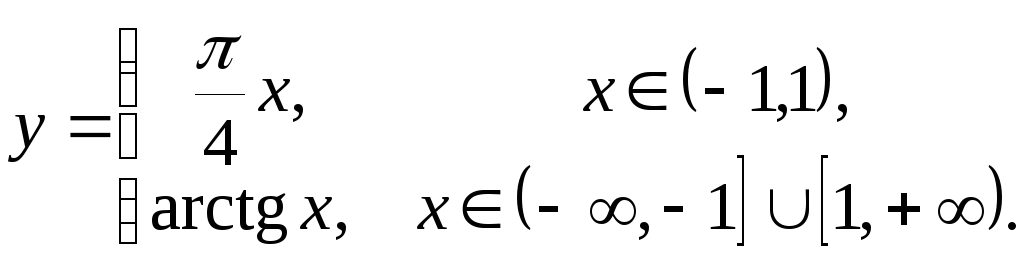
Решение.

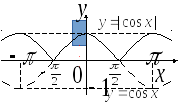 а)
б)
а)
б)
Рис. 1.17. Рис. 1.18.
в
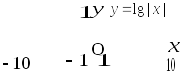 )
г)
)
г)
![]()
Рис. 1.19. Рис. 1.20.
д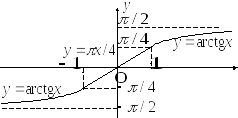 )
)
Рис. 1.21.
В примерах а), в) и д) функции заданы разными формулами на разных интервалах изменения аргумента. На каждом из указанных интервалов строится график заданной на нем основной элементарной функции. Эти графики приведены на рис. 1.17, 1.19 и 1.21 соответственно.
При построении графика для примера б) на рис.1.18, учтено определение модуля, согласно которому
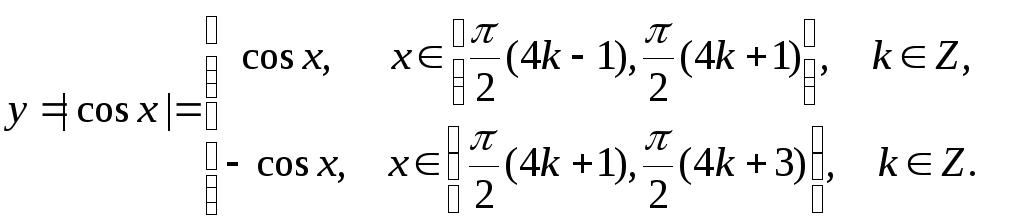
График
![]() показан на рис. 1.18 пунктиром.
показан на рис. 1.18 пунктиром.
В примере г) функция
![]() определена при всех
определена при всех
![]() .
В силу определения модуля она имеет вид
.
В силу определения модуля она имеет вид
![]()
Соответствующий график приведен на рис. 1.20.
Задача 3. Построить графики функций, обратных функциям:
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ;
;
в)
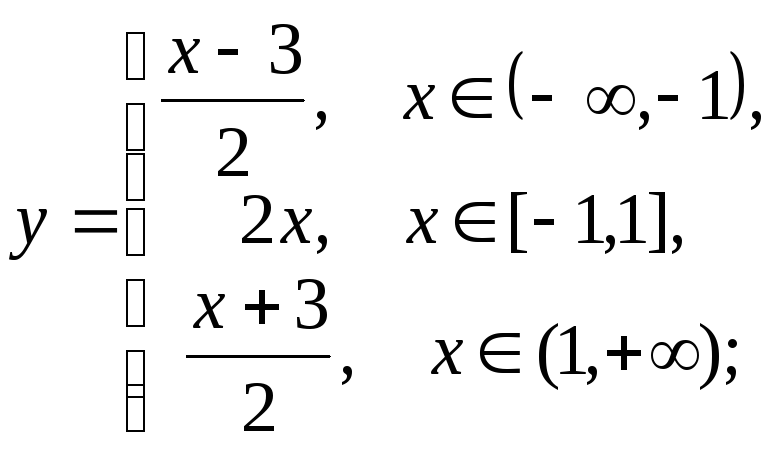
г)
![]() ;
;
д)
![]() ,
,
![]() .
.
Решение.
При построении графика функции, обратной данной, будем пользоваться свойством симметрии графиков взаимно обратных функций относительно биссектрисы первого и третьего координатных углов. Поэтому на рисунках 1.22 – 1.26 приведены графики заданных функций (показаны жирными пунктирными линиями), обратных к ним функций (показаны жирными сплошными линиями) и график биссектрисы I и III координатных углов (показан тонкой сплошной линией).
а )
б)
)
б)
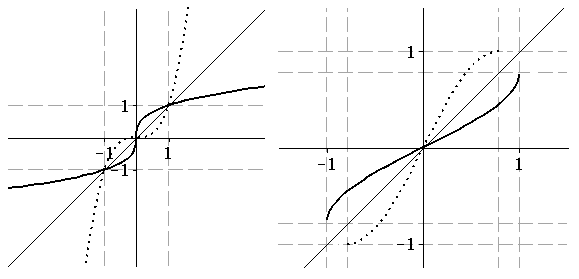
Рис. 1.22. Рис. 1.23.
в )
)
Рис. 1.24.
Поясним иллюстрацию к задаче 3 в). В этой задаче обратная функция имеет вид:

г) д)
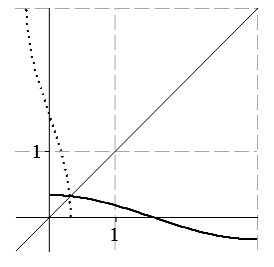
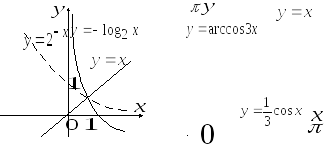
Рис. 1.25. Рис. 1.26.
Задача 4. Представить сложную функцию в виде цепочки, составленной из основных элементарных функций:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
Решение.
Определим
последовательность действий, выполняемых
для вычисления значения функции при
определенном значении
![]() .
.
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() ,
,
![]() ;
;
г)
![]() ,
,
![]() ,
,
![]() ;
;
д)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
