Задачи к §5
Задача 1. Следуя определению предела функции, доказать, что
а)
;
б)
.
Указание.
В окрестности рассматриваемой точки
функцию следует представить в виде:
,
где
– бесконечно малая.
Решение.
а)
.
В окрестности рассматриваемой точки
функции
и
являются бесконечно малыми (см. замечание
2.3), по теореме 3.3 произведение
является бесконечно малой, по теореме
3.1 сумма двух бесконечно малых
– бесконечно малая. Таким образом,
и утверждение доказано.
б) Рассмотрим
разность
и преобразуем ее
.
Функция
является бесконечно малой в точке
.
При
справедливы неравенства
,
поэтому функция
является локально ограниченной при
.
По теореме 3.3 произведение
является бесконечно малой функцией в
точке
.
Следовательно, в окрестности рассматриваемой
точки
,
где
– бесконечно малая.
Задача 2. Задана функция
.
Доказать, что
,
.
Решение.
Согласно замечанию 2.3 функция
является бесконечно малой в точке
,
следовательно, по теореме 5.1
.
Для функции
,
как в примерах 1 а) и б), составим разность
.
Поскольку
при
,
то можно утверждать, что
– бесконечно малая при
.
Следовательно,
.
§ 6. Теоремы о вычислении предела функции. Неопределенности
Из определения 5.1 предела функции в точке (в бесконечно удаленной точке) очевидным образом следует, что
,
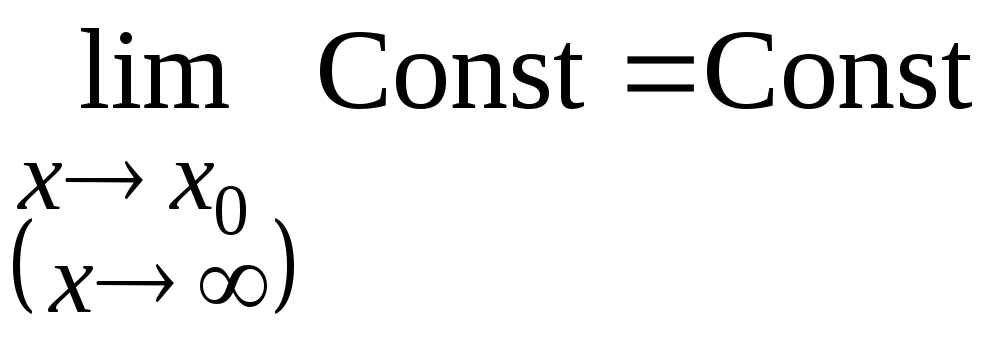а предел бесконечно
малой в точке
(в бесконечно удаленной точке) функции
равен
.
Далее приводятся две теоремы, позволяющие вычислять пределы элементарных функций.
Теорема 6.1.
Пусть
– основная элементарная функция с
множеством задания
и пусть
.
Тогда
.
Замечание 6.1. Теорему следует доказывать для каждой основной элементарной функции отдельно. В рамках данного пособия ее доказательство опускается.
Теорема 6.2. Пусть
функции
и
заданы на множестве
и
,
.
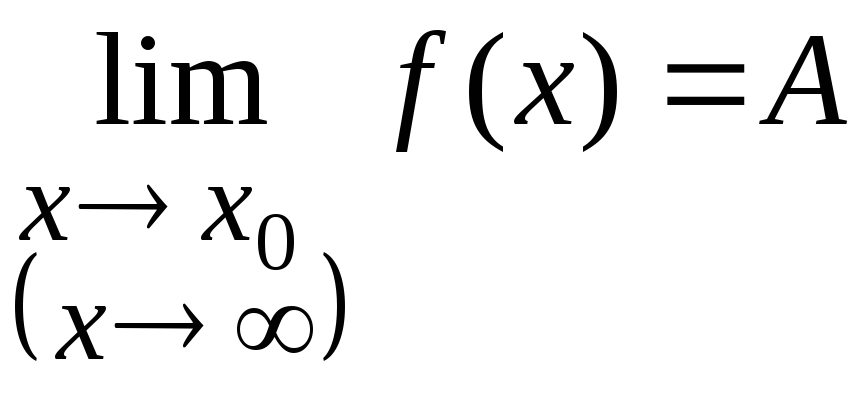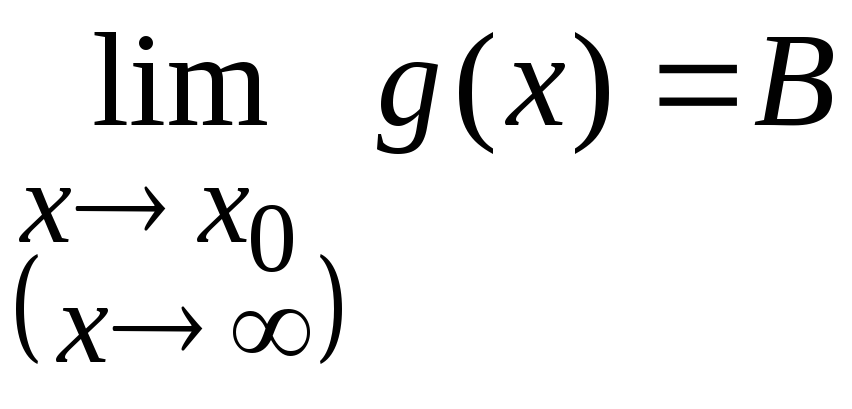Тогда
-
.
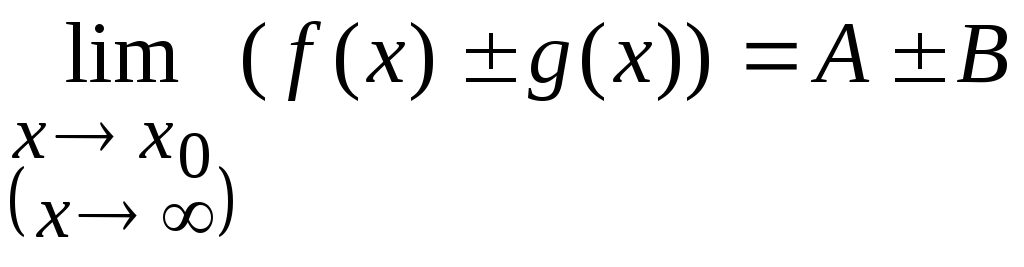2.
.
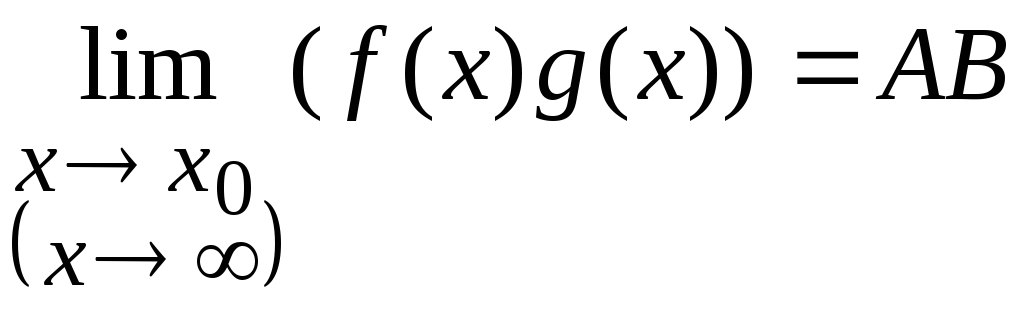3. Если
,
то
.
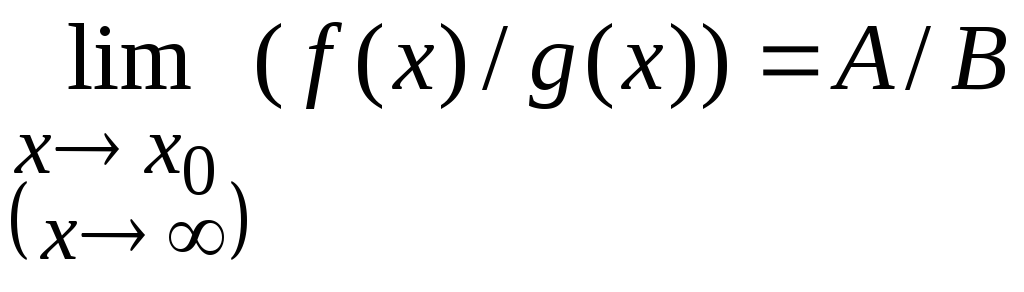Доказательство. Докажем здесь пункты 2. и 3. Пункт 1. читателю предлагается доказать самостоятельно.
2. Согласно определению 5.1 справедливы соотношения
,
,
где
,
– бесконечно малые в точке
(в бесконечно удаленной точке) функции.
Тогда
,
где функция
.
В силу теорем 3.3, 3.4 и следствий 3.1–3.4
функция
является бесконечно малой в точке
(в бесконечно удаленной точке).
Следовательно, по определению 5.1 число
является пределом функции
в точке
(в бесконечно удаленной точке).
3. Используем
представление функций
,
из п. 2. Тогда
.
Числитель дроби
в силу теорем 3.1, 3.2 и 3.3, 3.4 является
бесконечно малой в точке
(в бесконечно удаленной точке) функцией.
Поскольку
– величина бесконечно малая, то для
числа
найдется такое число
(
),
что для всех
(для всех
)
будет выполнено неравенство
.
Далее,
,
откуда
.
Таким образом,
функция
является величиной локально ограниченной
(ограниченной) и в силу теорем 3.3, 3.4
функция
является бесконечно малой в точке
(в бесконечно удаленной точке) функция.
Теорема доказана.
Замечание
6.2. Из п.2
следует, что постоянный множитель можно
выносить за знак предела, т.е., если
–
постоянная, то
.
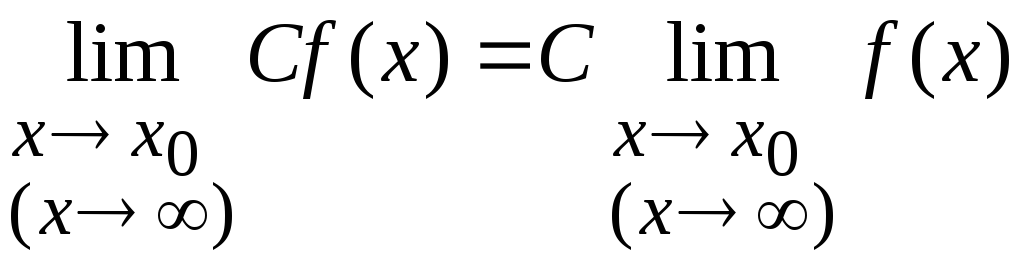Замечание
6.3. Анализируя
текст теорем 6.1 и 6.2, можно прийти к
следующему выводу. Если нужно вычислить
,
где
составлена из основных элементарных
функций и операций сложения, вычитания,
умножения и деления, то можно утверждать,
что
,
если значение
определено (то есть нигде не возникает
деления на нуль, а аргументы всех основных
элементарных функций принадлежат
области их определения).
Пример
6.1. Вычислить
.
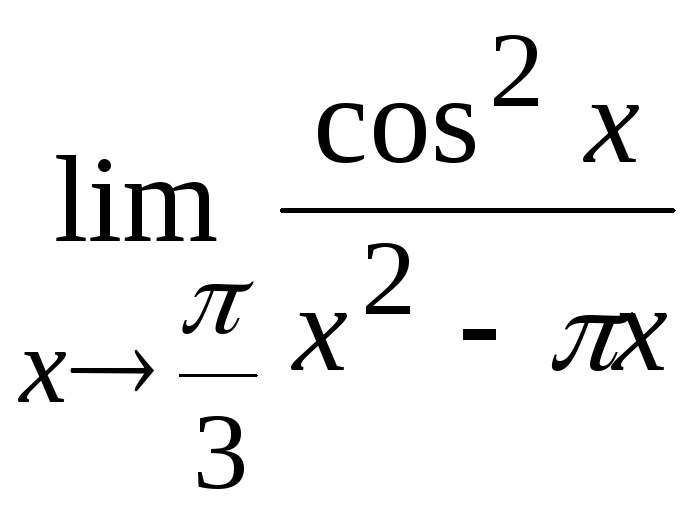Решение. Согласно замечанию 6.3
.
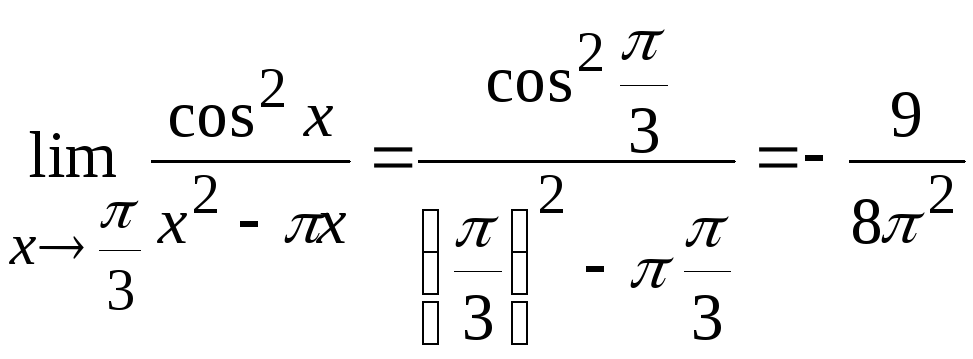Пример
6.2. Вычислить
.
Решение. Согласно замечанию 6.3
.
Однако теорема 6.2 не исчерпывает проблему вычисления пределов элементарных функций. За рамками этой теоремы остались случаи, когда хотя бы один из операндов является бесконечно большим или когда, при определении предела частного предел знаменателя равен нулю.
Часто в этих случаях предел функции можно найти, привлекая теоремы предшествующих разделов или основываясь на определении бесконечно больших и бесконечно малых функций.
Пример
6.3. Вычислить
предел
.
Решение.
Замечая, что
,
а
,
представим выражение в виде
.
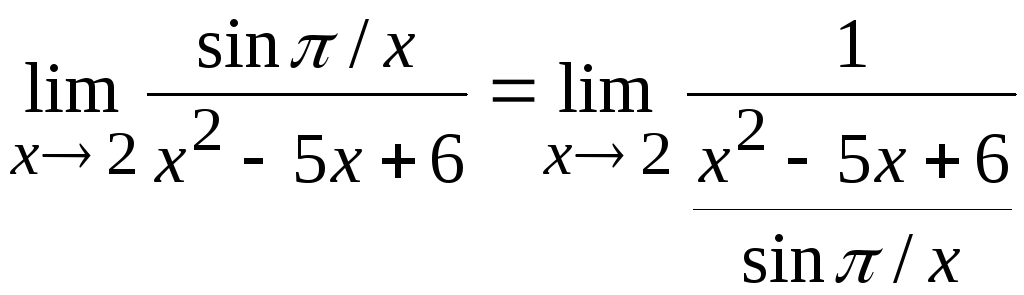По теоремам 6.1, 6.2
,
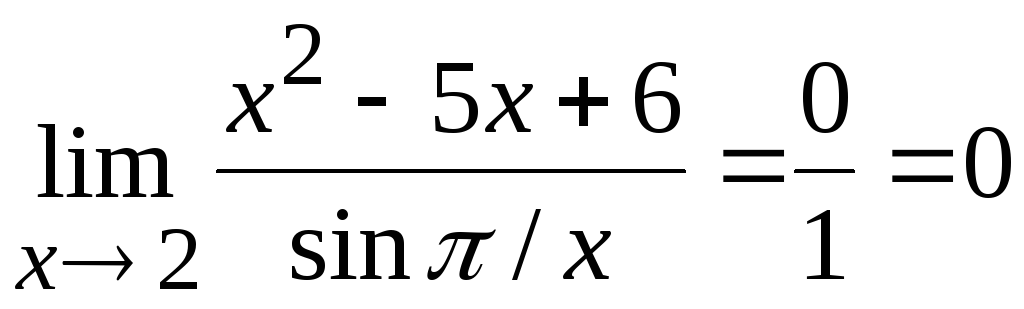то
есть величина
является бесконечно малой в точке
.
Тогда по теореме 4.1 функция
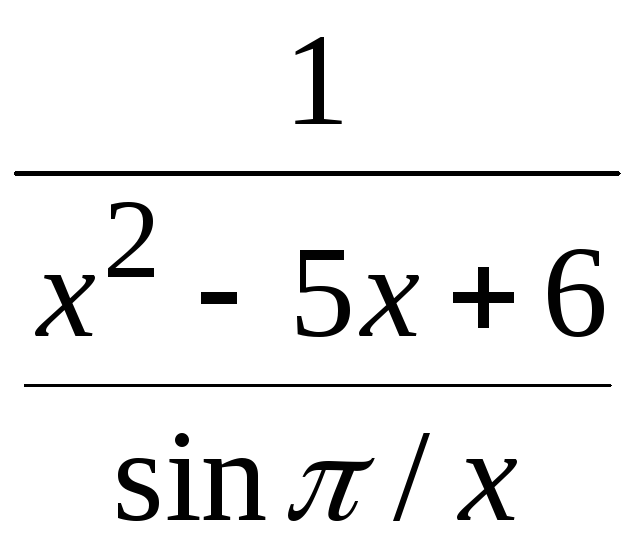является бесконечно большой в точке
.
Таким образом,
.
В приведенном
примере использована теорема 4.1. Напомним
другие полезные утверждения. Так, теорема
4.2 утверждает, что если две бесконечно
большие в какой–либо точке функции
имеют одинаковый знак, то их сумма
является величиной бесконечно большой
в этой точке. В замечании 4.2 указано, что
произведение двух бесконечно больших
в точке
(или бесконечно удаленной точке) функций
является бесконечно большой в этой
точке функцией. В
задаче 2 к §4 показано, что частное
от деления бесконечно большой в точке
функции на функцию, локально ограниченную
в этой точке, является бесконечно большой
функцией. Аналогичное утверждение
справедливо и для бесконечно удаленной
точки.
Однако
в ряде случаев ответ на вопрос о том,
чему равен предел суммы, произведения
или частного операндов, можно получить,
лишь рассмотрев характер стремления
каждого операнда к нулю или бесконечности.
Такие случаи носят название
«неопределенности», а процесс определения
предела в этих случаях – «раскрытием
неопределенности». Неопределенности
имеют специальные обозначения, описывающие
характер операндов и тип операции.
Операции сложения, умножения и деления
приводят к следующим типам неопределенностей:
,
,
,
.
Они читаются так: «бесконечность минус
бесконечность», «нуль умножить на
бесконечность», «нуль делить на нуль»,
«бесконечность делить на бесконечность».
Изложим ряд приемов, используемых при раскрытии перечисленных выше неопределенностей.
I.
Раскрытие
неопределенности типа
,
когда числитель и знаменатель являются
многочленами.
В этом случае следует разложить числитель
и знаменатель на множители и сократить
дробь на общие множители.3
Рассмотрим ряд примеров.
Пример 6.4.
1)
;
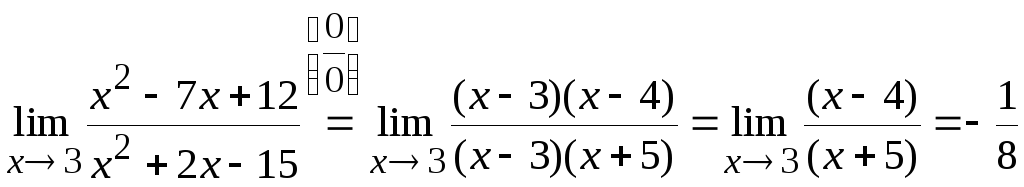2)
;
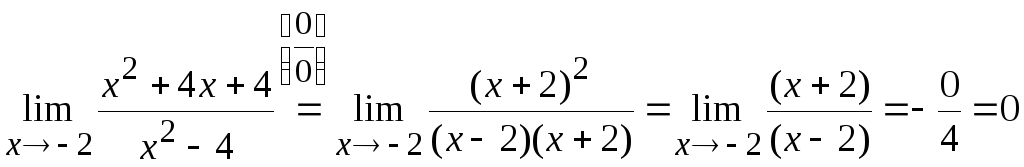3)
.
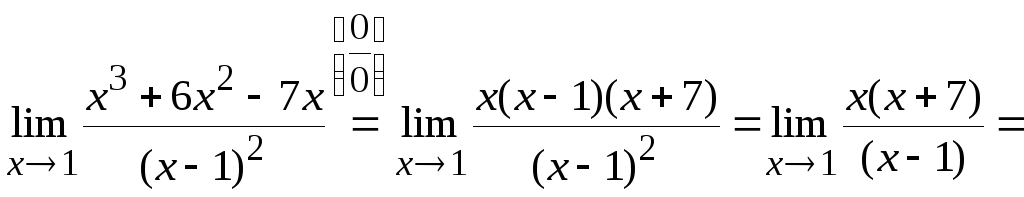
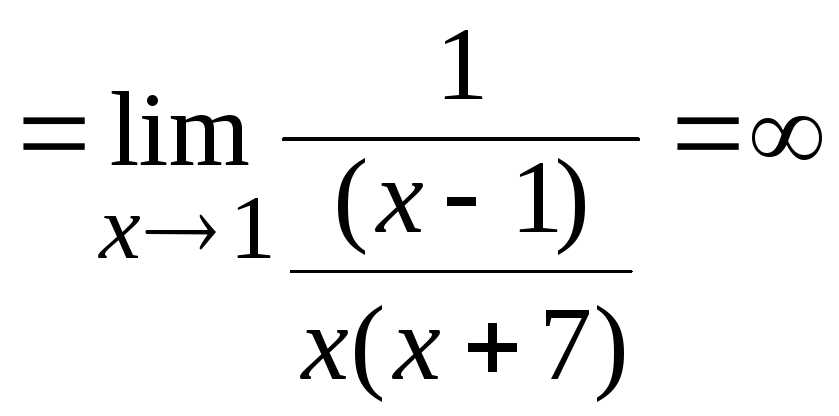II.
Раскрытие
неопределенности типа
,
когда числитель и/или знаменатель
являются иррациональными выражениями.
В этом случае с помощью какого-либо
тождественного преобразования следует
избавиться от иррациональности там,
где она создает неопределенность.
Пример 6.5.
-
Вычислить
.
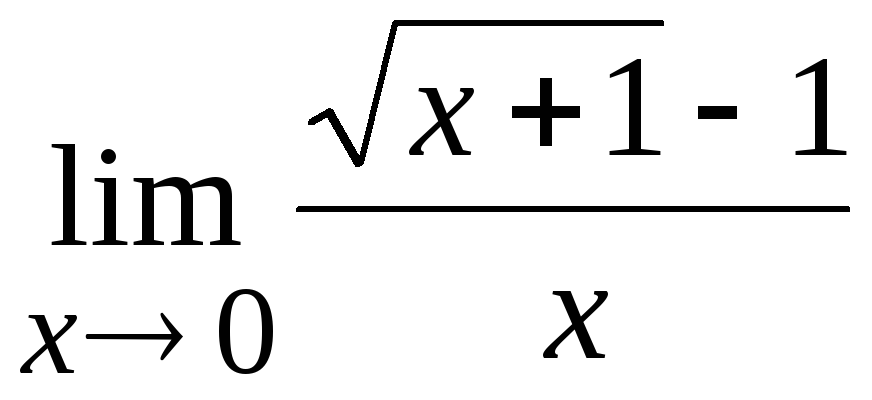Решение.
Имеем неопределенность типа
.
Здесь следует домножить числитель и
знаменатель на выражение
,
являющееся «сопряженным» к
иррациональным выражением. Тогда
иррациональность в числителе исчезнет,
а иррациональность в знаменателе уже
не создаст неопределенности. Получим
.
-
Вычислить
.
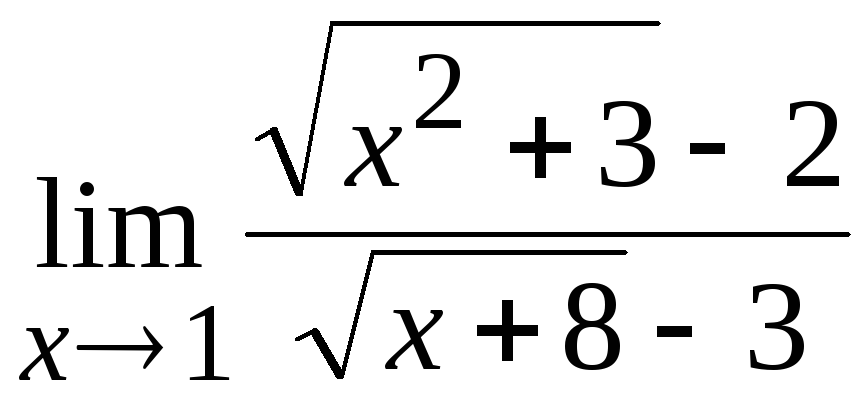Решение.
Имеем неопределенность типа
.
Здесь следует домножить числитель и
знаменатель на два множителя: «сопряженное»
иррациональное выражение к
и «сопряженное» к
.
Получим
.
3)
.
Решение.
Имеем
неопределенность типа
.
Используя формулу разности кубов:
,
следует домножить числитель и знаменатель
дроби на иррациональное выражение,
представляющее собой неполный квадрат
суммы слагаемых, стоящих в числителе.
Получим
.
III.
Раскрытие
неопределенности типа
,
в случае, когда числитель и знаменатель
представляют собой многочлены или
иррациональные выражения.
В этом случае нужно разделить и числитель,
и знаменатель на наивысшую степень
аргумента, содержащуюся в них обоих.
Пример 6.6.
-
Вычислить
.
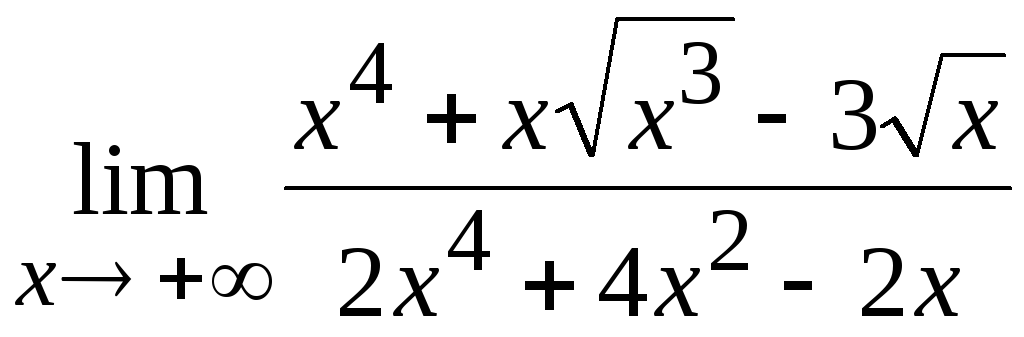Решение.
Очевидно, что числитель и знаменатель
рассматриваемого выражения стремятся
к
,
то есть имеет место неопределенность
типа
.
(Действительно, вынесем
в числителе множитель
за
скобку, будем иметь
.
Поскольку
,
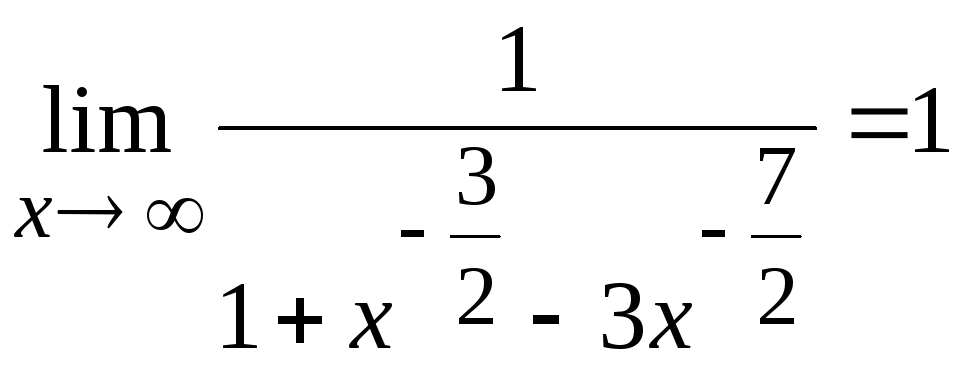по теореме 5.3 функция
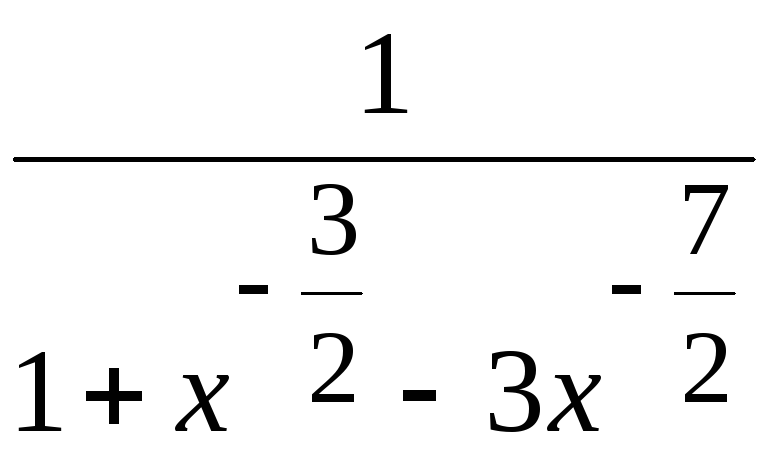ограничена в бесконечно удаленной
точке. Согласно решению задачи 2 к § 4
получим
,
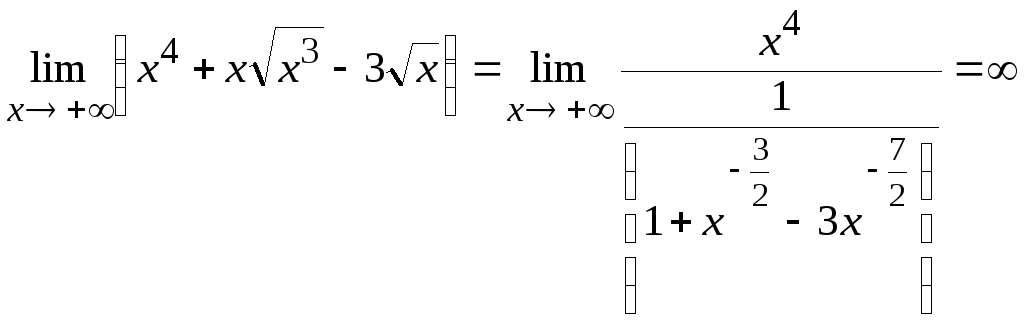как
частное от деления бесконечно большой
при
функции
на ограниченную функцию.
Аналогичный результат получим в знаменателе дроби.)
Вынося в числителе
и знаменателе за скобку множитель
и сокращая числитель и знаменатель на
него, окончательно получим
.
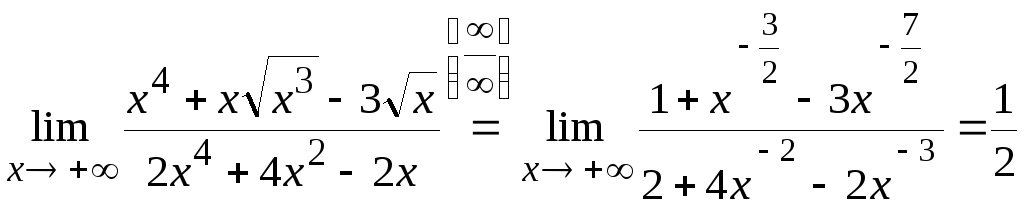2)
Вычислить
.
Решение.
Имеем
неопределенность
.
Вынося в числителе и знаменателе за
скобку множитель
и сокращая на него, получим
.
-
Вычислить
.
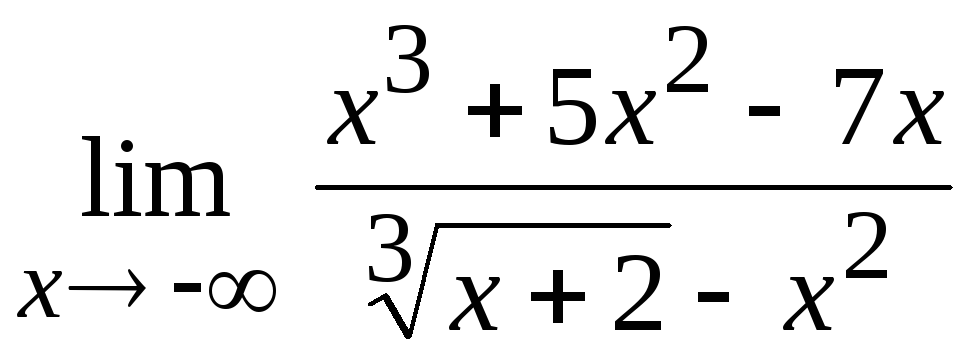Решение.
Имеем неопределенность
.
Вынося в числителе и знаменателе за
скобку множитель
и сокращая на него, получим
Замечание
6.4. На самом
деле нет необходимости скрупулезно
выполнять указанное выше правило. Из
него можно сделать простой вывод. Если
при
высшая степень аргумента в числителе
больше высшей степени аргумента в
знаменателе, то дробь является бесконечно
большой. Если высшая степень аргумента
в числителе меньше высшей степени
аргумента в знаменателе, то дробь
является бесконечно малой. Если высшие
степени аргументов в числителе и
знаменателе равны, то предел дроби равен
отношению коэффициентов при них.
IV.
Раскрытие
неопределенностей вида
или
.
Эти неопределенности следует преобразовать
к виду
или
.
Пример 6.7.
-
Вычислить
.
Решение.
Здесь следует рассмотреть два принципиально
разных случая:
и
.
В первом случае, при
,
имеет место неопределенность вида
.
Для ее раскрытия умножим и разделим
исходное выражение на «сопряженное» к
нему иррациональное выражение. Получим
.
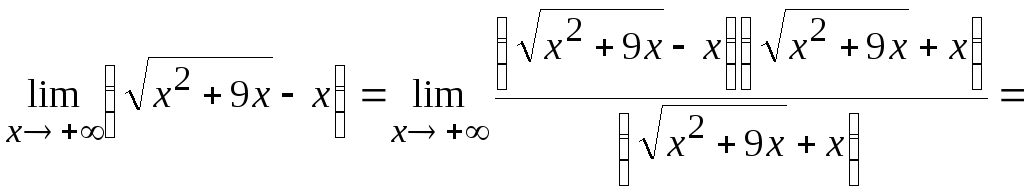
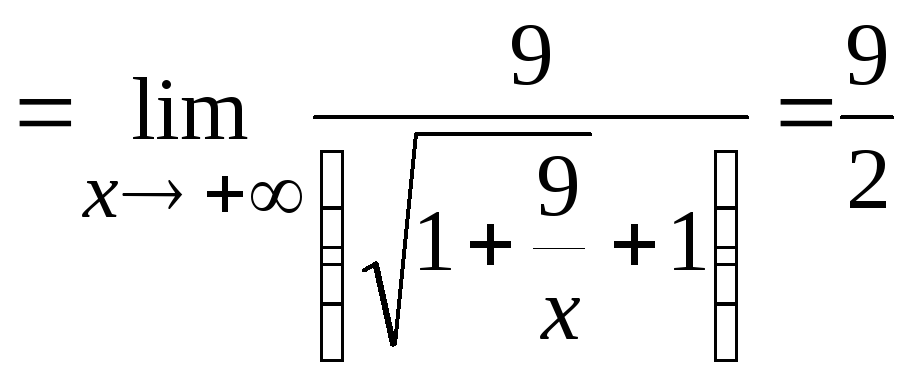Во
втором случае, при
,
под знаком предела оказалась сумма двух
бесконечно больших величин одинакового
знака (неопределенности нет). Тогда
.
Итак,
искомый предел при
не существует, существуют различные
пределы при
и при
:
,
.
2)
Вычислить
.
Решение.
Имеем
неопределенность
.
Для ее раскрытия умножим и разделим
исходное иррациональное выражение на
неполный квадрат суммы. Получим
.
-
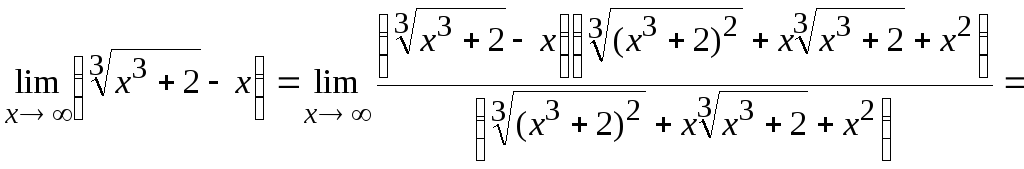
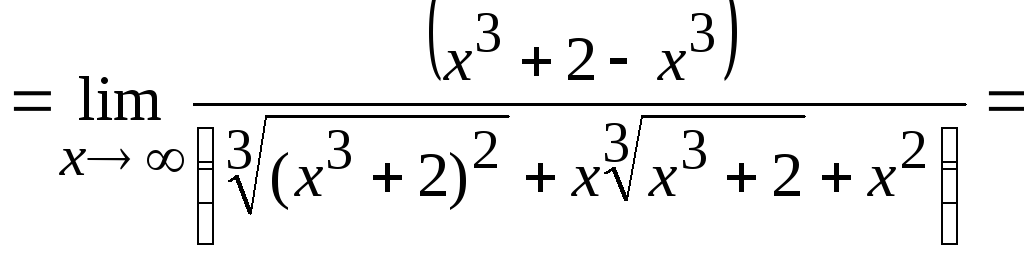
Вычислить
.
Решение.
Имеем неопределенность типа
.
Для ее раскрытия приведем дроби,
составляющие разность, к общему
знаменателю. Получим
.
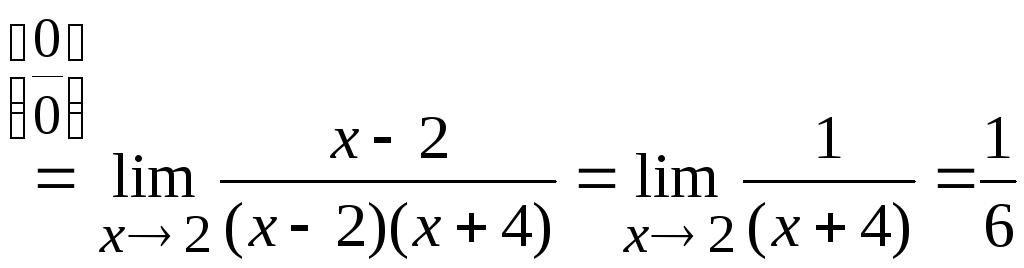