
- •Предел и непрерывность функции одной переменной
- •Введение. Множества и операции над ними
- •Примеры числовых множеств, их стандартные обозначения
- •Пустое множество
- •Включение множеств
- •Равенство множеств
- •Операции над множествами
- •Эквивалентность множеств
- •Мощность множества
- •§ 1. Функция
- •Способы задания функции
- •Аналитический способ задания функции.
- •Табличный способ задания функции.
- •Графический способ задания функции.
- •График функции
- •Обратная функция
- •Основные элементарные функции
- •4) Тригонометрические функции.
- •5) Обратные тригонометрические функции.
- •Суперпозиция функций
- •Классификация функций
- •Задачи к § 1
- •§ 2. Бесконечно малые функции
- •Задачи к §2
- •§ 3. Свойства бесконечно малых функций
- •Задачи к §3
- •§ 4. Бесконечно большие функции
- •Задачи к §4
- •§ 5. Предел функции
- •Односторонние пределы
- •Свойства предела функции
- •Задачи к §5
- •§ 6. Теоремы о вычислении предела функции. Неопределенности
- •Задачи к §6
- •§ 7. Замечательные пределы
- •2) Число . Натуральные логарифмы
- •§ 8. Сравнение бесконечно малых. Эквивалентные бесконечно малые
- •Вычисление пределов степенно-показательных функций
- •Задачи к §8
- •§ 9. Непрерывность функции
- •Второе определение непрерывности
- •Точки разрыва
- •Свойства функций, непрерывных на замкнутом промежутке
- •Задачи к §9
- •Литература
- •Оглавление
Задачи к §6
Задача 1. Найти пределы:
а)
![]() ;
;
б)
![]() ;
;
в)
 ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() ;
;
и)
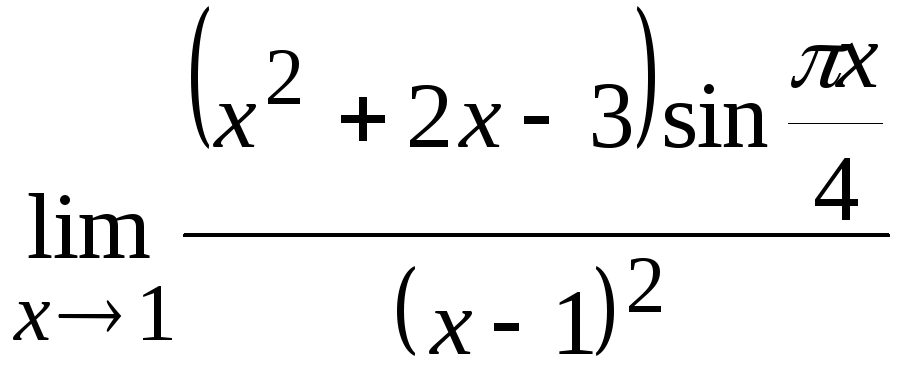 ;
;
к)
![]() ;
;
л)
![]() ;
;
м)
![]() ;
;
н)
![]() ;
;
о)
![]() ;
;
п)
![]() .
.
Указание. При решении примеров а), б), в) следует непосредственно использовать теоремы 6.1 и 6.2.
В примерах г), д) следует использовать определения бесконечно малой и бесконечно большой функций (определения 2.6 и 4.1) и теоремы 3.3, 3.4 и 4.1.
При раскрытии неопределенностей в последующих примерах следует использовать приемы I–IV.
Решение.
а)
![]() .
.
Ответ:
![]() .
.
б)
![]() .
.
Ответ:
![]() .
.
в)

 .
.
Ответ:
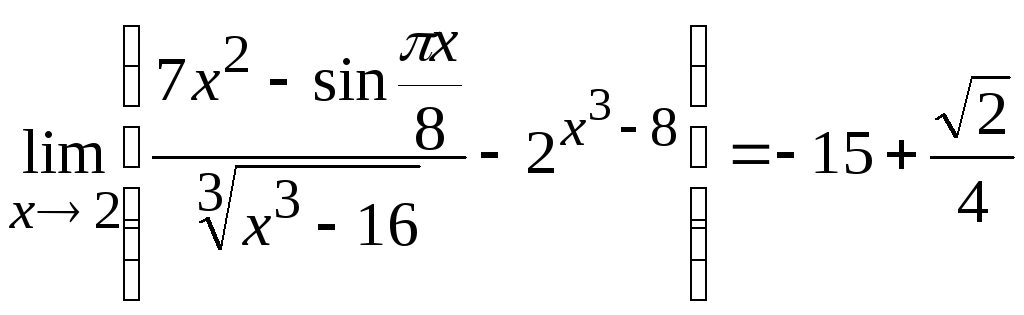 .
.
г)
Величина
![]() при
при
![]() является бесконечно большой:
является бесконечно большой:
![]() ;
;
![]() .
Непосредственно применить здесь теорему
6.1 невозможно. Используем определения
2.6 и 4.1 бесконечно малой и бесконечно
большой функций.
.
Непосредственно применить здесь теорему
6.1 невозможно. Используем определения
2.6 и 4.1 бесконечно малой и бесконечно
большой функций.
Покажем,
что![]() .
Действительно, выбирая произвольное
.
Действительно, выбирая произвольное
![]() ,
укажем для него
,
укажем для него
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
тогда будет выполнено
,
тогда будет выполнено
![]() .
.
Покажем,
что![]() .
Действительно, выберем произвольное
.
Действительно, выберем произвольное
![]() и укажем для него
и укажем для него
![]() (
(![]() ).
Если
).
Если
![]() ,
то
,
то
![]() ,
тогда
,
тогда
![]() .
.
Ответ:
![]() ,
,
![]() .
.
д)
Непосредственно применить теорему 6.2
нельзя, так как по теореме 6.1 получим
![]() .
Поэтому будем использовать теорему
4.1. Поскольку
.
Поэтому будем использовать теорему
4.1. Поскольку
![]() и
и
![]() в окрестности точки
в окрестности точки
![]() ,
будем иметь
,
будем иметь
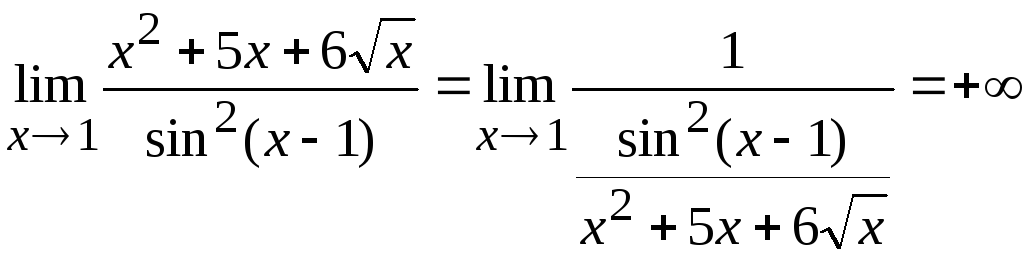 .
.
Ответ:
![]() .
.
е)
Здесь возникает неопределенность типа
![]() .
Воспользуемся правилом, сформулированным
в замечании 6.4, получим
.
Воспользуемся правилом, сформулированным
в замечании 6.4, получим
![]() .
.
Ответ:
![]() .
.
ж)
Имеем неопределенность типа
![]() .
Разделим и числитель, и знаменатель на
.
Разделим и числитель, и знаменатель на
![]() ,
получим:
,
получим:
![]() .
.
Ответ:
![]() .
.
з)
Здесь возникает неопределенность
![]() ,
так как
,
так как
![]() ,
,
![]() .
Для ее раскрытия разложим числитель и
знаменатель на множители и сократим их
на общий множитель:
.
Для ее раскрытия разложим числитель и
знаменатель на множители и сократим их
на общий множитель:
![]() .
.
Ответ:
![]() .
.
и)
Имеем неопределенность типа
![]() .
Разложим числитель и знаменатель на
множители, сократим их на общий множитель
и воспользуемся теоремой 4.1. Получим
.
Разложим числитель и знаменатель на
множители, сократим их на общий множитель
и воспользуемся теоремой 4.1. Получим

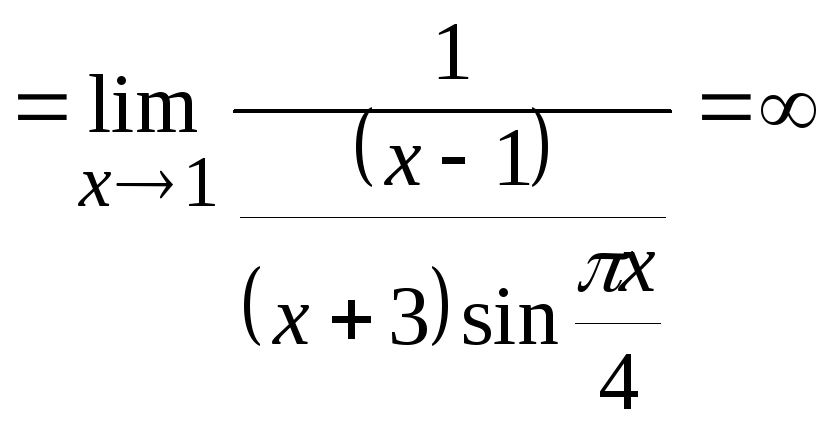 .
.
Ответ:
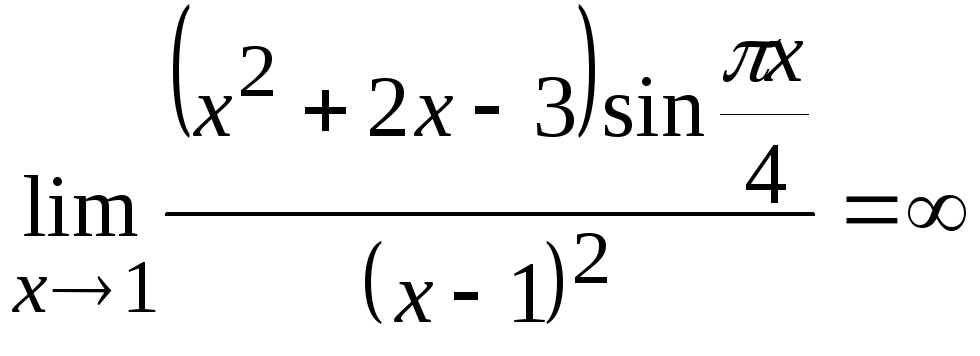 .
.
к)
Здесь возникает неопределенность типа
![]() .
Домножим числитель и знаменатель на
«сопряженное» к числителю иррациональное
выражение, затем разложим числитель и
знаменатель на множители и сократим их
на общий множитель, получим:
.
Домножим числитель и знаменатель на
«сопряженное» к числителю иррациональное
выражение, затем разложим числитель и
знаменатель на множители и сократим их
на общий множитель, получим:
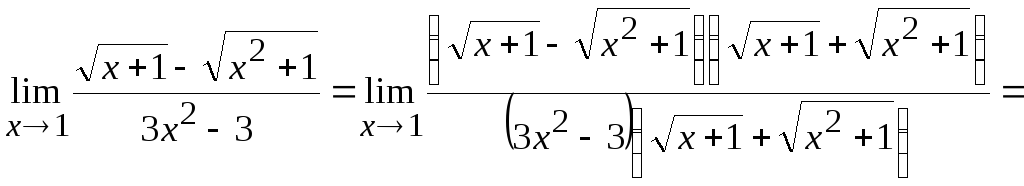
![]()
![]() .
.
Ответ:
![]() .
.
л)
Имеем неопределенность типа
![]() .
Домножим числитель и знаменатель на
одинаковые иррациональные выражения
так, чтобы в числителе появилась разность
квадратов, а в знаменателе – разность
кубов, затем разложим их на множители
и сократим их на общий множитель. Получим
.
Домножим числитель и знаменатель на
одинаковые иррациональные выражения
так, чтобы в числителе появилась разность
квадратов, а в знаменателе – разность
кубов, затем разложим их на множители
и сократим их на общий множитель. Получим
![]()
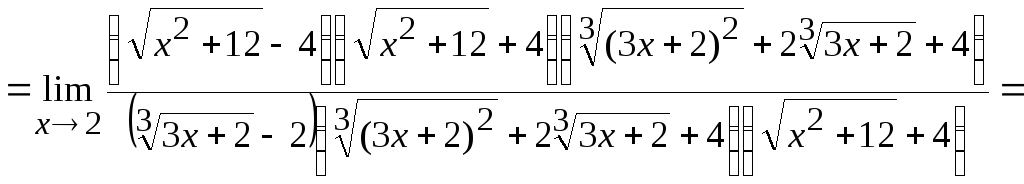
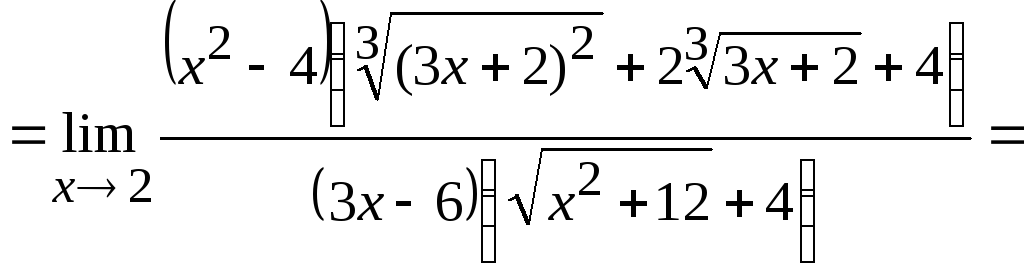

 .
.
Ответ:
![]() .
.
м)
Здесь следует рассмотреть два отдельных
случая:
![]() и
и
![]() .
Пусть
.
Пусть
![]() ,
используя теорему 4.2, получим
,
используя теорему 4.2, получим
![]() .
.
Пусть
![]() ,
тогда имеет место неопределенность
,
тогда имеет место неопределенность
![]() .
Умножим и разделим исходное выражение
на «сопряженное» выражение и воспользуемся
теоремой 4.1. Получим
.
Умножим и разделим исходное выражение
на «сопряженное» выражение и воспользуемся
теоремой 4.1. Получим
![]()
![]()
![]() .
.
Ответ:
искомый предел при
![]() не существует, существуют различные
пределы при
не существует, существуют различные
пределы при
![]() и при
и при
![]() :
:![]() ,
,
![]() .
.
н)
Здесь возникает неопределенность типа
![]() .
Приведем дроби к общему знаменателю,
затем разложим числитель и знаменатель
на множители и сократим их на общий
множитель. Получим
.
Приведем дроби к общему знаменателю,
затем разложим числитель и знаменатель
на множители и сократим их на общий
множитель. Получим
![]()
![]() .
.
Ответ:
![]() .
.
о)
При вычислении предела аргумента синуса
возникает неопределенность типа
![]() .
Вычислим этот предел:
.
Вычислим этот предел:
![]() .
.
Тогда по теореме 6.1 получим:
![]() .
.
Ответ:
![]() .
.
п)
Здесь при вычислении предела аргумента
логарифма возникает неопределенность
типа
![]() .
Вычислим этот предел:
.
Вычислим этот предел:
![]()
![]() .
.
По теореме 6.1 получим:
![]() .
.
Ответ:
![]() .
.
