2.4. Результат измерения. Доверительный интервал

Задачей эксперимента является нахождение истинного значения x₀ физической величины, которое может быть найдено, если имеется генеральная совокупность всех значений искомой величины Х. Однако, в связи с тем, что количество наблюдений в выборке конечно, в опыте находят некоторое приближенное к x₀ значение , называемое оценкой истинного значения, и указывают интервал, в который истинное значение x₀ попадает с заданной вероятностью P. Этот интервал называют доверительным интервалом, а вероятность Р – доверительной вероятностью.

В качестве оценки истинного значения согласно (2.2) выбирают среднее арифметическое результатов наблюдений в выборке

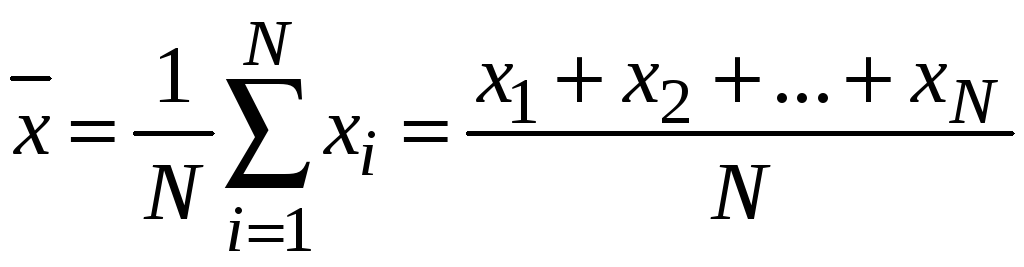, (2.7)

которое называют выборочным средним. Среднее также является случайной величиной, и если повторить опыт по его нахождению несколько раз, то получим выборку средних X: , , ..., , которые также будут отличаться друг от друга случайным образом, однако разброс средних значений будет заметно меньше разброса результатов отдельных наблюдений в каждой выборке.

Для нахождения доверительного интервала необходимо знать распределение средних значений около x₀. Зная вид , можно построить интервал, в который истинное значение x₀ попадает с вероятностью Р. Для этого на оси абсцисс (рис. 2.2) находят точки x₁ и x₂ такие, чтобы площади под графиком слева от x₁ и справа от x₂ равнялись бы одной и той же величине . Тогда площадь под графиком в интервале (x₁, x₂) будет равна значению вероятности P, и для произвольного полученного в опыте среднего значения можно написать: x₁ << x₂ c вероятностью Р:

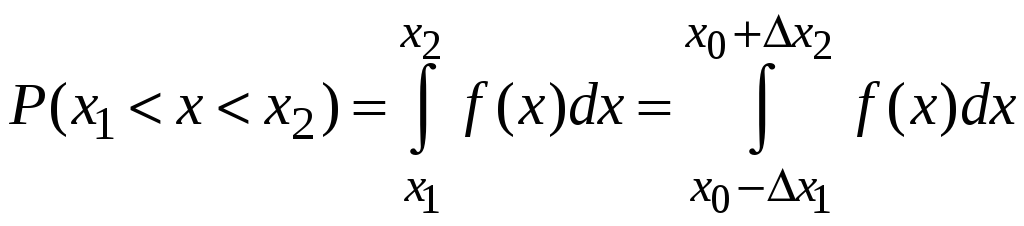. (2.8)

Границы интервала можно также записать в виде , . Если распределение симметрично, то . Величину в этом случае называют случайной доверительной погрешностью результата измерения.

2.5. Нормальное или гауссовское распределение

Одним из часто встречающихся на практике распределений является нормальный или гауссовский закон. Ему подчиняются физические величины, случайность которых обусловлена действием множества независимых (или слабо зависимых) малых аддитивных факторов, результат воздействия каждого из которых мал по сравнению с их суммарным воздействием. Плотность распределения вероятности нормального закона имеет вид

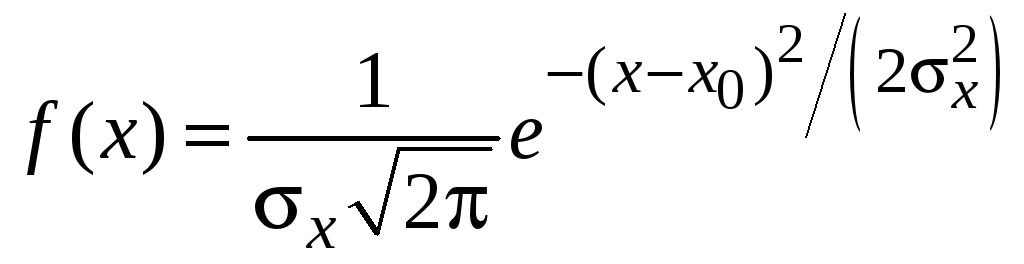, (2.9)

где x – случайное значение величины X. Параметр x₀ определяет центр распределения, а _x – форму и ширину кривой плотности рас­пределения (рис. 2.3). Множитель 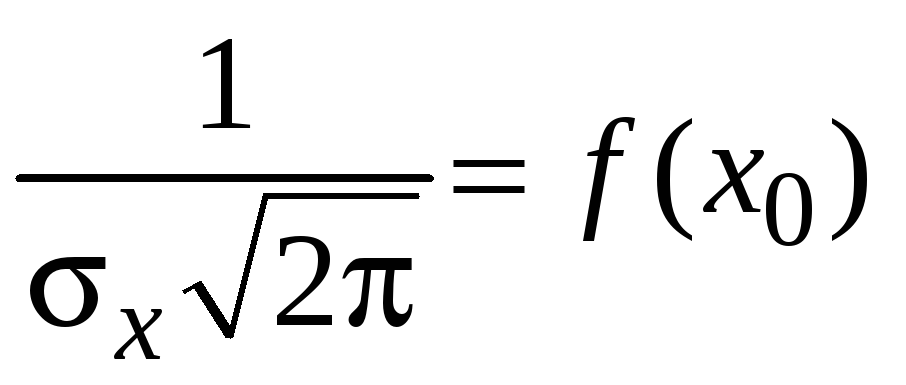перед экспонентой, определяющий высоту гауссовской кривой, выбран таким образом, чтобы было выполнено условие нормировки (2.4).

П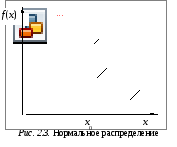 оскольку Гауссово распределение симметрично относительно x₀, согласно (2.8) вероятность того, что случайное значение x величины X, распределенной по нормальному закону, попадет в заданный интервал (x₁, x₂), будет определяться выражением

. (2.10)

Вводя обозначение , называемую стандартизованной переменной, (2.10) можно записать в виде

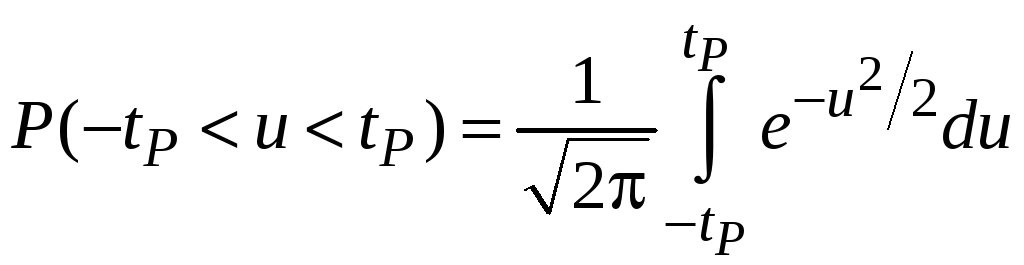, (2.11)

где t_P – коэффициенты, определяющие ширину интервала в единицах параметра нормального распределения _x: . Вероятности P попадания u в интервал (–t_P, t_P) можно найти, вычислив интеграл (2.11) численно для различных значений ширины интервала t_P. И обратно, каждой заранее заданной вероятности P будет соответствовать свое конкретное значение коэффициента t_P, зависящее от выбора доверительной вероятности P. Если значения коэффициентов t_P найдены, то от переменной u можно вернуться к переменной x. Тогда из неравенства получим с вероятностью P.

Можно показать (см. 2.6), что если значения x величины X распределены по нормальному закону, то и рассчитываемые по ним средние значения также распределены по нормальному закону с центром в точке x₀ и шириной распределения , где N – объем выборок, по которым рассчитываются . Распределение средних будет описываться формулой (2.9), в которой x заменено на , а на .

Если средние значения распределены по нормальному закону, то задача нахождения доверительного интервала сводится к нахождению доверительного интервала (–t_P, t_P) для стандартизованной переменной и переходу к доверительному интервалу переменной . В результате получим, что границы интервала, в который случайное значение попадает с вероятностью P, определяются неравенством . Откуда для границ доверительного интервала x₀ получаем , где t_P – коэффициенты, соответствующие заданной вероятности Р. Это неравенство принято записывать в виде символического равенства

с вероятностью P, (2.12)

где – случайная доверительная погрешность результата измерения.