Міністерство освіти України

Український державний університет водного господарства

та природокористування

085-121

Лінійна алгебра та аналітична геометрія

Конспект лекцій для студентів

спеціальностей 6.050.100, 6.100.400

денної форми навчання.

Затверджено на засіданні

методичної комісії

факультету менеджменту

протокол №

від 2003р.

Рівне – 2003

Конспект лекцій “Лінійна алгебра та аналітична геометрія”

Давидюк Г.П. – Рівне: Український державний університет водного господарства та природокористування 2002, с.

Упорядник: Давидюк Г.П. – к.ф. – м.н., ст. викладач.

Відповідальний за випуск завідувач кафедри вищої

математики Ярмуш Я.І., к.ф. – м.н., доцент

I Елементи лінійної алгебри

В цьому розділі розглянемо визначники, матриці та їх застосування до розв’язування систем лінійних рівнянь.

Визначники, їх обчислення та властивості

Прямокутна таблиця упорядкованих чисел (або інших інших об’єктів), взяті в круглі дужки, в математиці називається матрицею.

Число рядочків і стовпчиків становлять розміри матриці.

Матриці позначаються великими буквами латинського алфавіту, а їх елементи відповідними маленькими буквами з двома індексами. Перший індекс – номер рядочка, другий – номер стовпчика даного елемента.

Наприклад: матриця:

А=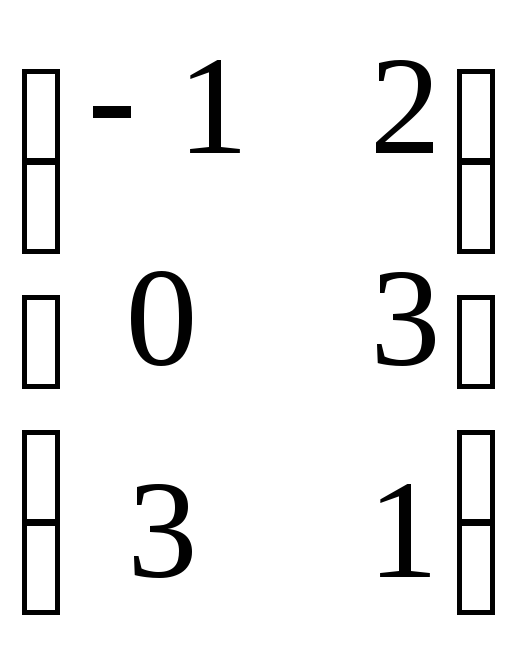 (3х2) а₂₂=3

Матриця, в якій число рядочків і стовпчиків однакове називається - квадратною.

У відповідність квадратній матриці можна поставити число за певним законом яке, називається визначником або детермінантом і позначається det A, , або вертикальними рисками, що обмежують елементи матриці.

Визначником 2-го порядку – називається число, яке ставиться в відповідність матриці розміром (2х2) за таким законом:

= ₁₁₂₂ - ₁₂₂₁

Визначником 3-го порядку – називається число, яке ставиться у відповідність матриці розмірами (3х3) за таким законом:

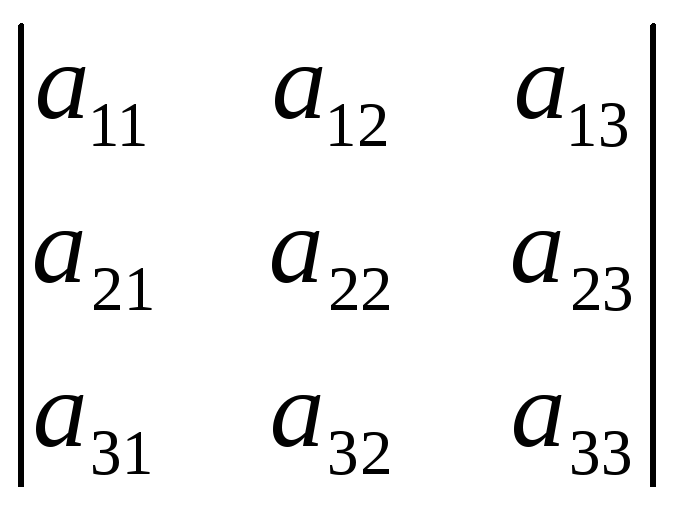= ₁₁₂₂₃₃+₁₃₂₁₃₂+₃₁₁₂₂₃+₁₃₂₂₃₁-₁₁₂₃₃₂-₃₃₁₂₂₁

Для обчислення визначника 3-го порядку можна користуватися правилом, трикутника або правилом Саррюса.

Схеми обчислення:

а) Правило трикутника: б) Правило Саррюса

” +“ ”- “ ” +“ ”- “

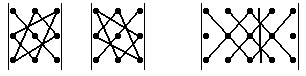
Для обчислення визначника n-го порядку розглянемо поняття мінора та алгебраїчного доповнення до даного елемента.

Означення: Мінором ij до елемента _ij матриці А називається визначник на одиницю меншого порядку, утворений із даного викреслюванням і-го рядочка і j-го стовпчика на перетині яких стоїть цей елемент.

Наприклад:

А= ₁₃=0 М₁₃==3

Означення: Алгебраїчним доповненням А_ij до елемента _ij називається мінор взятий зі знаком “+” якщо сума індексів i+j число парне, або взятий зі знаком “-“ , якщо сума i+j не парне число.

A_ij = (-1)^i+jM_ij Наприклад: A₁₃ = (-1)¹⁺³ 3=3

Визначником n-го порядку називається число, яке ставиться у відповідність матриці розміру (nxn) і дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх відповідні алгебраїчні доповнення.

Наприклад: визначник розкладений на елементи 1-го рядка:

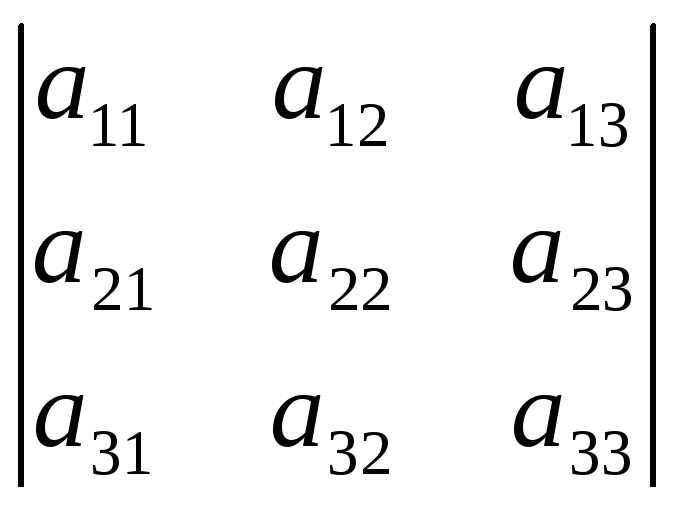= ₁₁А₁₁+₁₂А₁₂₁₃А₁₃

ЗАУВАЖЕННЯ: Розкладати визначник за елементами рядка або стовпця доцільно в тому випадку, коли є рядочки або стовпчики які містять велику кількість нулів. Якщо ж їх немає, то при бажанні за допомогою властивості визначників можна їх зробити.

Наприклад: обчислити визначник 4-го порядку.

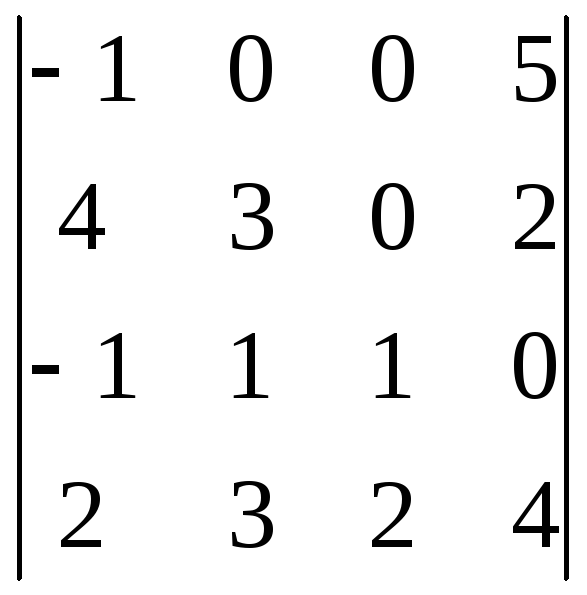= 0А₁₃+0А₂₃+1А₃₃+2А₄₃=124+2(-37)=24-74=-50, де

А₃₃== -12+0+60-36-0+6=24 А₄₃= -= -(0+0+20+15-0+2)= -37

Властивості визначників:

1. Якщо у визначнику поміняти місцями всі рядки на відповідні стовпці або навпаки, то визначник не зміниться.

2. Якщо у визначнику поміняти місцями будь-які два рядки (стовпці), то визначник змінює знак на протилежний.

3. Якщо елементи будь-якого рядка або стовпця мають спільний множник, то його можна винести за знак визначника:

=

4. Визначник дорівнює нулю, якщо в ньому є рядочок або стовпчик з всіма нульовими елементами.

Наприклад:

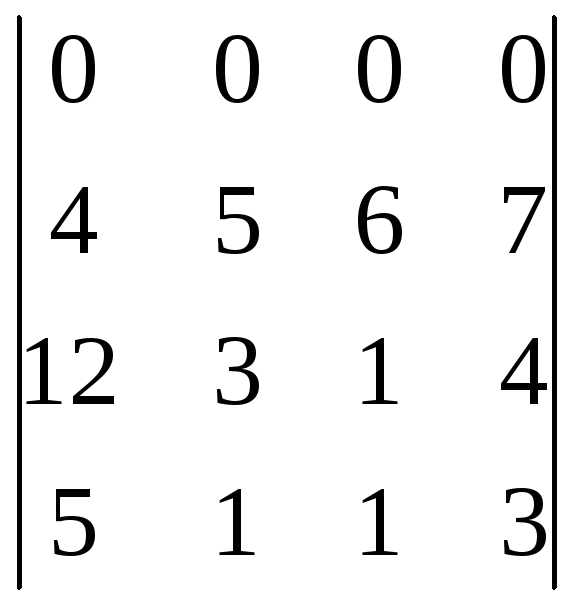
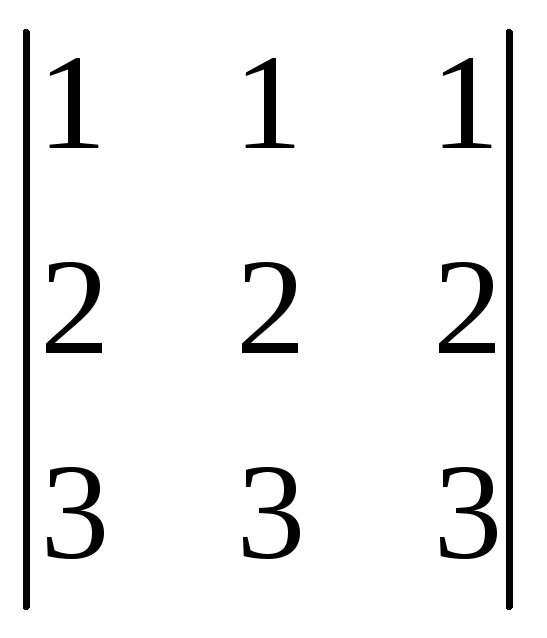
5. Визначник дорівнює нулю, якщо в ньому є два однакові рядки або стовпці.

6. Визначник дорівнює нулю, якщо в ньому є пропорційні рядки або стовпці.

7. Якщо у визначнику елементи деякого стовпця (рядка) являють собою суму двох доданків то такий визначник можна представити у вигляді сумі двох визначників:

= +

8. Якщо до елементів деякого рядка (стовпця) додати відповідні елементи іншого рядка (стовпця) помножені на деяке число, то визначник не зміниться.

9. Якщо елементи деякого рядка (стовпця) помножити на алгебраїчні доповнення до іншого рядка (стовпця) то отримана сума дорівнює нулю.

Щоб переконатися у будь-якій з властивостей, достатньо обчислити визначники у рівностях.

Системи лінійних рівнянь з трьома невідомими. Правило Крамера.

Нехай задана система трьох рівнянь з трьома невідомими:

(1)

де , - числа, коефіцієнти при невідомих,; ,

b,b,b- числа, вільні члени ;x,y,z – невідомі.

Розглянемо для системи (1) головний визначник, складений із коефіцієнтів при невідомих та допоміжні визначники:

, =

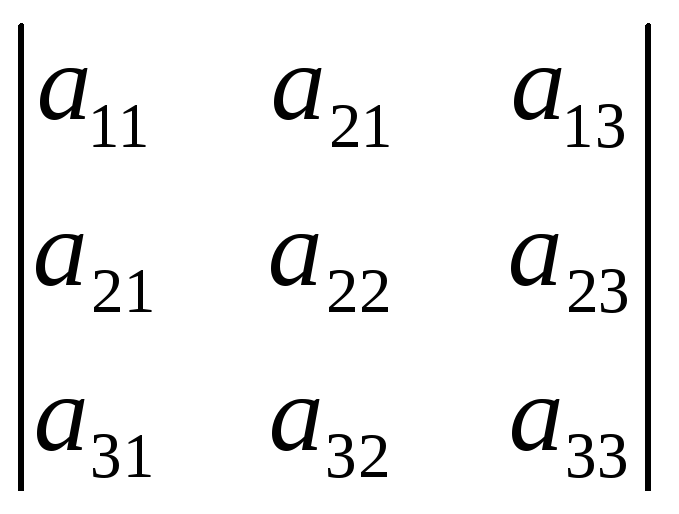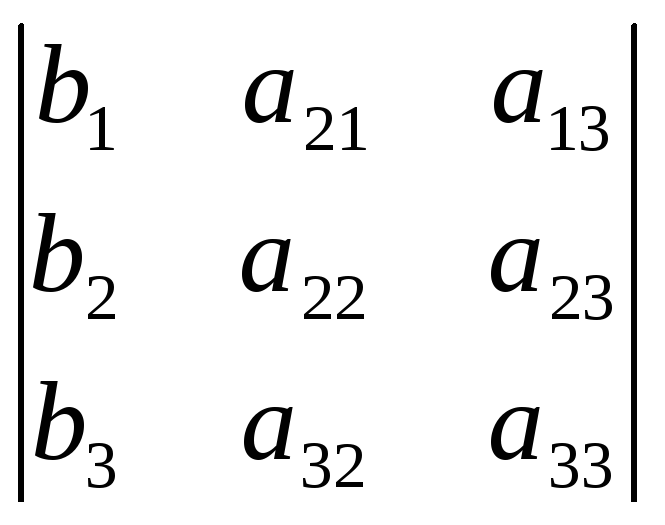
y=,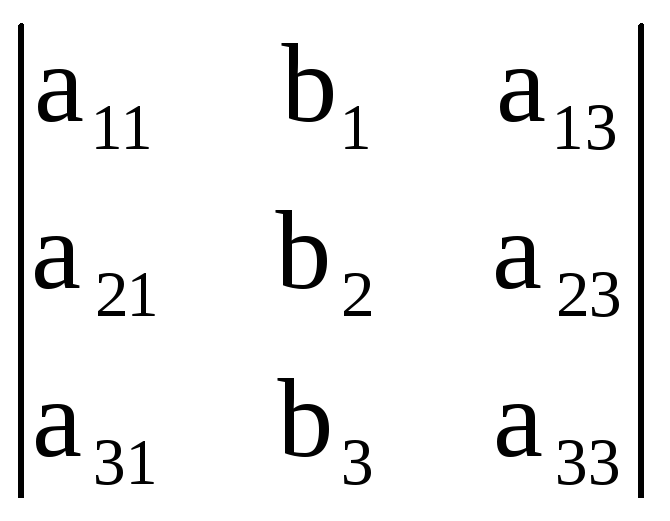

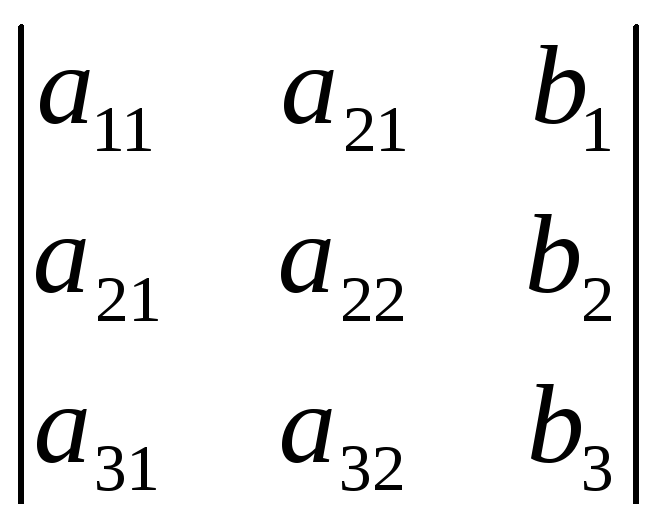
Помножимо перше рівняння системи (1) на значення А, друге рівняння – на А, третє – на А і знайдемо суму трьох рівнянь. Зібравши коефіцієнти більше x, y, z одержимо:

x(A + A + A) + y(A + A + A) + z(A + A + A)= bA+bA+bA

=

Аналогічно, якщо рівняння системи (1) помножити на А, друге - на А, третє - на А і знайти їх суму, звести подібні члени біля невідомих x, y, z, то отримаємо рівняння:

Y=y

Якщо перше рівняння системи (1) помножити на А, друге - на А, третє на - А і зробивши аналогічну процедуру як в попередньому рівнянні то отримаємо рівняння, Z=z

Тоді систему (1) можна записати у вигляді (2)

(2)

Дослідимо систему (2):

1. Якщо головний визначник системи , то система має єдиний розв’язок

X= Y= Z= (3)

Формули називаються формулами Крамера

2. Якщо головний визначник =0, а хоч би один з допоміжних х, у, z відмінний від нуля, то система не має розв’язків, тобто несумісна .

3. Якщо=0, x=y=z=0, то система має безліч розв’язків, або сумісна.

Якщо перше або друге рівняння є наслідком попередніх, то система має безліч розв’язків.

Приклад 1:

==0

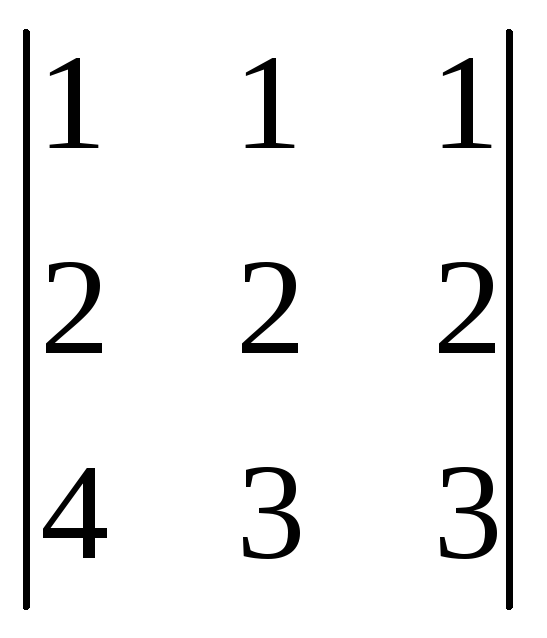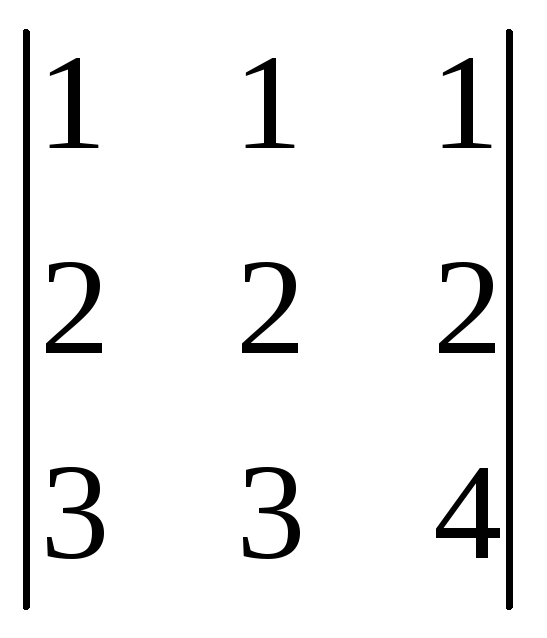x==0 у==0 z==0

Система не сумісна, третє рівняння не може бути наслідком першого

Приклад 2:

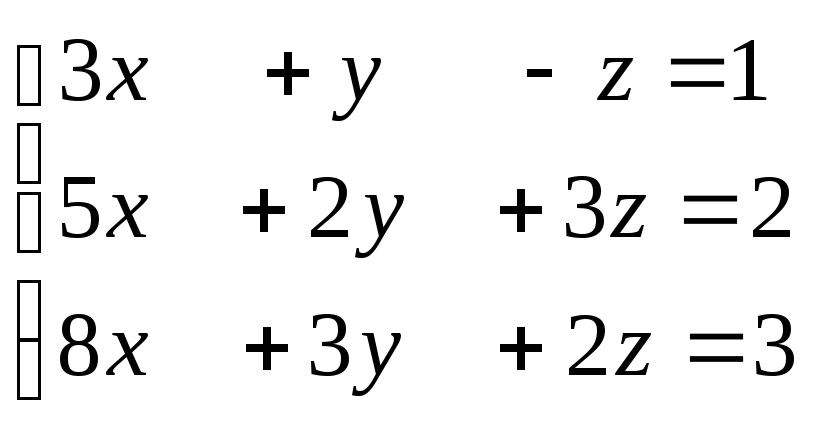
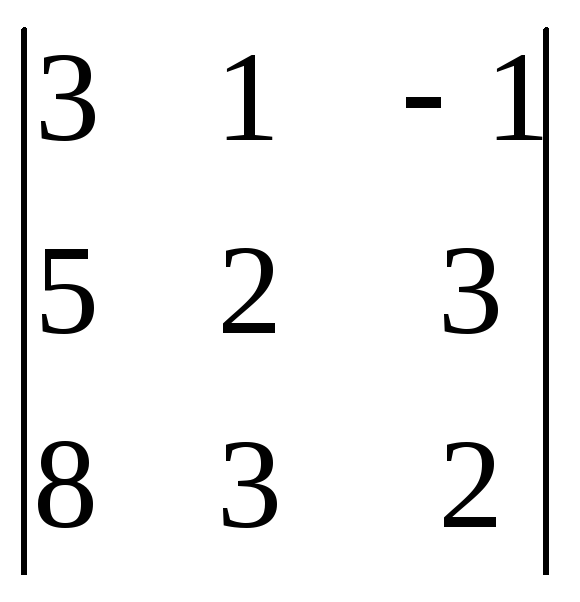== 12+24-15+16-27-10=28-28=0х==0 у==0

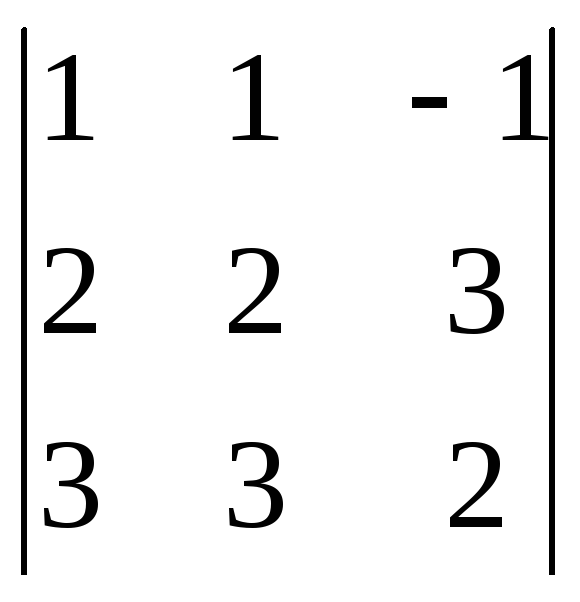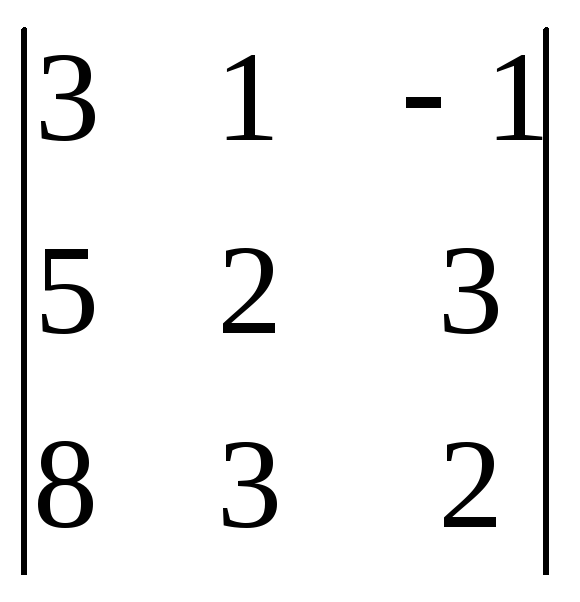z==0

Третє рівняння є наслідком першого і другого (їх сума), тому його відкидаємо. Отримаємо систем двох рівнянь з трьома невідомими.

Одну із змінних будемо вважають вільною, її переносимо до вільного члена. Нехай z є R.

==6-5=10 х==(1+z)2-1(2-3z)=2+2z-2+3z=5z

y==3(2-3z)-5(1+z)=6-9z-5-5z=1-14z Отже X== Y===1-14z

Система має безліч розв’язків х=5z, y=1-14z, zєR (z вільна змінна)

При z=0 отримаємо розв’язок системи

x=5 0=0 y=1-14 0=0 z=0

Зауваження: Іноді для зручності z прирівнюють до числового параметра t, (z=t), тоді дану сукупність розв’язків записують так:

x=5t y=1-14t z=t

Деякі види матриць. Дії над ними. Обернена матриця.

Матрицю, всі елементи якої дорівнюють нулю, називають нульовою, і позначають 0

Квадратна матриця називається діагональною якщо всі її елементи, за винятком елементів головної діагоналі, дорівнюють нулеві. Діагональна матриця з одиничними по головній діагоналі, називається одиничною і позначається Е.

Квадратні матриці, визначник яких дорівнює нулеві називаються виродженими. Квадратні матриці, визначник яких відмінний від нуля, називають невиродженими або неособливими.

Дві матриці однакового розміру називаються рівними, якщо рівні їх відповідні елементи.

Сумою (різницею) двох матриць однакового розміру є матриця відповідні елементи якої дорівнюють сумі (різниці) даних елементів.

А=В= А+В= A-B=

Добутком матриці на число є матриця, всі елементи якої збільшені в раз.

Дві матриці можна множити лише такі, у яких число стовпчиків першої матриці дорівнює числу рядочків другої матриці.

Добутком матриці А розміром (nxk) на матрицю В розміром (кxm) називається матриця С розміру (nxm), елементи якої знаходяться за формулою:

C_ij=b_ej

Наприклад: А=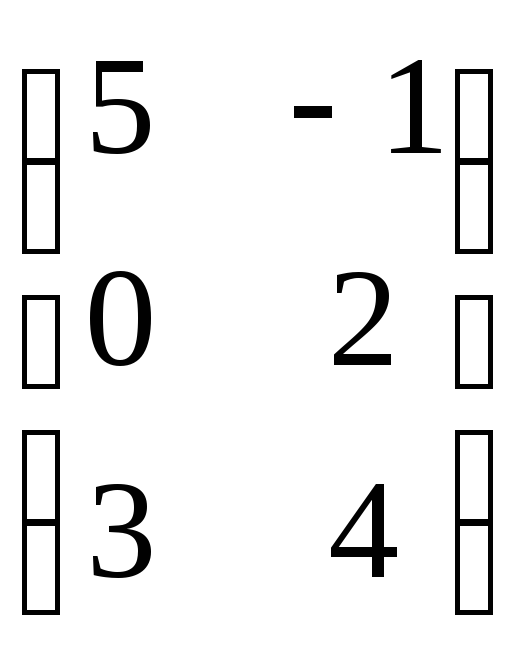 матриця розміру (3х2) В=матриця розміром (3х2)

Добуток таких матриць знайти неможливо.

Якщо. А=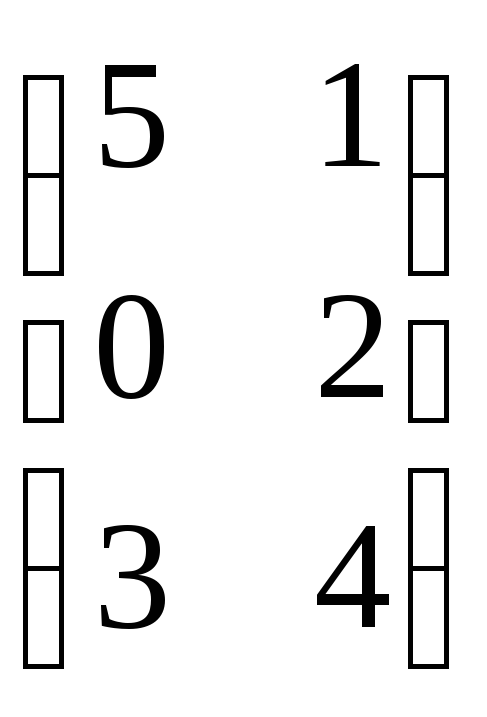 матриця розміру (3х2) В= матриця розміру (2х2), то

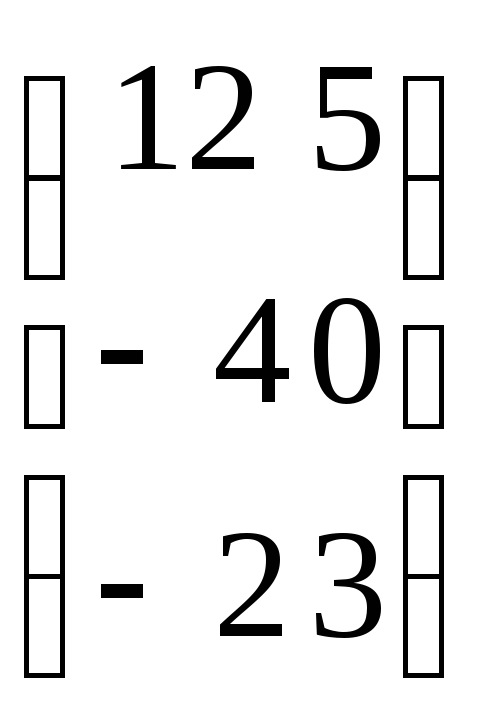
АВ===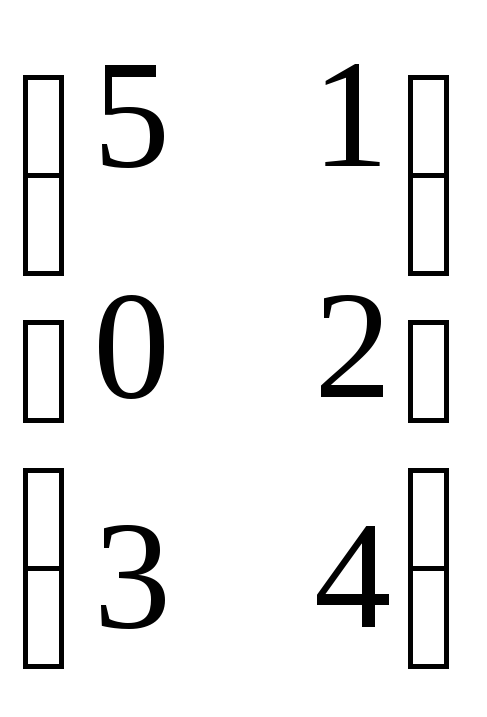

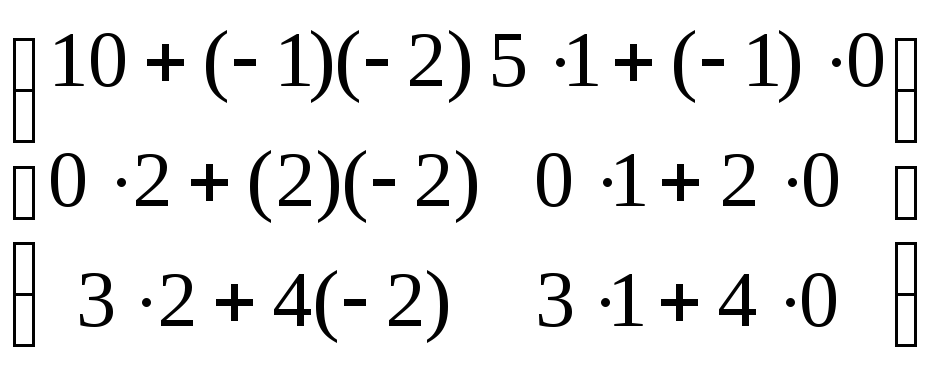Добуток двох ненульових матриць може бути нульова матриця

Наприклад х==

Для довільних матриць А, В, С, та будь-яких чисел та справедливі співвідношення:

1. А+В=В+А; 7. (А)=()А

2. А+(В+С)=(А+В)+С;

3. А+0=А;

4. А+(-А)=0;

5. (А+В)= А+В;

6. (+)А=А+А

Матриця Аназивається оберненою до матриці А, якщо АА=Е.(одинична матриця) або А А=Е.

Поняття оберненої матриці нам треба для розв’язування системи рівнянь.

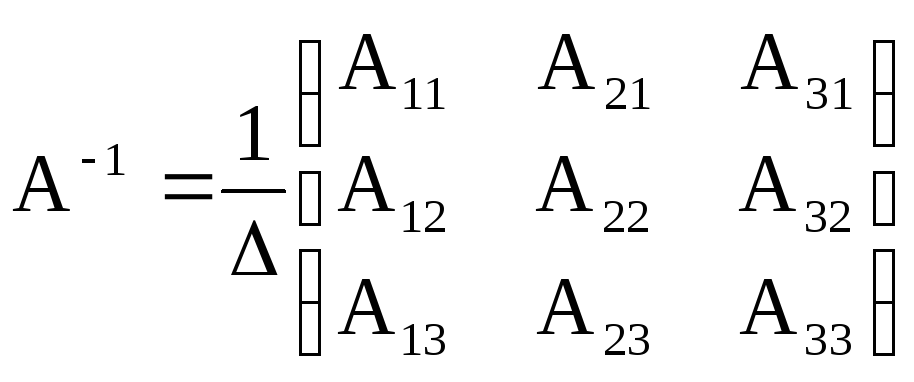
Знайдемо обернену матрицю до матриці третього порядку.

A=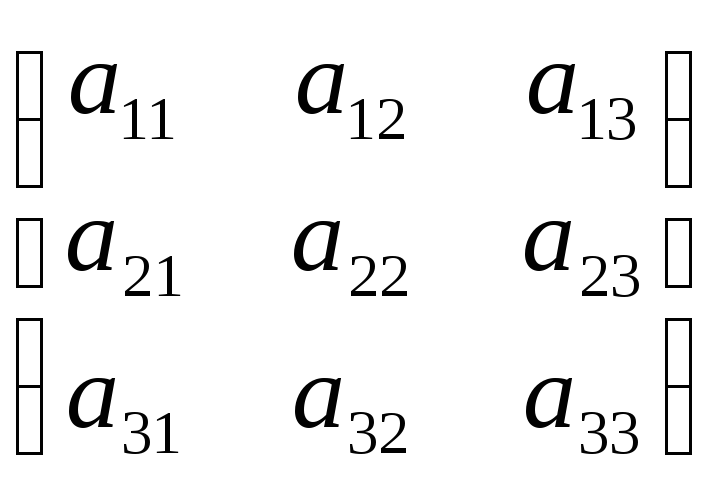-обернена матриця існує для не вироджених матриць. detA0

А=

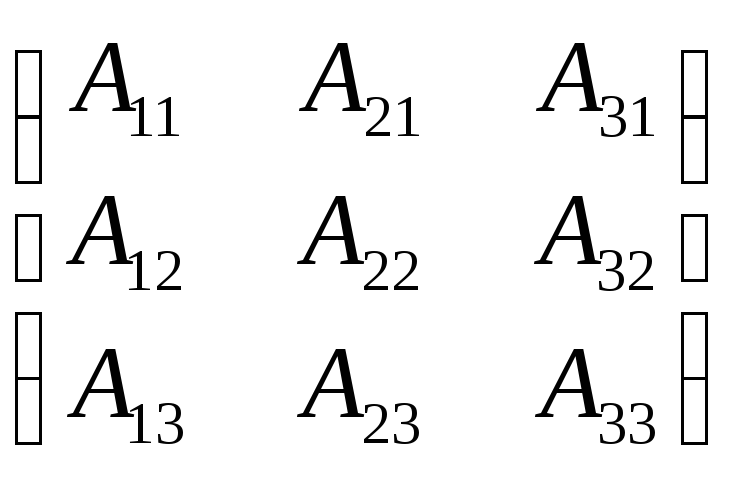
Зауваження: При знаходженні оберненої матриці алгебраїчні доповнення до рядків треба ставити у відповідні стовпчики.

Приклад:

АA==

=

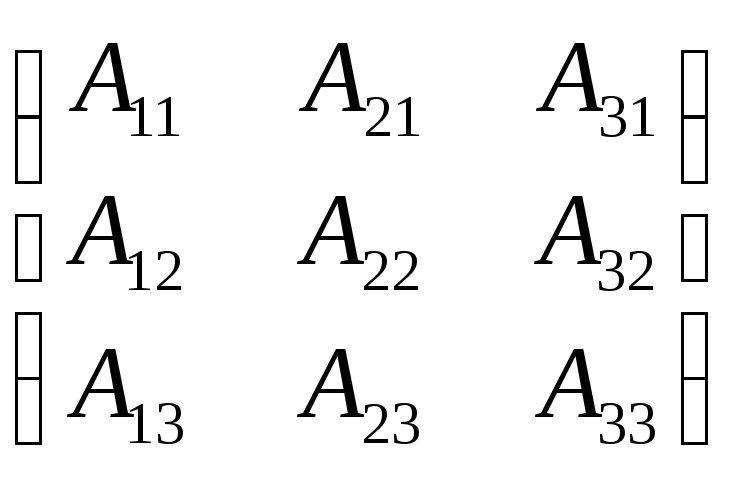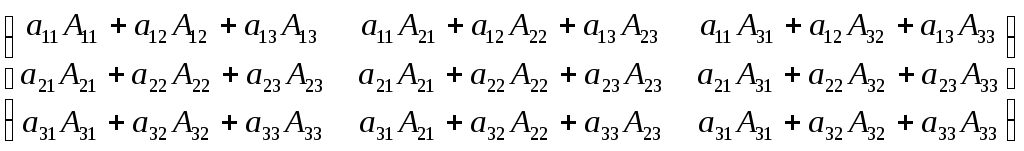==E

Розв’язування лінійних систем матричним способом.

Нехай задана система трьох рівнянь з трьома невідомими:

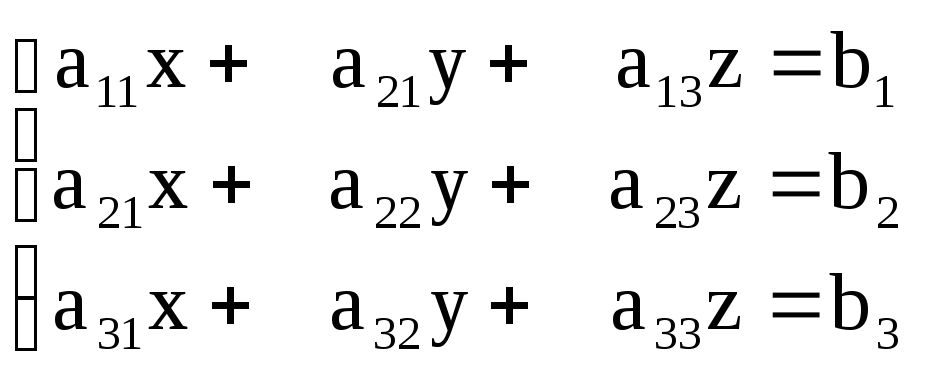(1)

Якщо позначити A=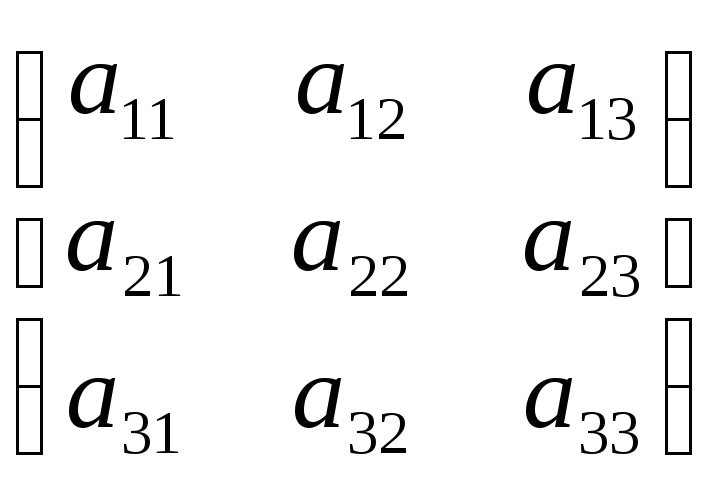, В=, Х= , то систему (1) можна записати у матричному вигляді (2): АХ=В (2)

Якщо матриця невироджена, то із рівняння (2) можна знайти Х: Х=АВ (3)

Наприклад розв’язати систему рівнянь матричним способом

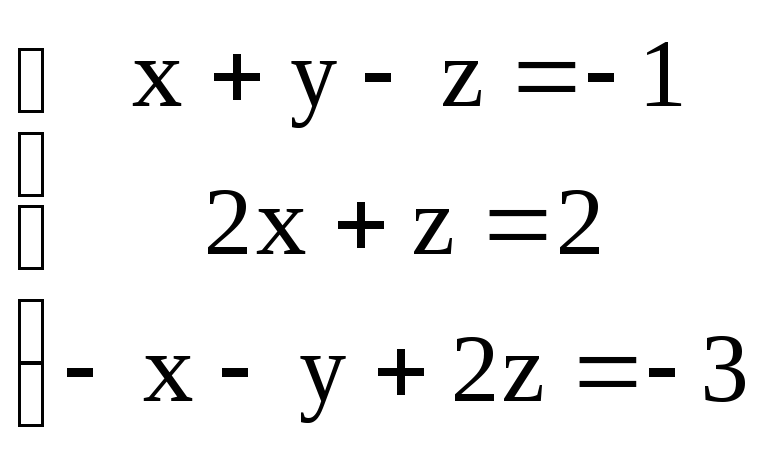
Запишемо дану систему рівнянь у матричному вигляді АХ=В, де

А=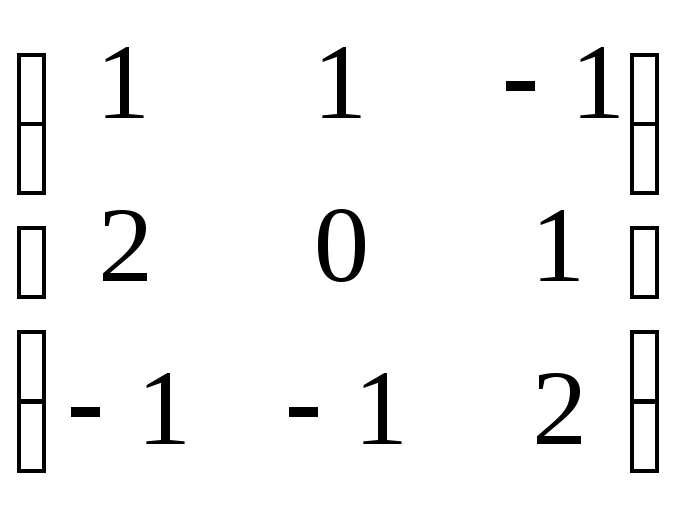, В=, Х=

Знайдемо головний визначник матриці А

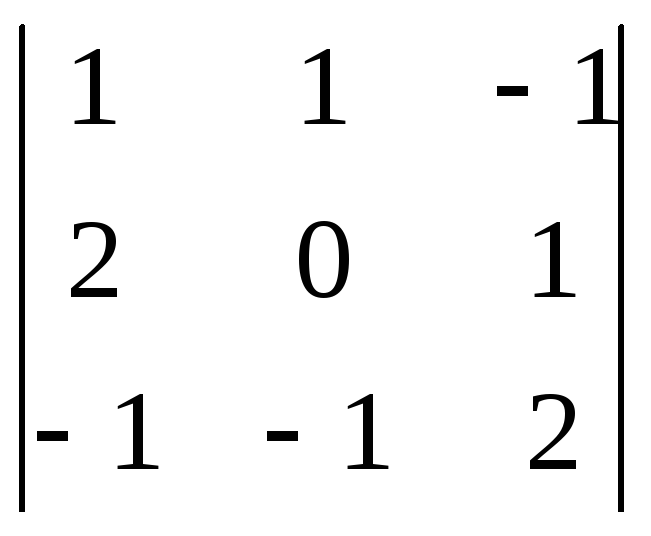==1А+1А-1А=1+1(-5)-1(-2)=1-5+2=-20,

А=-=-(4+1)=-5 А==0+1=1 А==-2-0=-2

Оскільки матриця А вироджена, то Х=АВ, де

Так як

=-1

=1

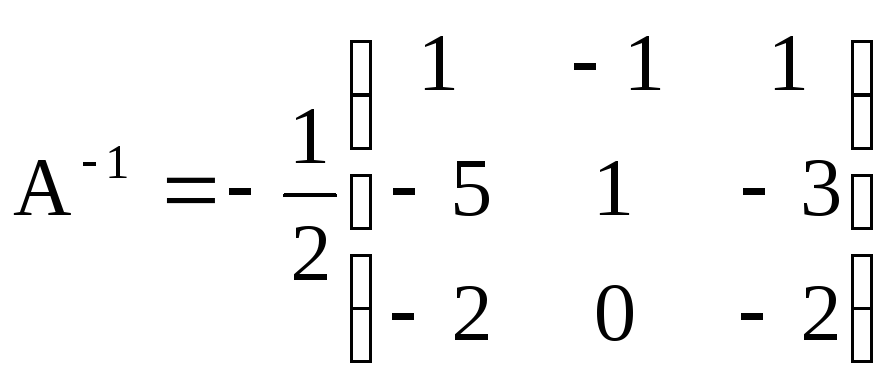
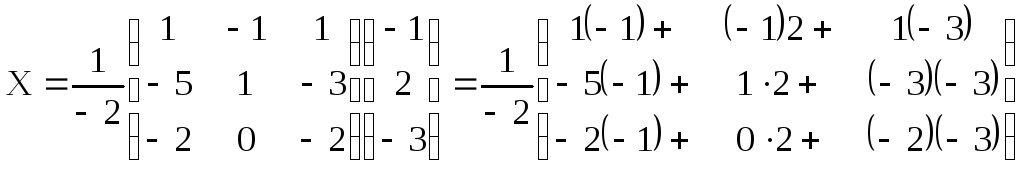
Отже, х = 3, у = -8, z = -4 – розв'язок заданої системи