
- •К русскому читателю
- •Как пользоваться книгой
- •Что такое математика?
- •Натуральные числа
- •Введение
- •Операции над целыми числами
- •Бесконечность системы натуральных чисел. Математическая индукция
- •Введение
- •Математическая числовая система
- •Введение
- •Рациональные числа
- •Несоизмеримые отрезки. Иррациональные числа, пределы
- •Рациональные числа и периодические десятичные дроби.
- •Замечания из области аналитической геометрии
- •Математический анализ бесконечного
- •Комплексные числа
- •Алгебраические и трансцендентные числа
- •Геометрические построения. Алгебра числовых полей
- •Введение
- •Основные геометрические построения
- •Неразрешимость трех классических проблем
- •Геометрические преобразования. Инверсия
- •Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля
- •Еще об инверсии и ее применениях
- •Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- •Введение
- •Основные понятия
- •Двойное отношение
- •Параллельность и бесконечность
- •Применения
- •Аналитическое представление
- •Конические сечения и квадрики
- •Аксиоматика и нееклидова геометрия
- •Топология
- •Введение
- •Формула Эйлера для многогранников
- •Топологические свойства фигур
- •Другие примеры топологических теорем
- •Топологическая классификация поверхностей
- •Приложение
- •Функции и пределы
- •Введение
- •Независимое переменное и функция
- •Пределы
- •Пределы при непрерывном приближении
- •Точное определение непрерывности
- •Две основные теоремы о непрерывных функциях
- •Теорема Вейерштрасса об экстремальных значениях.
- •Некоторые применения теоремы Больцано
- •Максимумы и минимумы
- •Введение
- •Задачи из области элементарной геометрии
- •Общий принцип, которому подчинены экстремальные задачи
- •Стационарные точки и дифференциальное исчисление
- •Треугольник Шварца
- •Проблема Штейнера
- •Экстремумы и неравенства
- •Существование экстремума. Принцип Дирихле
- •Экстремальные проблемы элементарного содержания.
- •Изопериметрическая проблема
- •Вариационное исчисление
- •Вариационное исчисление. Принцип Ферма в оптике.
- •Экспериментальные решения задач на минимум. Опыты с мыльными пленками
- •Математический анализ
- •Введение
- •Интеграл
- •Примеры интегрирования. Интегрирование функции xr.
- •Производная
- •Техника дифференцирования
- •Обозначения Лейбница и «бесконечно малые»
- •Основная теорема анализа
- •Определение и свойства логарифма. Эйлерово число e.
- •Дифференциальные уравнения
- •Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- •Дополнительные замечания. Задачи и упражнения
- •Арифметика и алгебра
- •Аналитическая геометрия
- •Геометрические построения
- •Проективная и неевклидова геометрия
- •Топология
- •Функции, пределы, непрерывность
- •Максимумы и минимумы
- •Дифференциальное и интегральное исчисления
- •Техника интегрирования
- •О создании книги «Что такое математика?»
- •Рекомендуемая литература
- •Предметный указатель
388 |
МАКСИМУМЫ И МИНИМУМЫ |
гл. VII |
меньшей.1 Решение этой задачи имеет тот или иной вид в зависимости от рас-
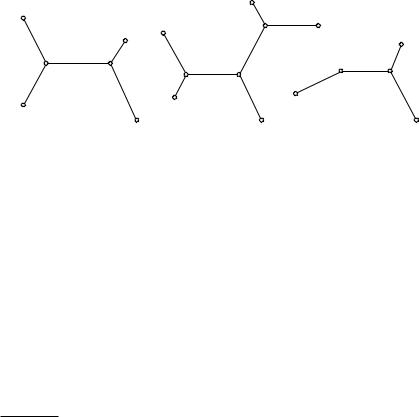
положения данных точек. Читатель с пользой сможет заняться более внимательным рассмотрением этого вопроса, исходя из проблемы Штейнера. Мы ограничимся здесь указанием результатов в типических примерах, изображенных на рис. 216–218. В первом примере решение дается системой из пяти отрезков с двумя «кратными точками», в которых сходятся по три сегмента, образуя между собой углы в 120◦. Во втором примере число кратных точек равно трем. При некоторых иных расположениях данных точек указанные фигуры не получаются: возможны случаи «вырождения», когда какая-нибудь одна из данных точек (или несколько таких точек) становится сама «кратной точкой» сети — таков третий из приведенных примеров.
A5
A1 |
|
A4 |
|
|
A1 |
||
A4 |
A4 |
||
|
|||
|
|
||
|
|
A2 |
|
A2 |
A2 |
A1 |
|
|
|
||
A3 |
A3 |
A3 |
Рис. 216–218. Кратчайшая система путей, соединяющих данные точки
Если число данных точек равно n, то всего будет не более n − 2 кратных точек, в которых сходятся по три отрезка, образуя углы в 120◦.
Решение проблемы не всегда единственно. Так, если четыре данные точки расположены в вершинах квадрата, то возникают два эквивалентных решения (рис. 219, 220). Если точки A1, A2, . . . , An являются вершинами ломаной линии с углами при вершинах, достаточно близкими к 180◦, то сама ломаная является решением.
§ 6. Экстремумы и неравенства
Одной из характерных черт высших разделов математики является та выдающаяся роль, которую в них играют неравенства. В сущности, любая максимальная проблема всегда приводит к неравенству, выражающему тот факт, что рассматриваемая переменная величина не превышает некоторого максимального значения, доставляемого решением этой
1Выработка общих методов для решения прикладных задач типа описанной составила в последние годы предмет так называемого линейного программирования; см., например, [60]. — Прим. ред.

§ 6 |
ЭКСТРЕМУМЫ И НЕРАВЕНСТВА |
389 |
проблемы. Во многих случаях получаемые таким образом неравенства заслуживают внимания и независимо от экстремальной проблемы, к ним приводящей. В качестве примера мы рассмотрим сейчас важное неравенство, связывающее арифметическое и геометрическое средние.
1. Среднее арифметическое и среднее геометрическое двух положительных величин. Займемся прежде всего очень простой максимальной проблемой, с которой часто приходится встречаться и в самой математике, и в ее приложениях. В геометрической формулировке проблема эта заключается в следующем: среди всех прямоугольников с наперед заданным периметром найти тот, который имеет наибольшую площадь. Решением, как нетрудно догадаться, является квадрат. Доказать это можно следующим рассуждением. Пусть заданный периметр равен 2a. Тогда сумма x + y длин двух прилежащих сторон прямоугольника x и y равна постоянной величине a, а в максимум следует обратить произведение xy. «Среднее арифметическое» величин x и y есть не что иное, как выражение
|
|
m = |
x + y |
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||
Введем еще величину |
|
|
|
|
|
|
|
|
|||||||
|
|
d = |
x − y |
, |
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|||||
причем получатся соотношения |
|
|
|
|
|
|
|
|
|||||||
|
|
x = m + d, |
y = m − d; |
|
|
||||||||||
из них вытекает, что |
|
|
|
|
|
|
|
|
|||||||
|
|
xy = (m + d)(m − d) = m2 |
− d2 = |
x |
+ y |
|
2 |
||||||||
|
|
|
− d2. |
||||||||||||
Так как d |
2 |
|
2 |
||||||||||||
|
не может быть отрицательно, а обращается в нуль только |
||||||||||||||
при x = y, то мы немедленно приходим к неравенству |
|||||||||||||||
|
|
√ |
|
6 |
x + y |
, |
|
|
(1) |
||||||
|
|
xy |
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
причем знак равенства здесь возможен только при d = 0, т. е. при x = y.
Рис. 219–220. Кратчайшие системы путей, соединяющие вершины квадрата
390 |
МАКСИМУМЫ И МИНИМУМЫ |
|
|
гл. VII |
|||
Так как x + y имеет постоянное значение a, то отсюда следует, что |
|||||||
выражение |
√xy, а значит, и интересующая нас площадь xy принимают |
||||||
наибольшие возможное значение при x = y. Выражение |
|
|
|||||
|
|
g = |
√xy, |
|
|
|
|
где радикал взят в арифметическом смысле — со знаком +,— называет- |
|||||||
ся «средним геометрическим» положительных величин x и y; неравен- |
|||||||
ство (1) выражает основное соотношение между средними арифметиче- |
|||||||
ским и геометрическим. |
|
|
|
|
|
||
Неравенство (1) вытекает также непосредственно из того факта, что |
|||||||
выражение |
(√x − |
√y)2 = x + y − 2√xy, |
|
|
|
||
|
|
|
|
||||
будучи точным квадратом, не может быть отрицательным и обращается |
|||||||
в нуль только при x = y. |
|
|
|
|
|
||
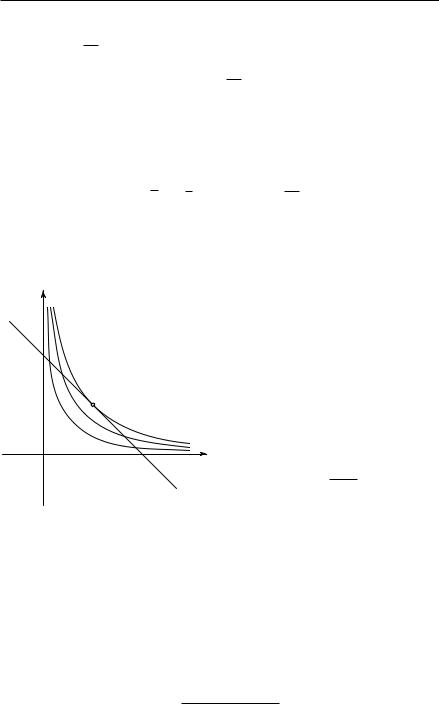
Вот еще геометрический вывод того же неравенства. Рассмотрим в |
|||||||
плоскости x, y неподвижную прямую линию x + y = 2m и вместе с ней |
|||||||
|
|
|
семейство кривых (гипербол) xy = |
||||
y |
|
|
c, причем c постоянно для каждой |
||||
|
|
|
кривой, но меняется при перехо- |
||||
|
|
|
де от одной кривой к другой. Из |
||||
|
|
|
рис. 221 ясно, что кривой, имею- |
||||
|
|
|
щей хоть одну общую точку с на- |
||||
|
|
|
шей прямой линией и соответству- |
||||
|
|
|
ющей наибольшему значению c, |
||||
|
|
|
является та гипербола, которая ка- |
||||
|
|
|
сается прямой в точке x = y = m; |
||||
|
|
|
для этой гиперболы, следователь- |
||||
O |
|
x |
но, c = m2. Итак, |
|
|
||
|
|
+ y |
2 |
||||
|
|
|
|
||||
|
x |
|
xy 6 |
x 2 |
. |
||
|
|
|
Следует заметить, |
что всякое |
|||
Рис. 221. Минимум xy при заданном |
неравенство вида f(x, y) 6 g(x, y) |
||||||
можно прочесть двумя способами, |
|||||||
значении x + y |
|
||||||
и потому оно порождает как максимальное, так и минимальное свойства. |
|||||||
Например, неравенство (1) выражает также тот факт, что среди всех |
|||||||
прямоугольников с данной площадью именно квадрат имеет наимень- |
|||||||
ший периметр. |
|
|
|
|
|
||
2. Обобщение на случай n переменных. Неравенство (1), связывающее средние арифметическое и геометрическое двух положительных величин, может быть обобщено на любое число n положительных величин, которые мы будем обозначать x1, x2, x3, . . . , xn. Средним арифметическим этих величин называют выражение
m = x1 + x2 + . . . + xn , n

§ 6 |
ЭКСТРЕМУМЫ И НЕРАВЕНСТВА |
391 |
а средним геометрическим — выражение
√
g = n x1x2 . . . xn,
причем имеется в виду всегда положительное значение радикала. Общая теорема утверждает, что
g 6 m |
(2) |
и что равенство g = m возможно только в том случае, если все величины xi равны между собой.
Было предложено много различных остроумных доказательств этого общего результата. Простейший метод заключается в применении того же простого рассуждения, которое мы провели в пункте 1. Перед нами стоит проблема: разбить данное положительное число C на n положительных слагаемых, C = x1 + x2 + . . . + xn, таким образом, чтобы произведение P = x1x2 . . . xn было возможно большим. Мы будем исходить из допущения, на первый взгляд очевидного, но мы позднее будем иметь случай его проанализировать (§ 7), что наибольшее значение P существует и достигается, скажем, при значениях x1 = a1, x2 = a2, . . . , xn = an. Нам достаточно установить, что a1 = a2 = . . . = an, ибо в этом случае g = m. Допустим, что это не так: пусть, например, a1 6= a2. Тогда рассмотрим значения
x1 = s, x2 = s, x3 = a3, . . . , xn = an,
где
s = a1 + a2 .
2
Другими словами, мы заменим прежнюю систему значений величин xi новой системой, которая отличается от прежней лишь тем, что значения двух первых величин x1 и x2 сделаны равными между собой, причем общая сумма C остается неизменной. Мы можем написать
a1 = s + d, a2 = s − d,
где положено
d = a1 − a2 .
2
Новое произведение равно
P 0 = s2 · a3 . . . an,
тогда как прежнее произведение было
P = (s + d)(s − d) · a3 . . . an = (s2 − d2) · a3 . . . an.
Отсюда ясно, что при d 6= 0
P< P 0,
аэто противоречит сделанному допущению, что произведение P имеет максимальное значение. Итак, d = 0, и тогда a1 = a2. Таким же образом

392 |
МАКСИМУМЫ И МИНИМУМЫ |
гл. VII |
доказывается, что a1 = ai, где ai обозначает любое из чисел a; отсюда следует, что все числа a равны между собой. Мы убедились в том, что 1) g = m, если все числа xi равны между собой, 2) наибольшее значение g получается только тогда, когда все числа xi равны между собой. Отсюда можно заключить, что во всех прочих случаях g < m. Теорема доказана.
3. Метод наименьших квадратов. Среднее арифметическое n
чисел x1, x2, . . . , xn (которые здесь нет необходимости считать обязательно положительными) обладает замечательным минимальным свойством. Пусть u — числовое значение некоторой неизвестной величины, которое мы хотим определить насколько возможно точнее с помощью какого-то измерительного инструмента. Пусть произведено для этой цели n измерений, которые дали результаты x1, x2, . . . , xn, слегка различающиеся между собой, что обусловливается неизбежными и зависящими от разных причин измерительными ошибками. Возникает вопрос: какое же значение следует приписать величине u в качестве заслуживающего наибольшего доверия? В качестве «истинного» или «оптимального» значения принято выбирать среднее арифметическое
m = x1 + x2 + . . . + xn . n
Дать подлинное обоснование указанной процедуре было бы невозможно, не углубляясь в пространные рассуждения, относящиеся к области теории вероятностей. Все же мы можем здесь отметить некоторое минимальное свойство средней арифметической m, которое до некоторой степени оправдывает ее выбор. Пусть u — какое угодно числовое значение измеряемой величины. Тогда разности u − x1, u − x2, . . . , u − xn представляют собой отклонения этой величины от результатов отдельных наблюдений. Эти отклонения могут быть частью положительными, частью отрицательными, и совершенно естественно стремиться к такому оптимальному выбору u, при котором «тотальное» (в каком-то смысле) отклонение было бы возможно меньше. Следуя Гауссу, берут обыкновенно в качестве «измерителей неточности» не сами отклонения, а их квадраты (u − xi)2 и затем выбирают оптимальное значение u с таким расчетом, чтобы минимизировать «тотальное» отклонение, под каковым понимают сумму квадратов отдельных отклонений
(u − x1)2 + (u − x2)2 + . . . + (u − xn)2.
Определенное таким образом оптимальное значение u есть не что иное, как среднее арифметическое m: в этом заключается исходное положение знаменитого «метода наименьших квадратов», созданного Гауссом. Мы постараемся возможно проще доказать это утверждение. Если мы напишем
(u − xi) = (m − xi) + (u − m),
§ 6 |
ЭКСТРЕМУМЫ И НЕРАВЕНСТВА |
393 |
то получим
(u − xi)2 = (m − xi)2 + (u − m)2 + 2(m − xi)(u − m).
Сложим, далее, все такие равенства, полагая i = 1, 2, . . . , n. Последний член при этом дает
2(u − m)(nm − x1 − . . . − xn),
а это выражение по определению m равно нулю. Следовательно, мы получаем:
(u − x1)2 + (u − x2)2 + . . . + (u − xn)2 =
= (m − x1)2 + (m − x2)2 + . . . + (m − xn)2 + n(u − m)2.
Отсюда уже ясно, что
(u − x1)2 + (u − x2)2 + . . . + (u − xn)2 >
> (m − x1)2 + (m − x2)2 + . . . + (m − xn)2,
причем знак равенства возможен только при u = m. Как раз это самое мы и собирались доказать.
Общий метод наименьших квадратов принимает руководящий принцип — минимизировать сумму квадратов — во всех более сложных случаях, когда нужно как-то согласовать между собой ряд слегка противоречащих друг другу данных наблюдения. Так, представим себе, что измерены координаты xi, yi для n точек, которые теоретически должны лежать на прямой линии, и предположим, что полученные таким эмпирическим путем точки оказываются расположенными по прямой не вполне точно. Как выбрать прямую, которая наилучшим образом была бы «приложена» или «подогнана» к этим точкам? Руководящий принцип приводит к следующему приему (который — необходимо признать — мог бы быть заменен и другими процедурами, основанными на иных рассуждениях). Пусть y = ax + b есть уравнение искомой прямой, так что наша проблема заключается в определении коэффициентов a и b. Измеренное по направлению оси y расстояние прямой от точки xi, yi равно yi − (axi + b), т. е. yi − axi − b, причем имеет положительный или отрицательный знак, смотря по тому, расположена ли точка выше или ниже прямой. Тогда квадрат этого расстояния равен (yi − axi − b)2, и согласно основному принципу метода наименьших квадратов нам достаточно подобрать a и b таким образом, чтобы выражение
(y1 − ax1 − b)2 + (y2 − ax2 − b)2 + . . . + (yn − axn − b)2
достигало наименьшего возможного значения. Мы приходим, таким образом, к минимальной проблеме с двумя переменными величинами a и b. Хотя решение этой проблемы с исследованием всех подробностей и не представляет особенной трудности, мы все же воздержимся здесь от его рассмотрения.
